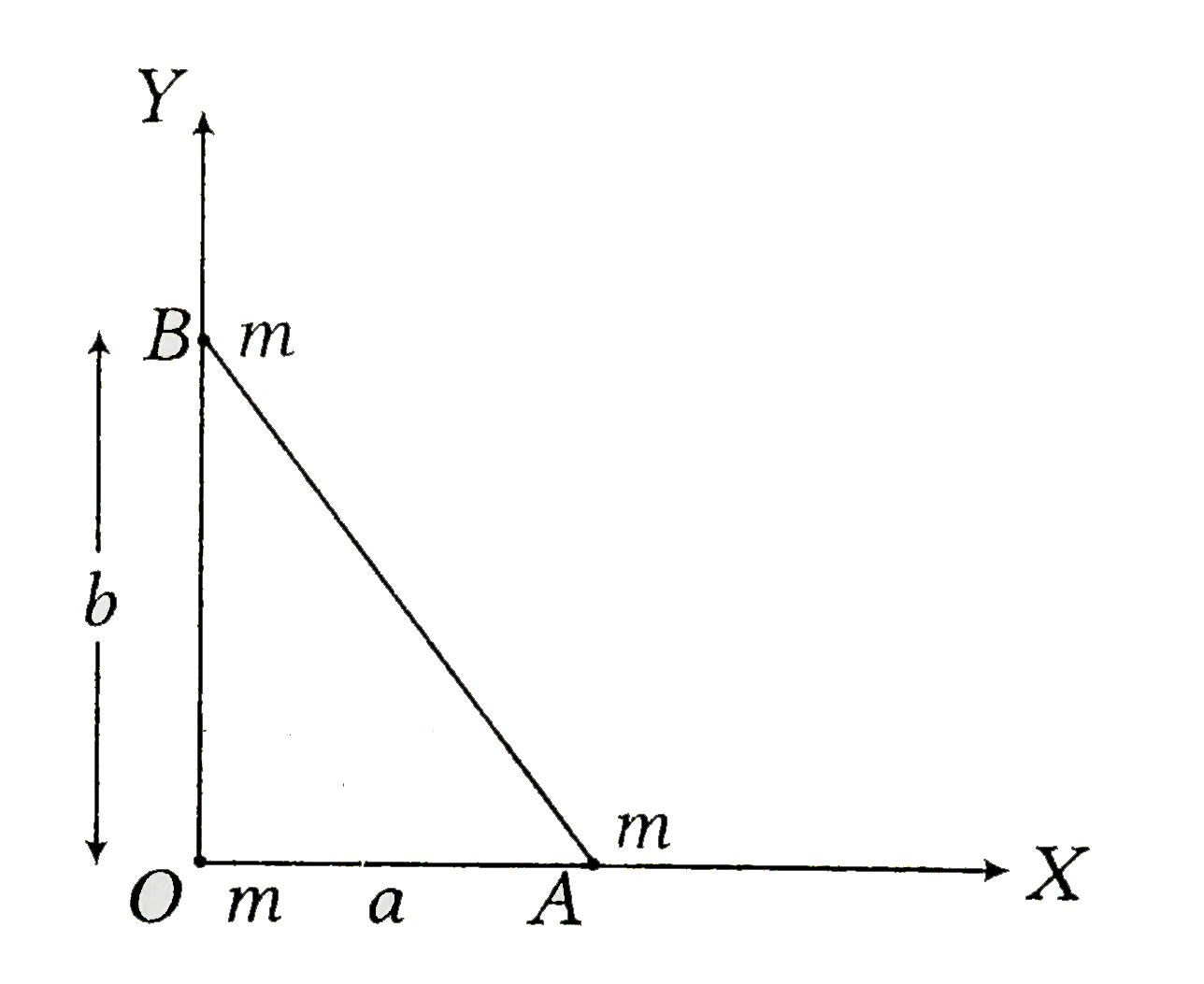
Locate the centre of mass of a system of three particles 1,2 and 3 each of mass m situated at the vertices of a right angled triangle as shown in figure.

The correct Answer is:→rcm=7l12ˆi+√312ˆj
Similar Questions
The position co-ordinates of the centre of mass of a system of three particles of equal masses which are placed on the verctices of an equilateral triangle of a side a are shown. Locate centre mass?

View SolutionThe position co-ordinates of the centre of mass of a system of three particles of equal masses which are placed on the verctices of an equilateral triangle of a side a are shown. Locate centre mass?

View Solution
Knowledge Check
Three particles , each of mass m, are placed at the vertices of a right angled triangle as shown in figure. The position vector of the center of mass of the system is (O is the origin and ˆi,ˆj,ˆk are unit vectors)
 A13(aˆi−bˆj)B23(aˆi−bˆj)C23(aˆi+bˆj)D13(aˆi+bˆj)
A13(aˆi−bˆj)B23(aˆi−bˆj)C23(aˆi+bˆj)D13(aˆi+bˆj)The gravitational potential energy of a system of three particles of mass m each kept at the vertices of equilateral triangle of side x will be
A−Gm2xB−Gm23xC−3Gm2xD3Gm2x2
Three charges +q,−q,and+2q are placed at the verticles of a right angled triangle (isoceles triangle) as shown. The net electrostatic energy of the configuration is :

View SolutionFind centre of mass of a system of three particle kept at the corner equilateral triangle as shown in figure
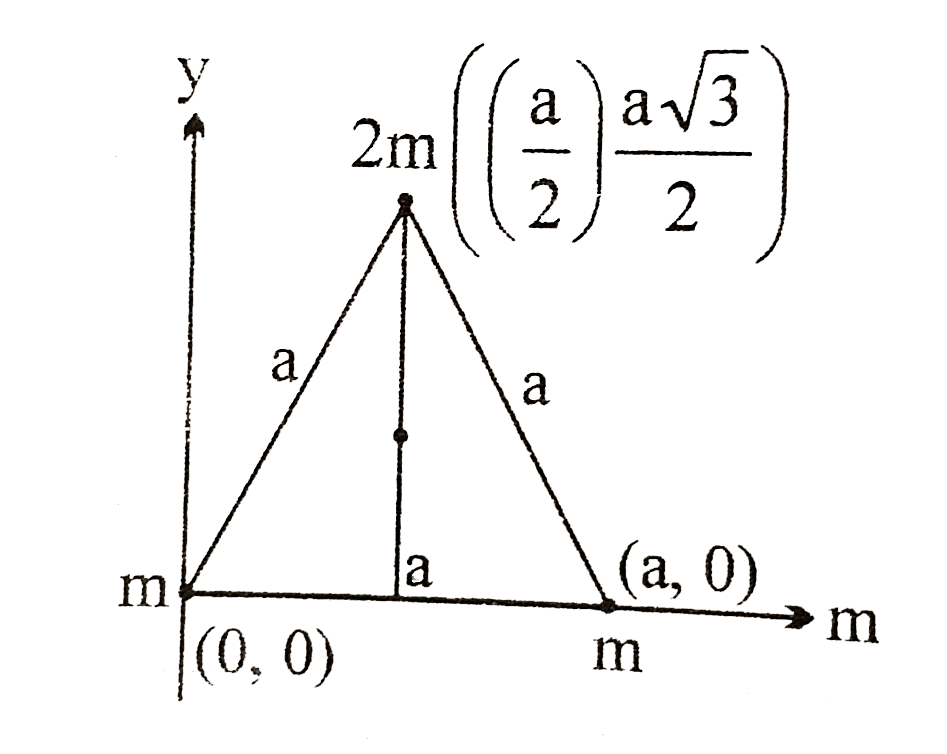
View SolutionThe gravitational potential energy of a system of three particles of mass m each kept at the vertices of equilateral triangle of side x will be
View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side L as shown in the figure. Find the moment of inertia of the system about the line AX perpendicular to AB in the plane of ABC

View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side l (as shown in the figure).
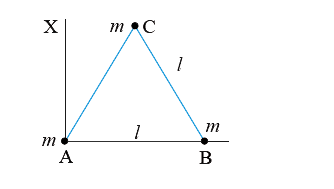
The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, will be:
View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side l (as shown in the figure).

The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, will be:
View Solution
