Two rods of different metals, having the same area of cross-section A, are placed end to end between two massive walls as shown in fig. If the temperature of both the rods are now raised by Δt0C then
(a) Find the force with which the rods acts on cach other at higher temperature.
(b) Find the lengths of the rods at the higher temperature.
Assume that there is no change in the cross-sectional area of the rods and the rods do not bend. There is no deformation of walls.

(a) Due to heating the increases in length of the composite rod will be (Δl)1=l1α1Δt+l2α2Δt=(l1α1+l2α2)Δt...(1)
due to compressive force .F from the walls, due to elasticity, the decrease in length will be
(Δl)D=Fl1AY1+Fl2AY2=FA(l1Y1+l2Y2)....(2)
As the length of the composite rod remains unchanged the increase in length due to heating must be equal to decrease in length due to compression.
(l1α1+l2α2)Δ=FA(l1Y1+l2Y2)⇒(##AKSELTAIPHYXIV01C_C01SLV023_S01.png width=80%><br>As∈itiallythe≤n>hofo≠rod∈L,anddue→heat∈gits≤n>h∈creasesby(Deltal_(1))_(H)=alpha_(1) l_(1)Deltat.<br>whi≤due→compressionits≤n>hdecreasesby(Deltal_(1_(C))=(Fl_(1))/(AY_(1))<br>soitsf∈al≤n>hl_(1)^(1)=l_(1)+(Deltal_(1))_(H)-(Deltal_(1))_(C)=l_(1)+l_(1)alpha_(1) Deltat-(Fl_(1))/(AY_(1))<br>fortheotherfordl_(1)^(2)=l_(2)+(Deltal_(2))_(H)-(Deltal_(2))_(C), l_(2)^(1)=l_(2)+l_(2)alpha_(2)Deltat-(Fl_(2))/(AY_(2))
Topper's Solved these Questions
- ELASTICITYBOOK - AAKASH SERIESCHAPTER - ELASTICITYEXERCISE - TEST YOUR SELF
11 Videos
- ELASTICITYBOOK - AAKASH SERIESCHAPTER - ELASTICITYEXERCISE - Very Short Answer Type Questions
15 Videos
- COLLISIONS BOOK - AAKASH SERIESCHAPTER - COLLISIONS EXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
4 Videos
- ELEMENTS OF VECTORS BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORS EXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWER
10 Videos
Similar Questions
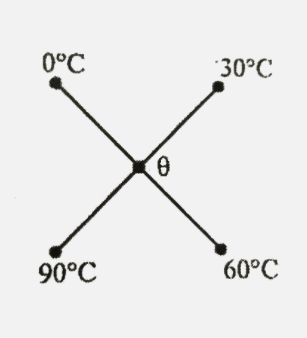
Three rods of same material and of equal cross sectional area and length have been connected together as shown in the figure. The temperature of the junction of the rods approximately is
View SolutionFour rods of same material and having the same cross section and length have been joined, as shown. The temperature of the junction of four rods will be :
View Solution
Knowledge Check
In the steady state the two ends of a meter rod are at 30∘C and 20∘C the temperature at the 40thcm from the end at higher temperature is .
A22∘CB26∘CC25∘CD24∘CTwo rods of different materials having differnet lengths and same cross sectional areas are joined end to end in a straight line. The free ends of this compound rod are maintained at different temperatures The temperature gradient in each rod will be .
AsameBzeroCdirectly proportional to thermal conductivity of rodDinversely proportional to thermal conductivity of the rod .Assertion A metallic rod is fixed from two ends as shown in figure. When the temperature is increased compressive stresses are developed in the rod.
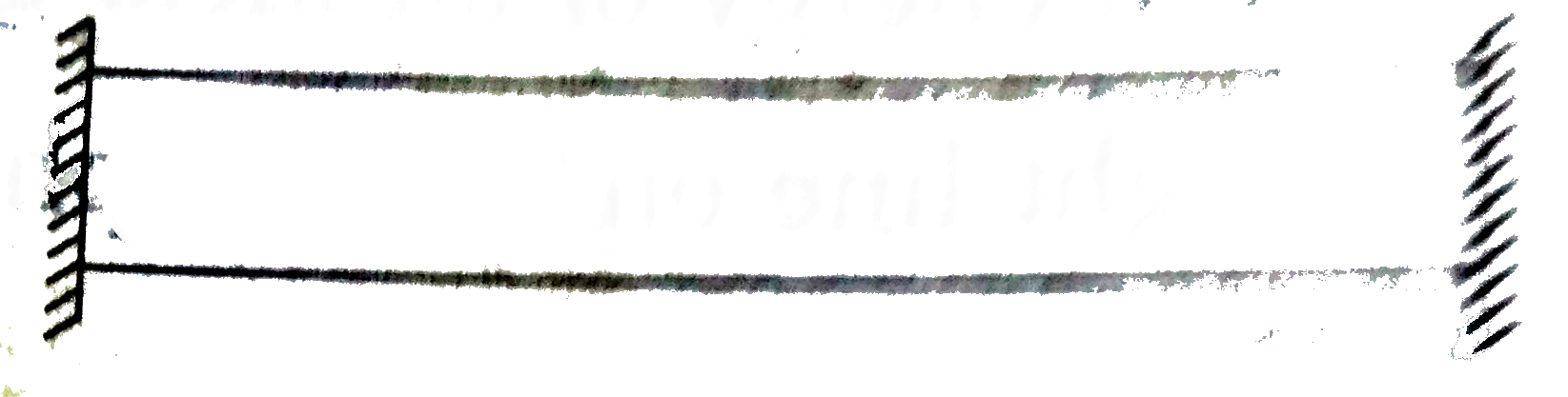
Reason At higher temperature, natural length of the rod will be more.AIf both Assertion and Reason are correct and Reason is the correct explanation of Assertion.BIf both Assertion and Reason are correct but Reason is not the correct explation os Assertion.CIf Assertionis true bur Reason is false.DIf Assertion is false but Reason is true.
Two rods of different metals having the same area of cross section A are placed between the two massive walls as shown is Fig. The first rod has a length l1, coefficient of linear expansion α1 and Young's modulus Y1. The correcsponding quantities for second rod are l2,α2 and Y2. The temperature of both the rods is now raised by t∘C.
i. Find the force with which the rods act on each other (at higher temperature) in terms of given quantities.
ii. Also find the length of the rods at higher temperature.

View SolutionTwo rods of different metals having the same area of cross section A are placed between the two massive walls as shown is Fig. The first rod has a length l1, coefficient of linear expansion α1 and Young's modulus Y1. The correcsponding quantities for second rod are l2,α2 and Y2. The temperature of both the rods is now raised by t∘C.
i. Find the force with which the rods act on each other (at higher temperature) in terms of given quantities.
ii. Also find the length of the rods at higher temperature.

View SolutionTwo rods of different metals having the same area of cross section A are placed between the two massive walls as shown is Fig. The first rod has a length l1, coefficient of linear expansion α1 and Young's modulus Y1. The correcsponding quantities for second rod are l2,α2 and Y2. The temperature of both the rods is now raised by t∘C.
i. Find the force with which the rods act on each other (at higher temperature) in terms of given quantities.
ii. Also find the length of the rods at higher temperature.

View SolutionAssertion A metallic rod is fixed from two ends as shown in figure. When the temperature is increased compressive stresses are developed in the rod.
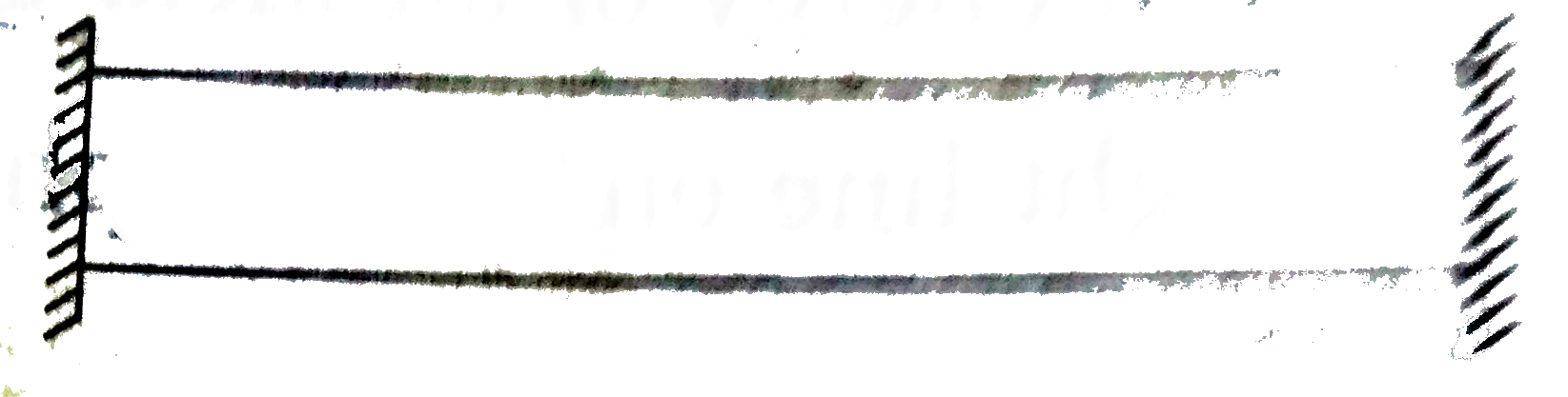
Reason At higher temperature, natural length of the rod will be more.
View SolutionThree rods A,B and C of the same length and cross- sectional area are joined in series as shown. The temperature at the junction of A and B, in equilibriu, is
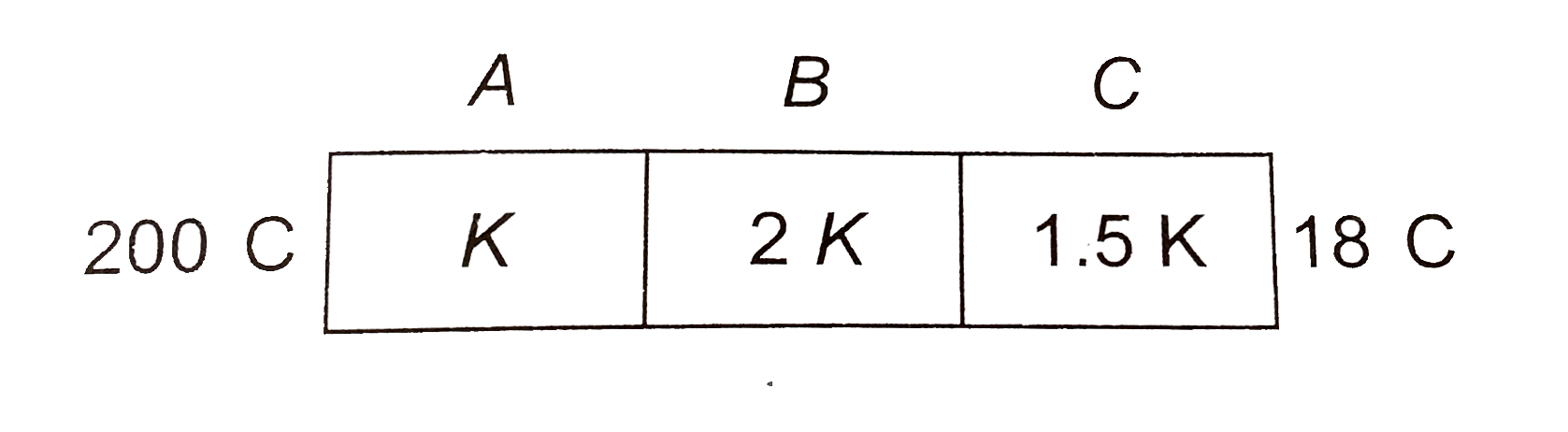
View Solution
