A circular disc of diameter d and a square plate of side d are placed as shown in fig. The centre of mass of this combination from centre of disc is (both the object are having same mass per unit area):
4d4+π
4d3+π
2d+3π4+π
3d+7π4+π
The correct Answer is:A
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - SYSTEM OF PARTICLES AND ROTATIONAL MOTION (MOMENT OF INTERTIA)18videos
APPENDICES
- BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - SYSTEM OF PARTICLES AND ROTATIONAL MOTION (CONSERVATION OF ANGULAR MOMENTUM)7videos
APPENDICES
- BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - WORK POWER ENERGY (SCALAR OR DOT PRODUCT) (COLLISIONS)26videos
APPENDICES
- BOOK - AAKASH SERIESCHAPTER - CALORIMETRY EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) (LECTURE SHEET (ADVANCED)(Matrix Type Questions)1videos
CALORIMETRY
Similar Questions
A square plate of edge d and a circular disc of diameter d are placed toucing ech other at the midpoint of san edge of th plate as shown in figure. Locate the centre of mass of the combination assuming same mass per unit area for the two plates.
View SolutionA square plate of edge d and a circular disc of diameter d are placed toucing ech other at the midpoint of san edge of th plate as shown in figure. Locate the centre of mass of the combination assuming same mass per unit area for the two plates.
View Solution
Knowledge Check
- Question 1 - Select One
A square plate of edge d and a circular disc of diameter d are placed touching each other at the midpoint of an edge of plate as shown. Then center of mass of the combination will be (assume same mass per unit area for the two plates):
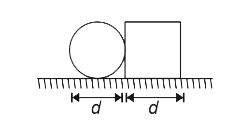A2d2+π left to the center of the discB2d2+π right to the center of the discC4d4+π right to the center of the discD4d4+π left to the center of the disc - Question 2 - Select One
A circular disc of radius R is removed from a bigger of the discs coincide. The centre of mass of the new disc is ar from the centre of the bigger disc. The value of α is
A14B13C12D16 - Question 3 - Select One
In the figure one fourth part of a uniform disc of radius R is shown. The distance of the centre of mass of this object from centre 'O' is :
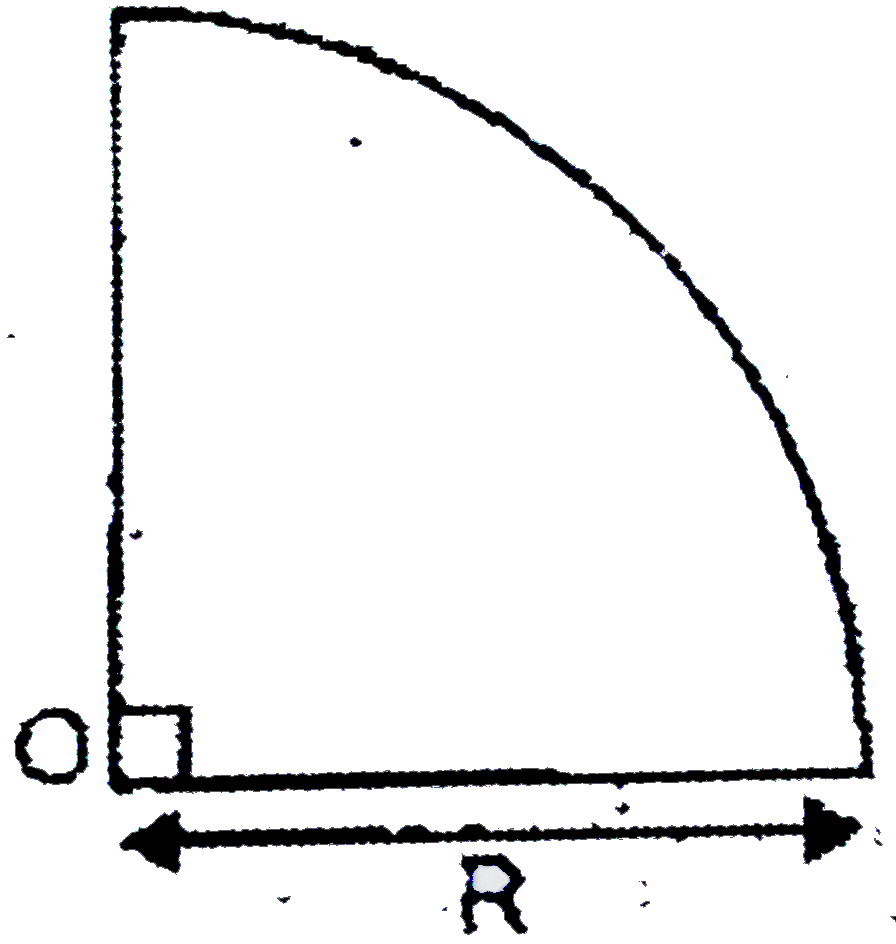A4R3πB2r3πC√24R3πD√22R3π
From a circular disc of radius R, a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is −
View SolutionA circular plate of diameter d is kept in contact with a square plate of edge d as shown in figure. The densit of the material and the thickness are same
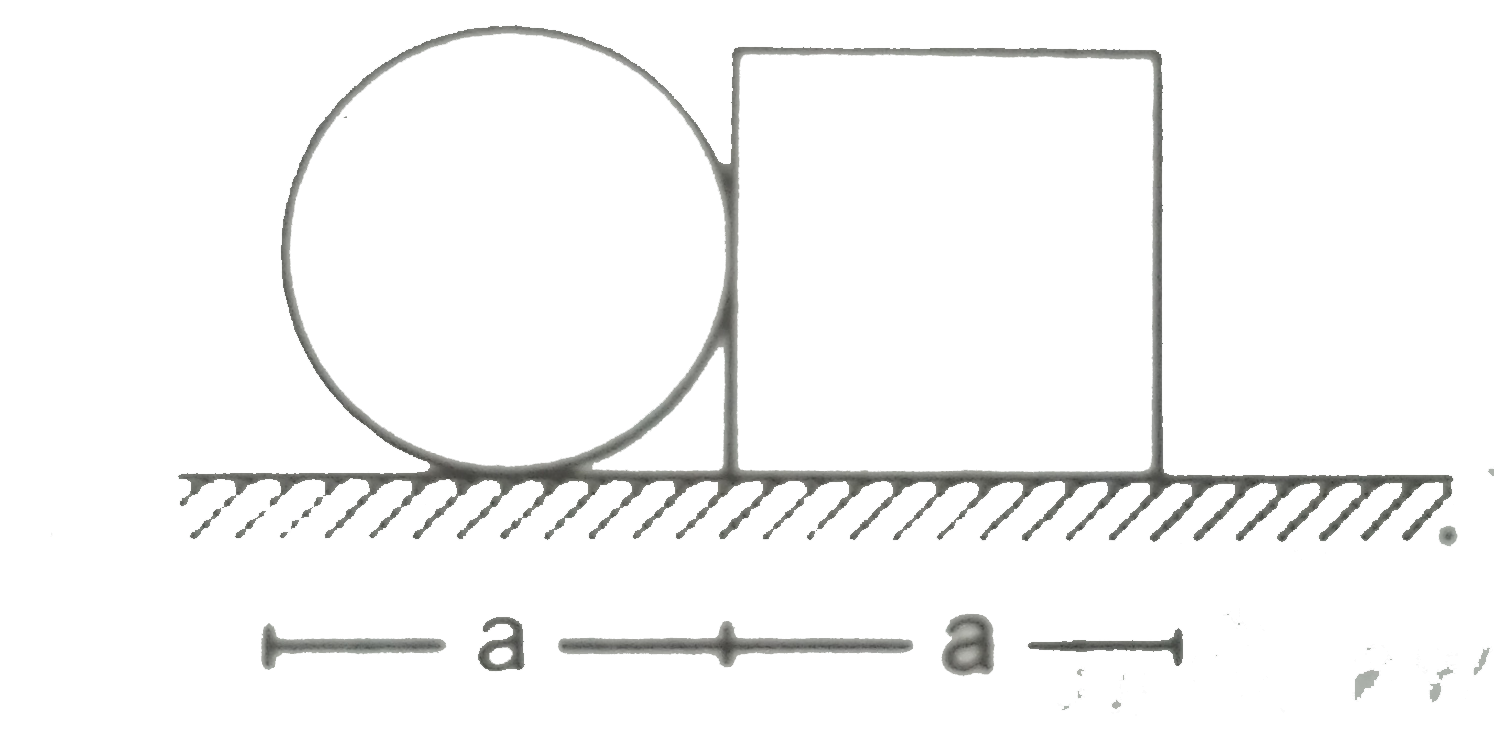. Everywhere. The centre of mass of the composite system will be View SolutionA circular plate of diameter d is kept in contact with a square plate of edge d as shown in figure. The densit of the material and the thickness are same
. Everywhere. The centre of mass of the composite system will be View SolutionFrom a circular disc of radius R, a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is −
View SolutionA circular plate of diameter d is kept in contact with a square plate of edge d as shown in figure. The densities of the material and the thickness are same
. Everywhere. The centre of mass of the composite system will be View Solution