A uniform square sheet has a side length of 2R. A circular sheet of maximum possible area is removed from one of the quadrants of the square sheet. The distance of centre of mass of the remaining portion from the centre of the original sheet is
πR√2[16−π]
R[16−π]
Rπ[16−π]
Rπ16−π
The correct Answer is:A
Topper's Solved these Questions
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - SYSTEM OF PARTICLES AND ROTATIONAL MOTION (MOMENT OF INTERTIA)
18 Videos
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - SYSTEM OF PARTICLES AND ROTATIONAL MOTION (CONSERVATION OF ANGULAR MOMENTUM)
7 Videos
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - WORK POWER ENERGY (SCALAR OR DOT PRODUCT) (COLLISIONS)
26 Videos
- CALORIMETRY BOOK - AAKASH SERIESCHAPTER - CALORIMETRY EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) (LECTURE SHEET (ADVANCED)(Matrix Type Questions)
1 Video
Similar Questions
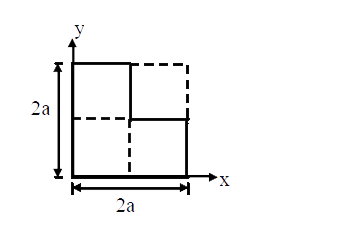
A square of side 4m having uniform thickness is divided into four equal squares as shown in Fig. If one of the squares is cut off, find

the position of centre of mass of the remaining portion from the centre O.
View SolutionIn the figure shown a semicircular area is removed from a uniform square plate of side l and mass ‘m’ (before removing). The x-coordinate of centre of mass of remaining portion is (The origin is at the centre of square)
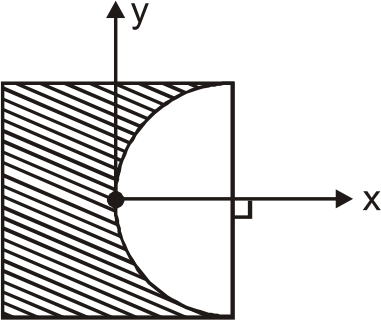
View Solution
Knowledge Check
Figure shows a square plate of uniform thickness and side length √2m. One fourth of the plate is removed as indicated. The distance of centre of mass of the remaining portion from the centre of the original square plate is
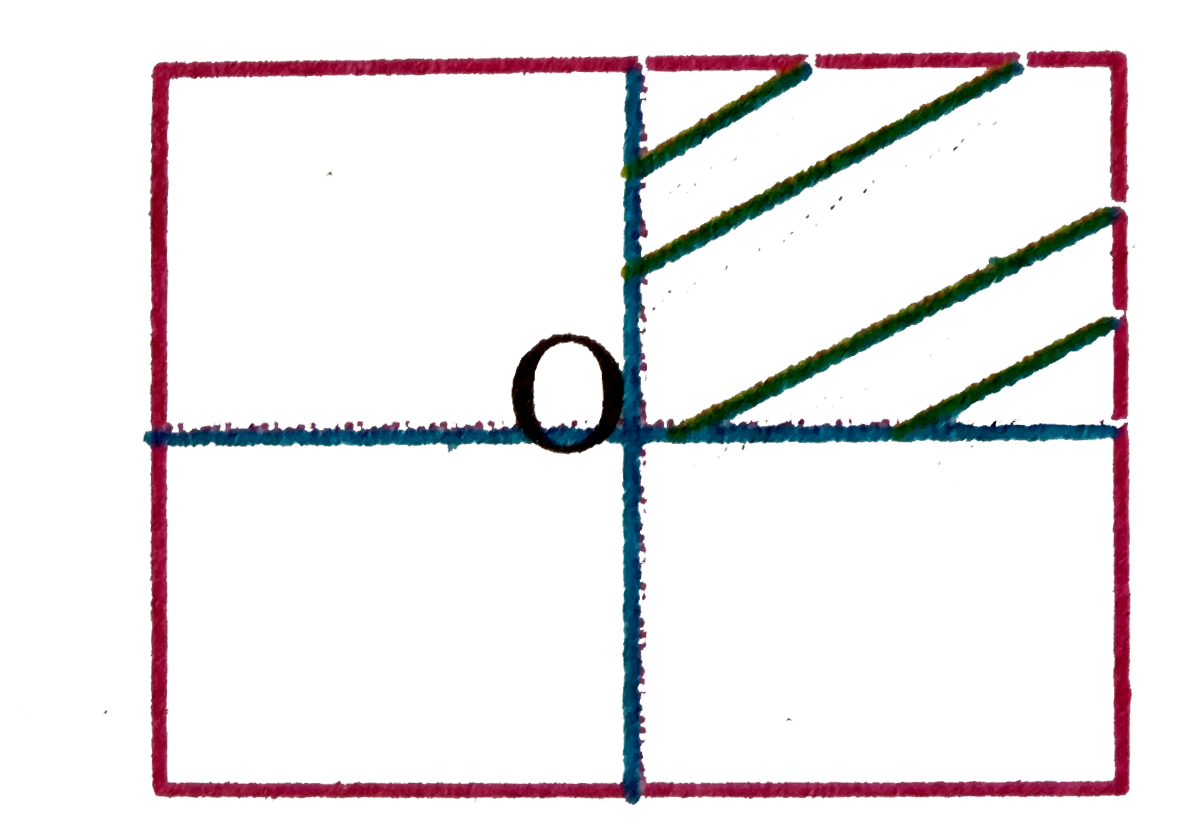 A1/3mB1/2mC1/6mD1/8m
A1/3mB1/2mC1/6mD1/8mThe side of a square metal sheet is 7 m. A circular sheet of maximum radius is cut and removed. Find the area of the circular sheet (in ft2).
 A49πB49π2C49π4D49π8
A49πB49π2C49π4D49π8In the figure shown a semicircular area is removed from a uniform square plate of side l and mass ‘m’ (before removing). The x-coordinate of centre of mass of remaining portion is (The origin is at the centre of square)
 A−π(π−2)l2(8−π)Bπ(π−2)l2(8−π)C−π(π−2)l8−πD−l(π−43)2(8−π)
A−π(π−2)l2(8−π)Bπ(π−2)l2(8−π)C−π(π−2)l8−πD−l(π−43)2(8−π)
Find the position of centre of mass of the uniform planner sheet shown in figure with respect to the origin (O) -
View SolutionFrom a square sheet of uniform density , a portion a removed shown shaded in fig. Find the centre of msas of the remaining portion is the side of the square is α

View SolutionFrom a uniform circular disc of radius R, a circular disc of radius R/6 and having centre at a distance R/2 from the centre of the disc is removed. Determine the centre of mass of remaining portion of the disc.
View SolutionFour identical strips in the form of right isosceles triangles are removed from the four corners of a square sheet of side 8 cm. Find the area of the remaining sheet, if the length of each, equal sides of the triangles is 4 cm,
View SolutionA uniform circular disc of radius a is taken. A circular portion of radius b has been removed from it as shown in the figure. If the center of hole is at a distance c from the center of the disc, the distance x2 of the center of mass of the remaining part from the initial center of mass O is given by

View Solution
