A square plate of edge d and a circular disc of diameter d are placed toucing ech other at the midpoint of san edge of th plate as shown in figure. Locate the centre of mass of the combination assuming same mass per unit area for the two plates.
To locate the center of mass of the combination of a square plate and a circular disc, we can follow these steps:
Step 1: Define the Geometry
- We have a square plate of edge length d and a circular disc with a diameter d placed such that it touches the midpoint of one edge of the square plate.
- The square plate can be positioned such that its bottom left corner is at the origin (0,0) and its center is at (d2,d2).
- The circular disc, touching the midpoint of the square plate's edge, has its center at (d2,0).
Step 2: Calculate the Areas
- The area of the square plate As is given by:
As=d2
- The radius r of the circular disc is d2, so its area Ac is:
Ac=π(d2)2=πd24
Step 3: Calculate the Masses
Assuming the same mass per unit area σ for both shapes:
- The mass of the square plate ms is:
ms=σAs=σd2
- The mass of the circular disc mc is:
mc=σAc=σ⋅πd24
Step 4: Find the Coordinates of the Centers of Mass
- The center of mass of the square plate is at (d2,d2).
- The center of mass of the circular disc is at (d2,0).
Step 5: Apply the Center of Mass Formula
The coordinates of the center of mass (xcm,ycm) of the system can be calculated using the formula:
xcm=msxs+mcxcms+mc
ycm=msys+mcycms+mc
Substituting the values:
- For xcm:
xcm=ms⋅d2+mc⋅d2ms+mc=(σd2⋅d2)+(σ⋅πd24⋅d2)σd2+σ⋅πd24
This simplifies to:
xcm=d32σ+πd38σσd2(1+π4)=d3(4+π8)d2(1+π4)=d(4+π)8+2π
- For ycm:
ycm=ms⋅d2+mc⋅0ms+mc=σd2⋅d2σd2+σ⋅πd24=d32d2(1+π4)=d2(1+π4)
Final Result
Thus, the center of mass of the combination is located at:
(d(4+π)8+2π,d2(1+π4))
- We have a square plate of edge length d and a circular disc with a diameter d placed such that it touches the midpoint of one edge of the square plate.
- The square plate can be positioned such that its bottom left corner is at the origin (0,0) and its center is at (d2,d2).
- The circular disc, touching the midpoint of the square plate's edge, has its center at (d2,0).
- The area of the square plate As is given by:
As=d2
- The radius r of the circular disc is d2, so its area Ac is:
Ac=π(d2)2=πd24
Assuming the same mass per unit area σ for both shapes:
- The mass of the square plate ms is:
ms=σAs=σd2
- The mass of the circular disc mc is:
mc=σAc=σ⋅πd24
- The center of mass of the square plate is at (d2,d2).
- The center of mass of the circular disc is at (d2,0).
The coordinates of the center of mass (xcm,ycm) of the system can be calculated using the formula:
xcm=msxs+mcxcms+mc
ycm=msys+mcycms+mc
Substituting the values:
- For xcm:
xcm=ms⋅d2+mc⋅d2ms+mc=(σd2⋅d2)+(σ⋅πd24⋅d2)σd2+σ⋅πd24
This simplifies to:
xcm=d32σ+πd38σσd2(1+π4)=d3(4+π8)d2(1+π4)=d(4+π)8+2π
ycm=ms⋅d2+mc⋅0ms+mc=σd2⋅d2σd2+σ⋅πd24=d32d2(1+π4)=d2(1+π4)
Thus, the center of mass of the combination is located at:
(d(4+π)8+2π,d2(1+π4))
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective 2
11 Videos
- CALORIMETRYBOOK - HC VERMACHAPTER - CALORIMETRYEXERCISE - Exercises
18 Videos
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Exercises
30 Videos
Similar Questions
A circular plate of unifrom thickness has a diameter of 56cm. A circular portion of diameter 42cm is removed from the edge of the plate as shown in Fig. Find the position of centre of mass of the remaining portion.
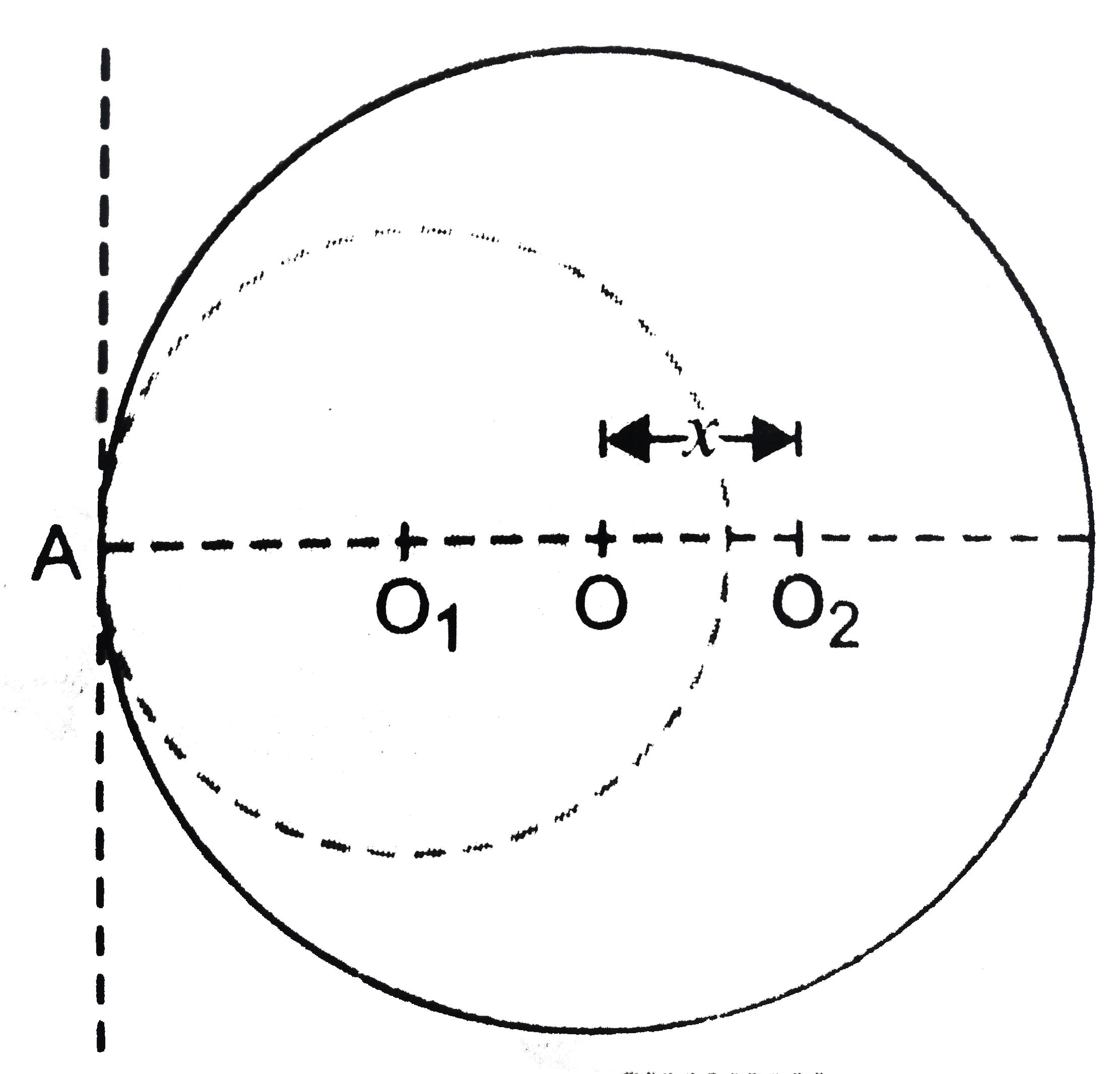
View SolutionA circular plate of unifrom thickness has a diameter of 56cm. A circular portion of diameter 42cm is removed from the edge of the plate as shown in Fig. Find the position of centre of mass of the remaining portion.

View Solution
Knowledge Check
A square plate of edge d and a circular disc of diameter d are placed touching each other at the midpoint of an edge of plate as shown. Then center of mass of the combination will be (assume same mass per unit area for the two plates):
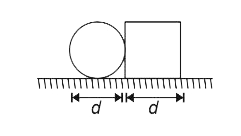 A2d2+π left to the center of the discB2d2+π right to the center of the discC4d4+π right to the center of the discD4d4+π left to the center of the disc
A2d2+π left to the center of the discB2d2+π right to the center of the discC4d4+π right to the center of the discD4d4+π left to the center of the discFive uniform circular plates, each of diameter b and mass m are laid out in a pattern shown. Using the origin shown, find the y co-ordinate of the centre of mass of the five-plate system.
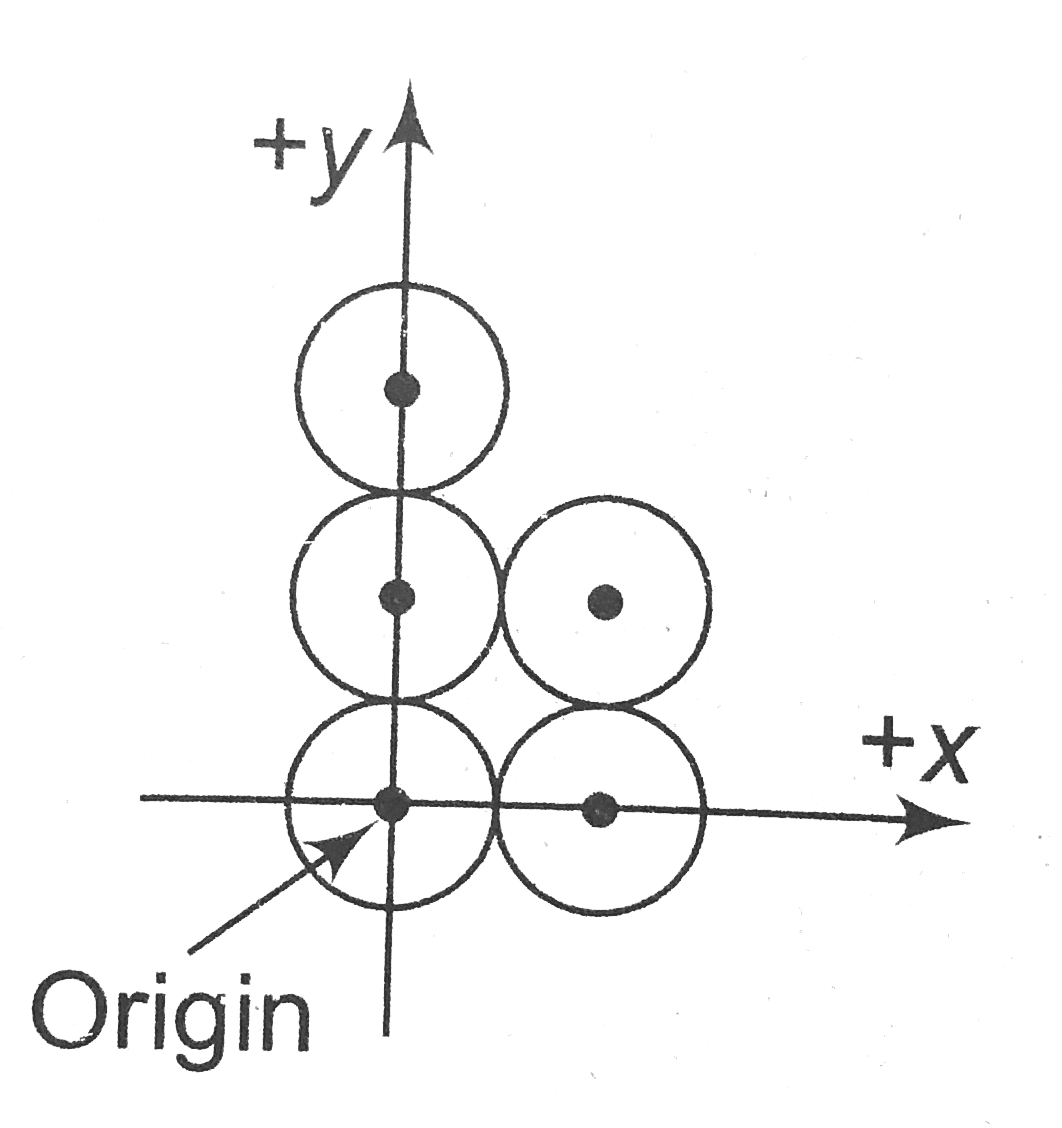 .Ab/5Bb/3C4b/5D2b/5
.Ab/5Bb/3C4b/5D2b/5A square plate of side 20cm has uniform thickness and density. A circular part of diameter 8cm is cut out symmetrically and shown in figure. The position of center of mass of the remaining potion is
 Aat O1Bat OC0.54 cm from O on the left hand sideDNone of the above
Aat O1Bat OC0.54 cm from O on the left hand sideDNone of the above
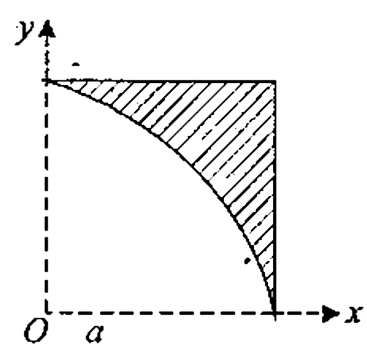
Fron a sqaure plate of side a,a quarter circular disc of radius a is removed as shown in figure. Find the coordinates of centre of mass of the remaining part.
View SolutionHalf of the recrtangular plate shown in figure is made of a material of density ρ1 and the other half of density ρ2. The length of the plate is L. Locate the centre of mass of the plate.

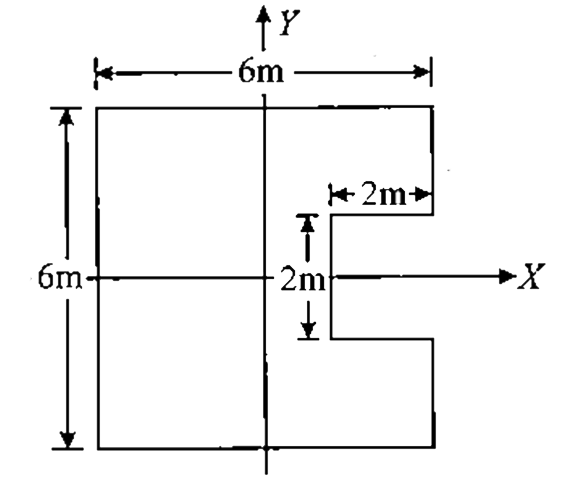
View SolutionFind x and y coordinats of the centre of mass of the plate shown in figure from which a square of side 2 m is cut out.
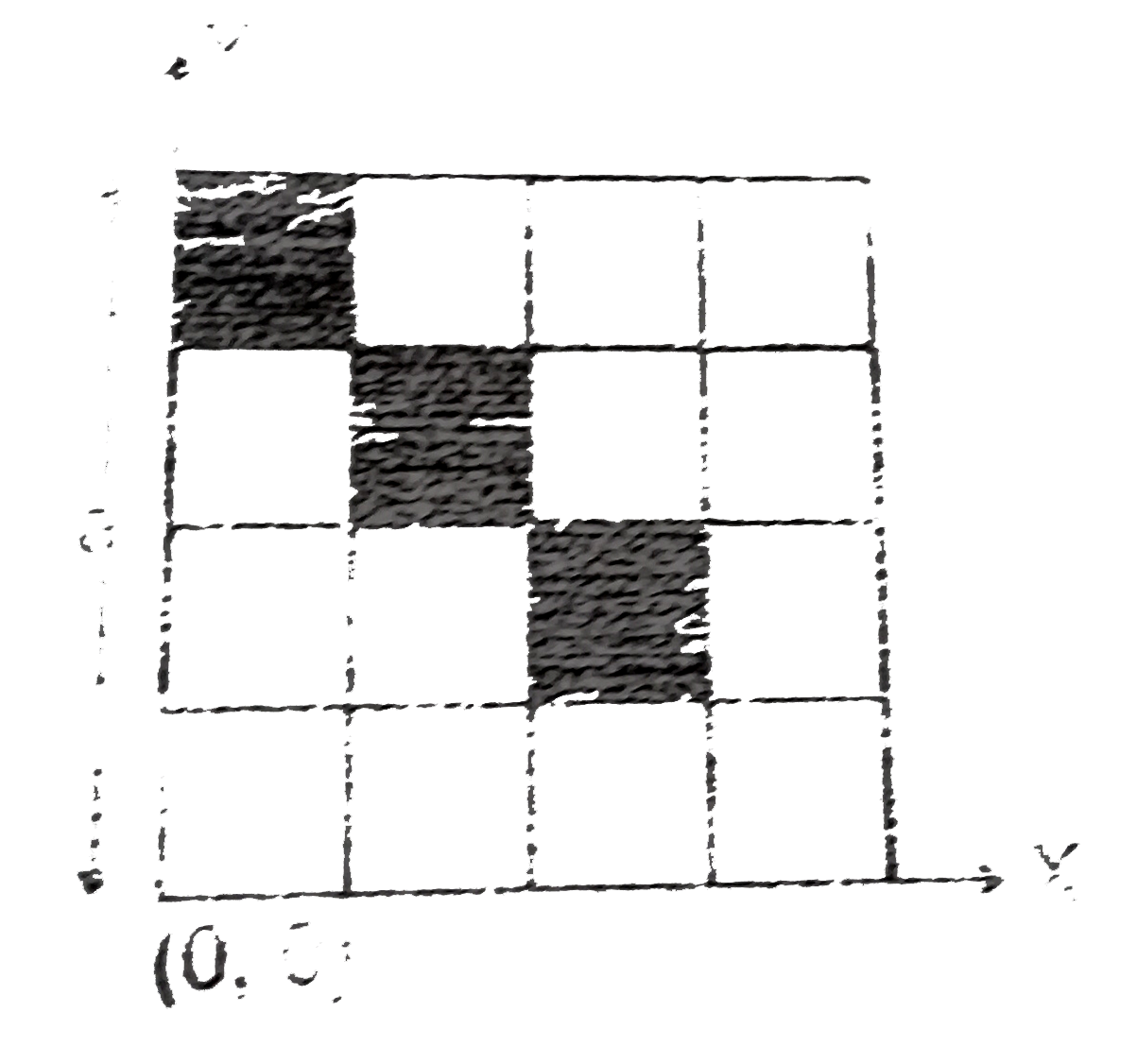
View SolutionFrom a uniform square plate the shaped portions are removed as shown in figure. The coordinates of centre of mass of the remaining plate are x,y Axes and origon are shown in figure.
View SolutionA circular plate of diameter d is kept in contact with a square plate of edge d as shown in figure. The densities of the material and the thickness are same
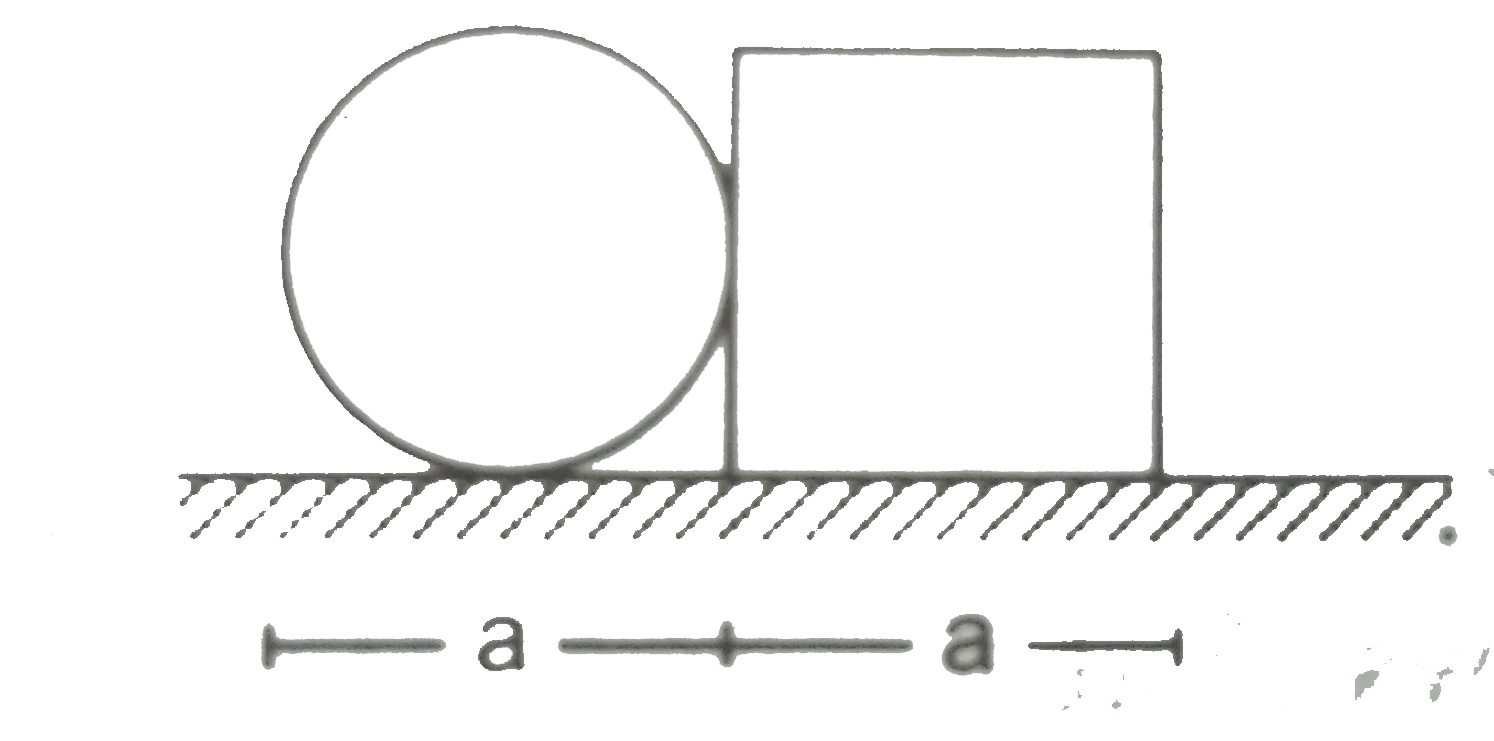 . Everywhere. The centre of mass of the composite system will be
. Everywhere. The centre of mass of the composite system will be
View Solution
