In a rectangle ABCD, AB - 2l and BC =l. The centre of rectangle is at the origin of co-ordinate system. AB and CD are parallel to X-axis. The M.I. is least about
A
BD
B
BC
C
X-axis
D
Y-axis
Text Solution
The correct Answer is:C
|
Topper's Solved these Questions
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - SYSTEM OF PARTICLES AND ROTATIONAL MOTION (CONSERVATION OF ANGULAR MOMENTUM)
7 Videos
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - SYSTEM OF PARTICLES AND ROTATIONAL MOTION (ROTATIONAL DYNAMICS)
26 Videos
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - SYSTEM OF PARTICLES AND ROTATIONAL MOTION (CENTRE OF MASS)
36 Videos
- CALORIMETRY BOOK - AAKASH SERIESCHAPTER - CALORIMETRY EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) (LECTURE SHEET (ADVANCED)(Matrix Type Questions)
1 Videos
Similar Questions
Knowledge Check
In a rectangle ABCD, AB= 15 cm ∠BAC=60∘ then BC is equal to
A15√3B15√32C15√3D152√3In a rectangle ABCD(BC=2AB). The moment of inertia is maximum along axis through
 ABCBABCHFDEG
ABCBABCHFDEGIn a rectangle ABCD(BC=2AB). The moment of inertia is minimum along axis through
 ABCBBDCHFDEG
ABCBBDCHFDEG
In rectangle ABCD, slope of AB=56. State the slope of
CD
View SolutionIn a rectangle ABCD (BC=2AB). The moment of inertia along which the axis will be minimum
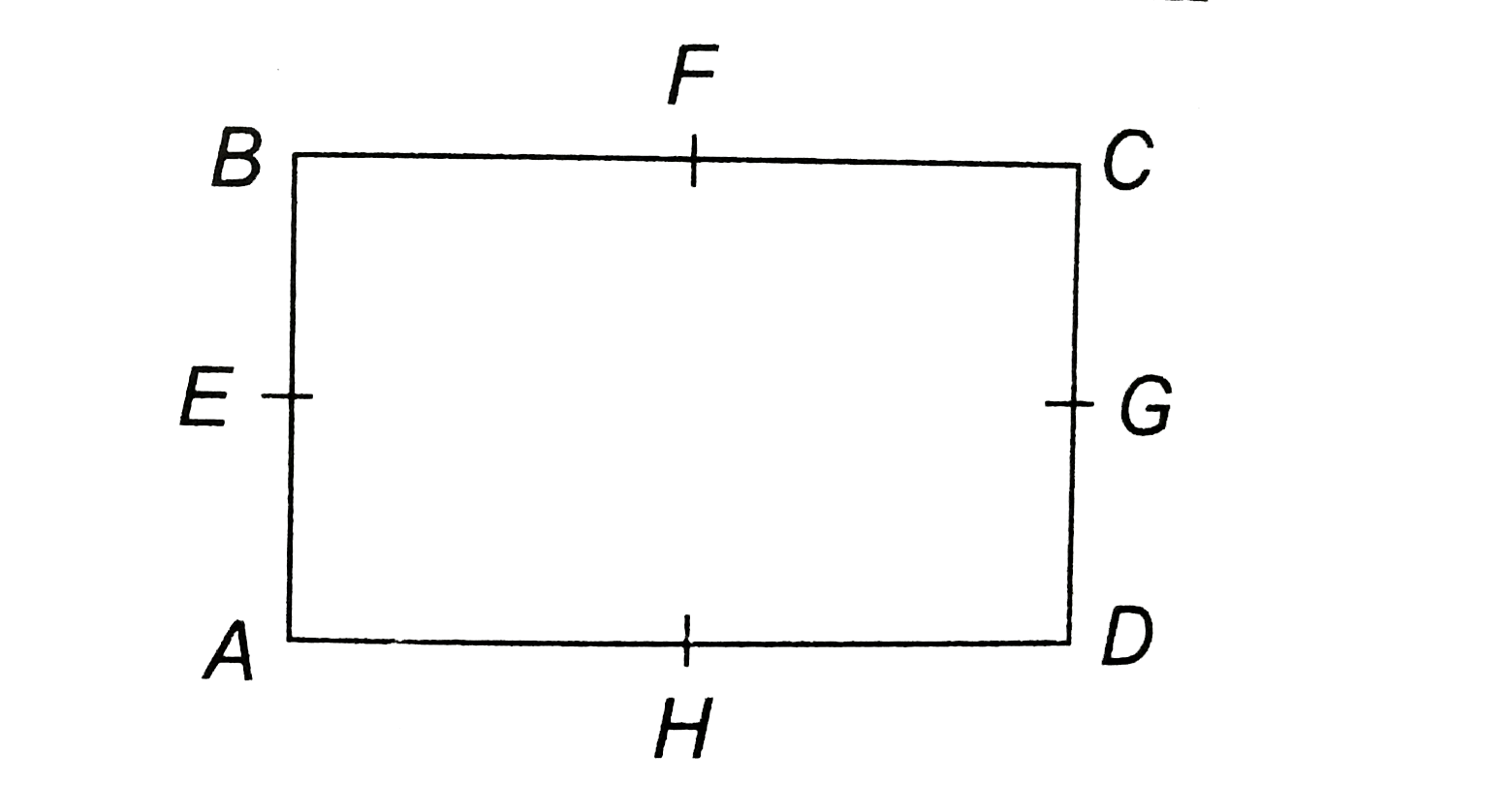
View SolutionIn a rectangle ABCD (BC=2AB). The moment of inertia along which axis will be minimum
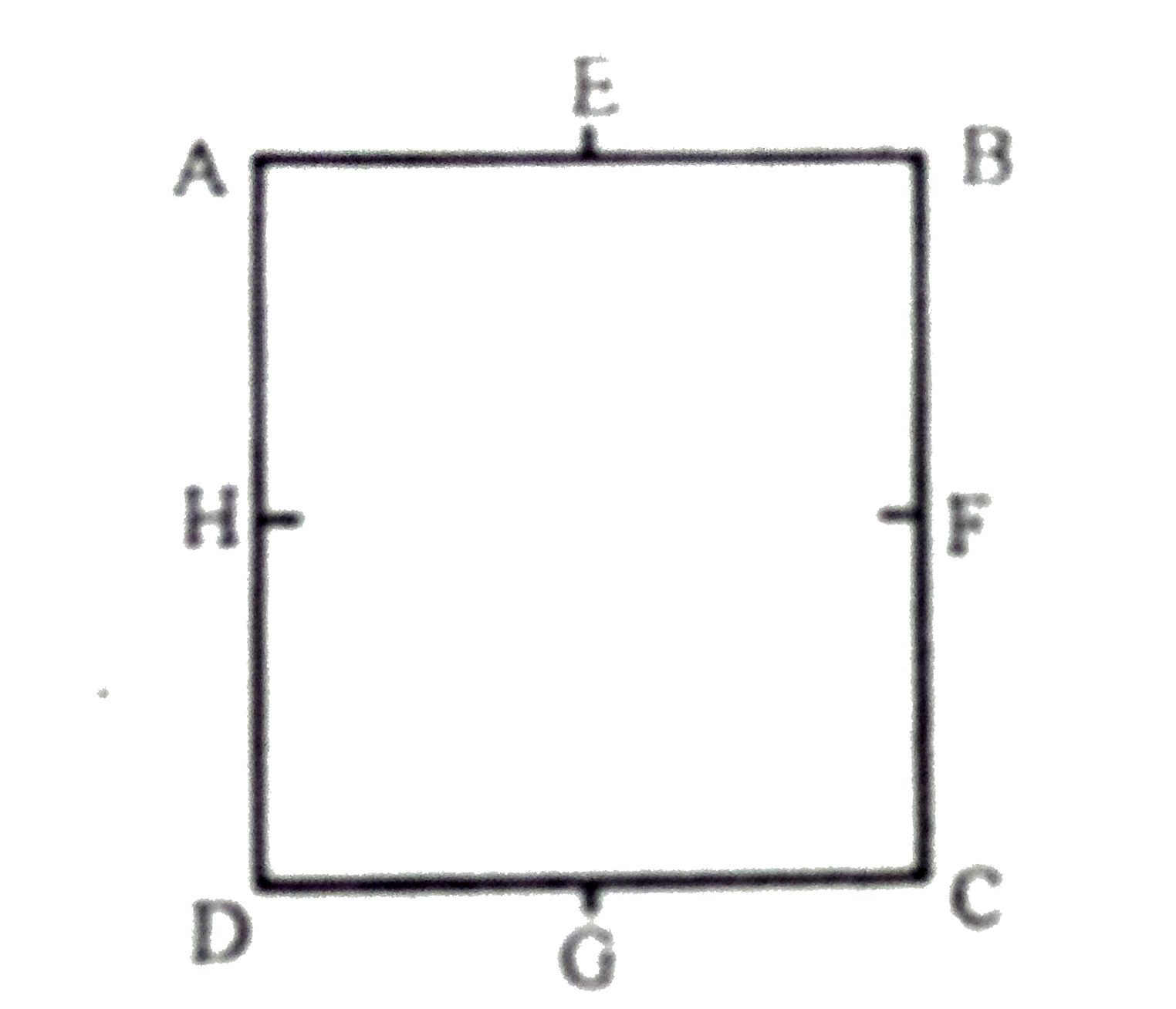
View SolutionIn a rectangle ABCD (BC=2AB). The moment of inertia along which the axis will be minimum

View SolutionIn a rectangle ABCD,AB=21 and BC=1. Axes × and yy pass through centre of the rectangle. The moment of inertia is least about :
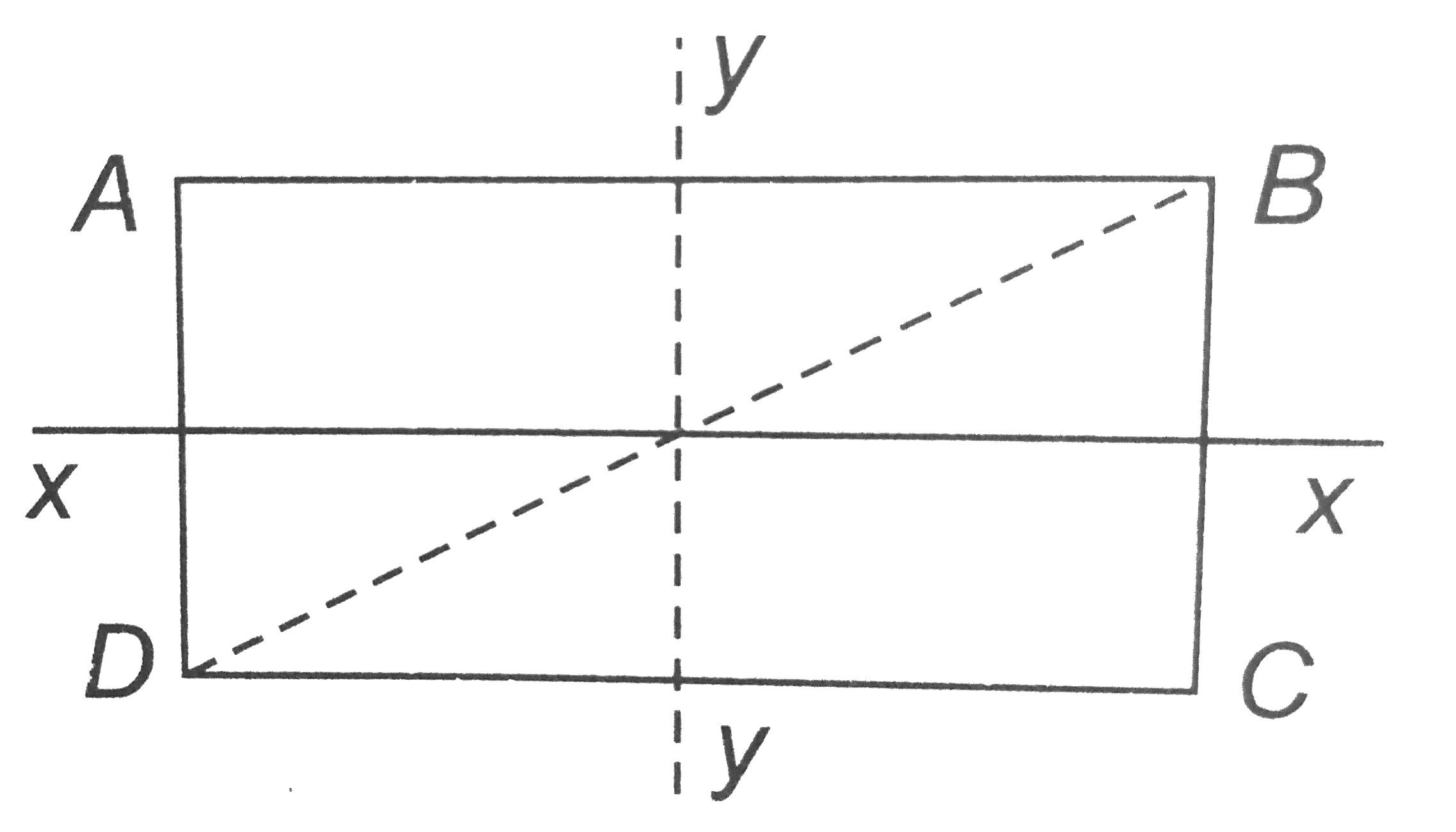 .
.
View Solution
