A wheel of radius 0.4 m can rotated freely about its axis as shown in the figure. A string is wrapped over its rim and a mass of 4 kg is hung, An angular acceleration of 8 rad is produced in it due to the torque. Then moment inergia of the wheel is (g = )
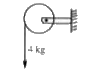
The correct Answer is:C
Topper's Solved these Questions
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - SYSTEM OF PARTICLES AND ROTATIONAL MOTION (ROLLING MOTION)
9 Videos
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - SYSTEM OF PARTICLES AND ROTATIONAL MOTION (EQUILIBRIUM OF BODY & PARALLEL FORCES)
6 Videos
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - SYSTEM OF PARTICLES AND ROTATIONAL MOTION (CONSERVATION OF ANGULAR MOMENTUM)
7 Videos
- CALORIMETRY BOOK - AAKASH SERIESCHAPTER - CALORIMETRY EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) (LECTURE SHEET (ADVANCED)(Matrix Type Questions)
1 Videos
Similar Questions
A wheel of radius 0.4m can rotate freely about its axis as shown in the figure. A string is wrapped over its rim and a mass of 4kg is hung. An angular acceleration of 8rad/s2 is produced in it due to the torque. Then, the moment of inertia of the wheel is (g=10m/s2)

View SolutionA wheel of radius 10 cm can rotate freely about its centre as shown in figure. A string is wrapped over its rim and is pulled by a force of 5.0 N. It is found that the torque produces an angular acceleration 2.0 rads−2 in the wheel. Calculate the moment of inertia of the wheel.

View Solution
Knowledge Check
A wheel of radius 0.4m can rotate freely about its axis as shown in the figure. A string is wrapped over its rim and a mass of 4kg is hung. An angular acceleration of 8rad/s2 is produced in it due to the torque. Then, the moment of inertia of the wheel is (g=10m/s2)
 A2kg−m2B1.36kg−m2C4kg−m2D8kg−m2
A2kg−m2B1.36kg−m2C4kg−m2D8kg−m2
A wheel of radius 10 cm can rotate freely about its centre as shown in figure. A stirng is wrapped over its rim and is ulle dby a force of 5.0 N. It is found that the torque roduces an angular acceleration 2.0 rads2 in the wheel. Calculate the moment of inertia of the wheel.

View SolutionA wheel of radius 20 cm and moment of inertia 1 kgm^2 can rotate about its centre.A string is wrapped over its rim and is pulled by a force 'F' tangential to the rim of wheel.If angular acceleration produced is 2 rad/s^2 then the value of force 'F' is
View SolutionA wheel of radius 20 cm and moment of inertia 1 kgm2 can rotate about its centre.A string is wrapped over its rim and is pulled by a force 'F' tangential to the rim of wheel.If angular acceleration produced is 2 rad/ s2 then the value of force 'F' is
View SolutionA wheel of mass 1.4 kg and radius 0.4 m is mounted on a frictionless, horizontal axle as shown in Fig. 7.2.50. Alight string wrapped around the rim supports a mass of 2 kg. What is the angular acceleration of the wheel and the tangential acceleration of a point on the rim ? Also find the tension in the string.
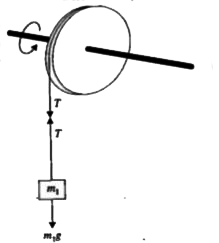
View SolutionA wheel of moment of inertia I and radius r is free to rotate about its centre as shown in figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. Find the speed of the block as it descends through a height h.
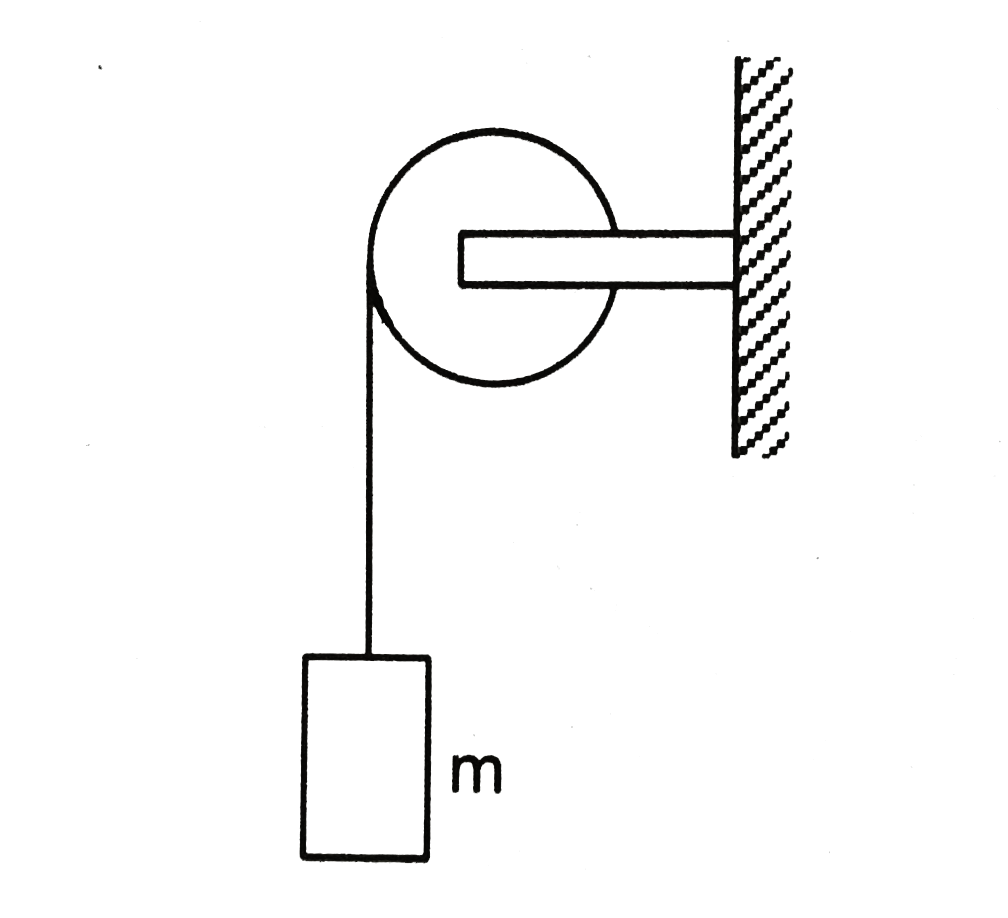
View SolutionCompute the torque acting on a wheel of moment of inertia 10kgm2, moving with angular acceleration 5rads−2.
View SolutionCompute the torque acting on a wheel of moment of inertia 10kgm2, moving with angular acceleration 5rads−2.
View Solution
