A wheel of radius 10 cm can rotate freely about its centre as shown in figure. A stirng is wrapped over its rim and is ulle dby a force of 5.0 N. It is found that the torque roduces an angular acceleration 2.0 rads2 in the wheel. Calculate the moment of inertia of the wheel.

The forces acting on the wheel are i. W due to gravity ii N due to the support at the cnetre and iii F due to tension. The torque of W and N are separately zero and that of F is F.r. The net torque is
Γ=(5.0N).(10cm)=0.50N.m.
The moment of inertia is
I=Γa=0.50N−m2rads62=0.25kg−m2
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:HC VERMAChapter:ROTATIONAL MECHANICSExercise:Worked Out Examples
Explore 29 Videos
- ROTATIONAL MECHANICSBook:HC VERMAChapter:ROTATIONAL MECHANICSExercise:Short Answer
Explore 22 Videos
- REST AND MOTION : KINEMATICSBook:HC VERMAChapter:REST AND MOTION : KINEMATICSExercise:Exercises
Explore 51 Videos
- SIMPLE HARMONIC MOTIONBook:HC VERMAChapter:SIMPLE HARMONIC MOTIONExercise:Exercises
Explore 58 Videos
Similar Questions
A wheel of radius 20 cm and moment of inertia 1 kgm2 can rotate about its centre.A string is wrapped over its rim and is pulled by a force 'F' tangential to the rim of wheel.If angular acceleration produced is 2 rad/ s2 then the value of force 'F' is
View SolutionIf a 42.0N⋅m torque on a wheel causes angular acceleration 25.0rad/s2, what is the wheel's rotational inertia?
View Solution
Knowledge Check
A wheel of radius 0.4m can rotate freely about its axis as shown in the figure. A string is wrapped over its rim and a mass of 4kg is hung. An angular acceleration of 8rad/s2 is produced in it due to the torque. Then, the moment of inertia of the wheel is (g=10m/s2)
 A2kg−m2B1.36kg−m2C4kg−m2D8kg−m2
A2kg−m2B1.36kg−m2C4kg−m2D8kg−m2A constant torque of 3.14 N mis exerted on a pivoted wheel. If the angular acceleration of the wheel is 4πrad/s2 then the moment of inertia of the wheel is
A0.25kgm2B2.5kgm2C4.5kgm2D25kgm2A constant torque of 31.4N−m is exterted on a pivoted wheel. If the angular acceleration of the wheel is 4πrad/s2, then the moment of inertia will be.
A2.5kg−m2B5.8kg−m2C4.5kg−m2D5.6kg−m2
A wheel of moment of inertia I and rdius r is free to rotate about its centre as shown in figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. Find the speed of the block as it descends through a height h.
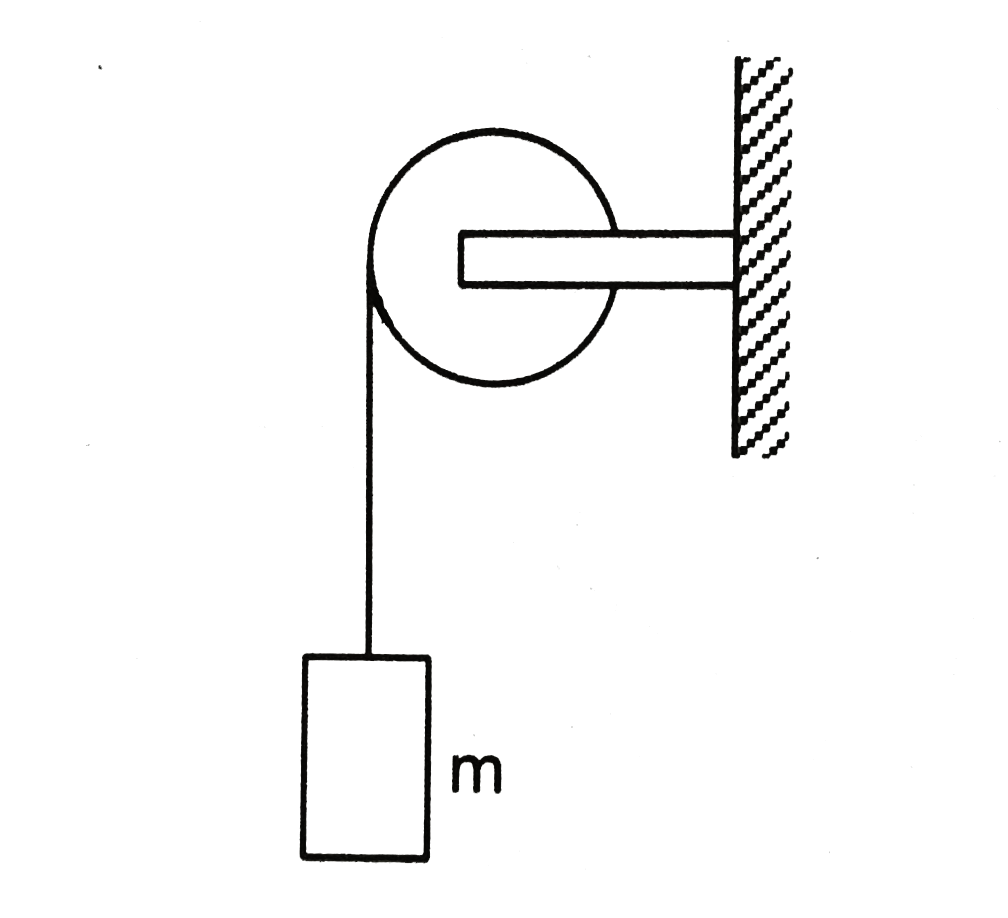
View SolutionA cord is wound around the circumference of a wheel of diameter 0.3 m. The axis of the wheel is horizontal. A mass of 0.5 kg is attached at the end of the cord and it is allowed to fall from rest. If the weight falls 1.5 m in 4s, what is the angular acceleration of the wheel ? Also find out the moment of inertia of the wheel.
View SolutionCompute the angular acceleration of a wheel having moment of inertia 20kgm2, when a torque of 10Nm is applied on the wheel.
View SolutionA wheel of radius 15cm is rotating about its axis at angluar speed of 20rad/s. Find the linear speed and total acceleration of a point on the rim.
View SolutionA constant torque of 31.4 Nm is applied to a pivoted wheel. If the angular acceleration of the wheel is 2π rad/s2, then its moment of inertia is
View Solution