A heated object (at time t = 0 and temperature $T = T_{0}$ ) is taken out of the oven to cool and placed on a table near an open window. Write an depression for its temperature as a function of time T, where $T_{S}$ is the surrounding temperature

A

$T = T_{S} - (T_{0} - T_{S}) e^{- k t}$

B

$T = T_{S} + (T_{0} + T_{S}) e^{- k t}$

C

$T = T_{S} + (T_{0} - T_{S}) e^{- k t}$

D

$T - T_{S} - (T_{0} - T_{S}) e^{- k t}$

Text Solution

Verified by Experts

The correct Answer is:C

|

Updated on:21/07/2023

Class 11 PHYSICS THERMAL EXPANSION AND CALORIMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A heated object (at time $t = 0$ and temperature $T = T_{0})$ is taken out of the oven to cool and placed on a table near an open window Write an expression for its temperature as function of time $T$ where $T_{s}$ is the surrounding temperature .
A $T = T_{s} - (T_{0} + T_{s}) e^{- k t}$
B $T = T_{s} + (T_{0} + T_{s}) e^{- k t}$
C $T = T_{s} + (T_{0} - T_{s}) e^{- k t}$
D $T = T_{s} - (T_{0} - T_{s}) e^{- k t}$
Question 2 - Select One
If a piece of metal is heated to temperature $θ$ and the allowed to cool in a room which is at temperature $θ_{0}$ , the graph between the temperature T of the metal and time t will be closet to
A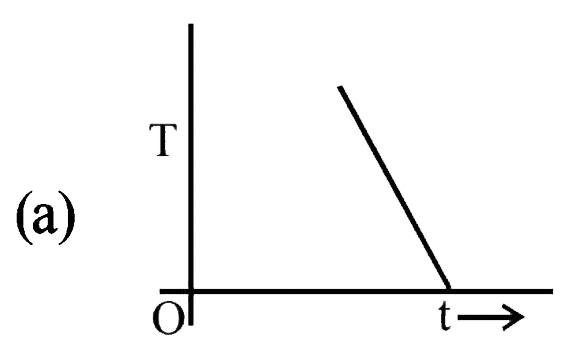
B
C
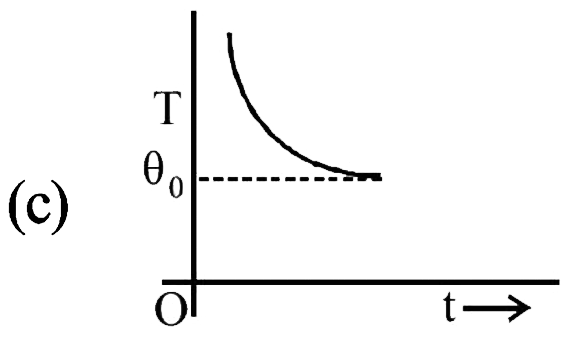D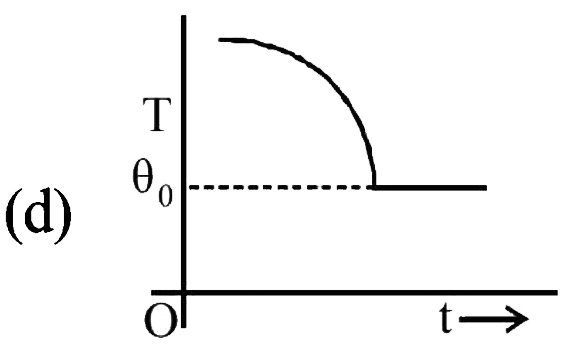
Question 3 - Select One
A body at temperature $θ_{0}$ having Newton's cooling constant K is placed in a surrounding having temperature $T_{0}$ at time t = 0. The graph of temperature of the body as a function of time t is shown in the adjacent figure. A tangent on the curve is drawn at t = 0 as shown in the figure. Find the value of $τ$ .

AK
B $\frac{1}{K}$
C $K (Q_{0} - T_{0})$
DData insufficient

AAKASH SERIES-TRANSMISSION OF HEAT-ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED)) (Integer/Subjective Type Questions)

Home
Ask Doubt
Profile