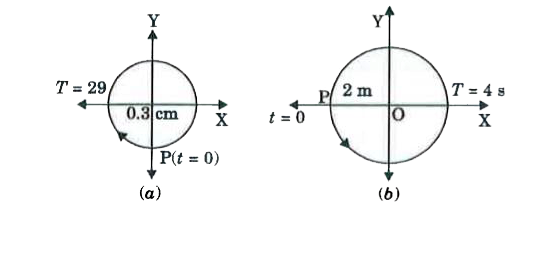
Figures 14.25 correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e. clockwise or anti-clockwise) are indicated on each figure.
Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P, in each case.
(a) x = - 3 sin πt where x is in cm.
(b) x = - 2 cos π2t where x is in cm.
Topper's Solved these Questions
- OSCILLATIONSBOOK - NCERT TELUGUCHAPTER - OSCILLATIONSEXERCISE - Additional Exercises
6 Videos
- OSCILLATIONSBOOK - NCERT TELUGUCHAPTER - OSCILLATIONSEXERCISE - Additional Exercises
6 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT TELUGUCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ADDITIONAL EXERCISES
5 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - NCERT TELUGUCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISES (TRUE OR FALSE)
5 Videos
Similar Questions
Figure below correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e. clockwise or anticlockwise) are indicated on each figure. Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P in each case.
View SolutionFigures,. Correspond to two circular motions. The radius of the circle, the peirod of revolution, the initial position, and the sense of revolution (i.e. clockwise or anticlockwise) are indicated on each. Obtain the corresponding equations of simple harmonic motions of the revolving particle P in each case.
View Solution
Knowledge Check
The following figure depicts two circular motions. The radius of the circle, the period of revolutin the initial position and the sense of revolution are indicated on the figure. Obtain the simple harmoic motion of the x-projection of the radius vector of the rotating particle P in each case.
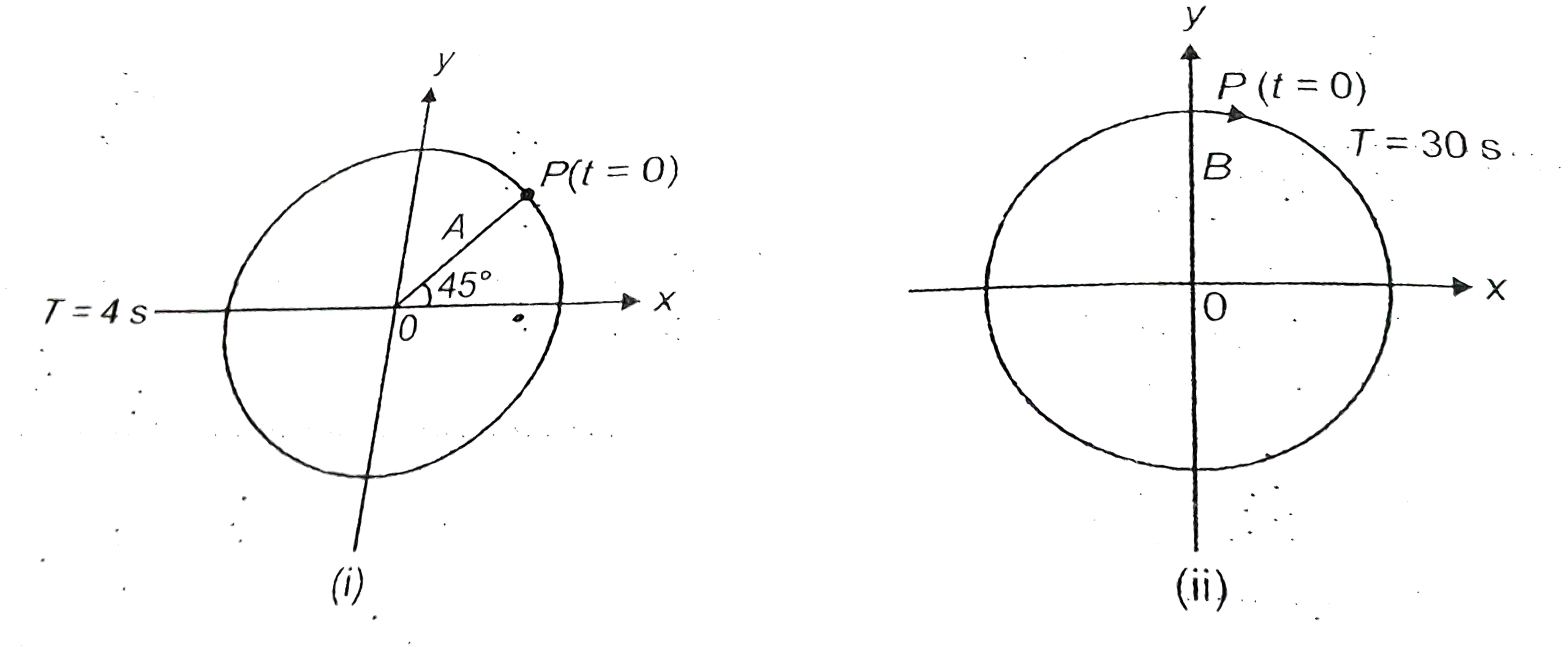Ax(t)=acos(2πt4+π4)Bx(t)=acos(πt4+π4)Cx(t)=asin(2πt4+π4)Dx(t)=acos(πt3+π2)the circular motion of a particle. The radius of the circle, the period, sense of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector of the rotating particle P is
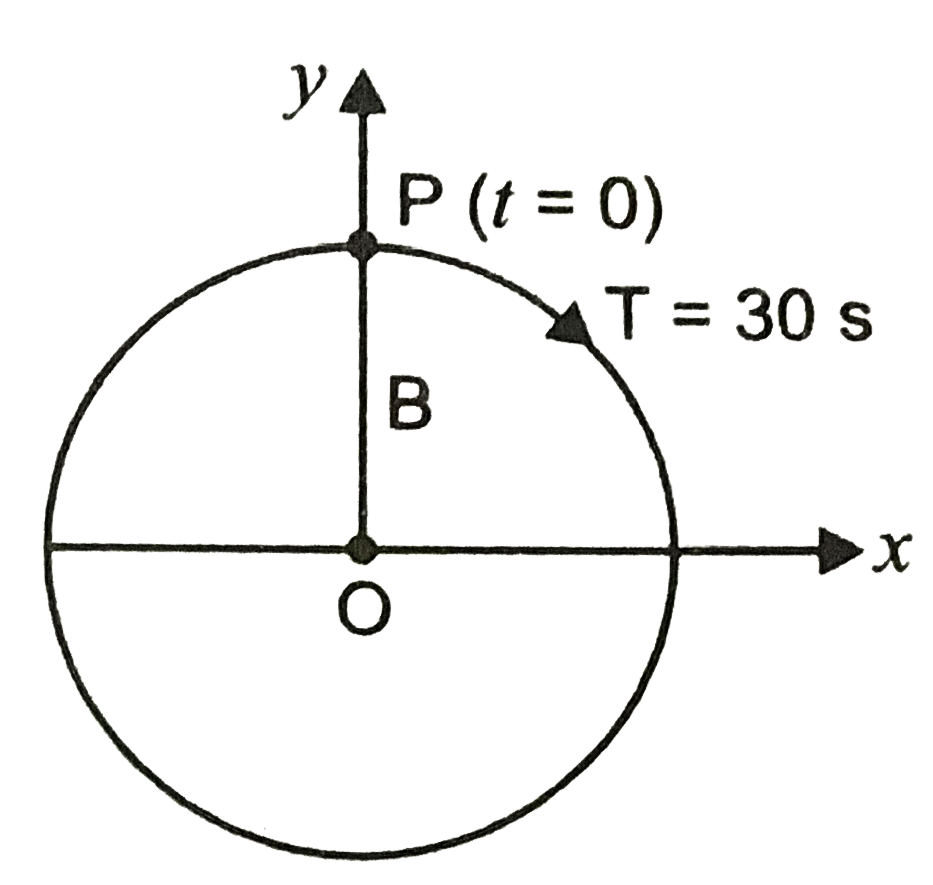Ax(t)=Bsin(2πt30)Bx(t)=Bcos(πt15)Cx(t)=Bsin(πt15+π2)Dx(t)=Bcos(πt15+π2)
From the figure, obtain the equation of simple harmonic motion of the y-projection of the radius vector of the revolving particle P in each case.
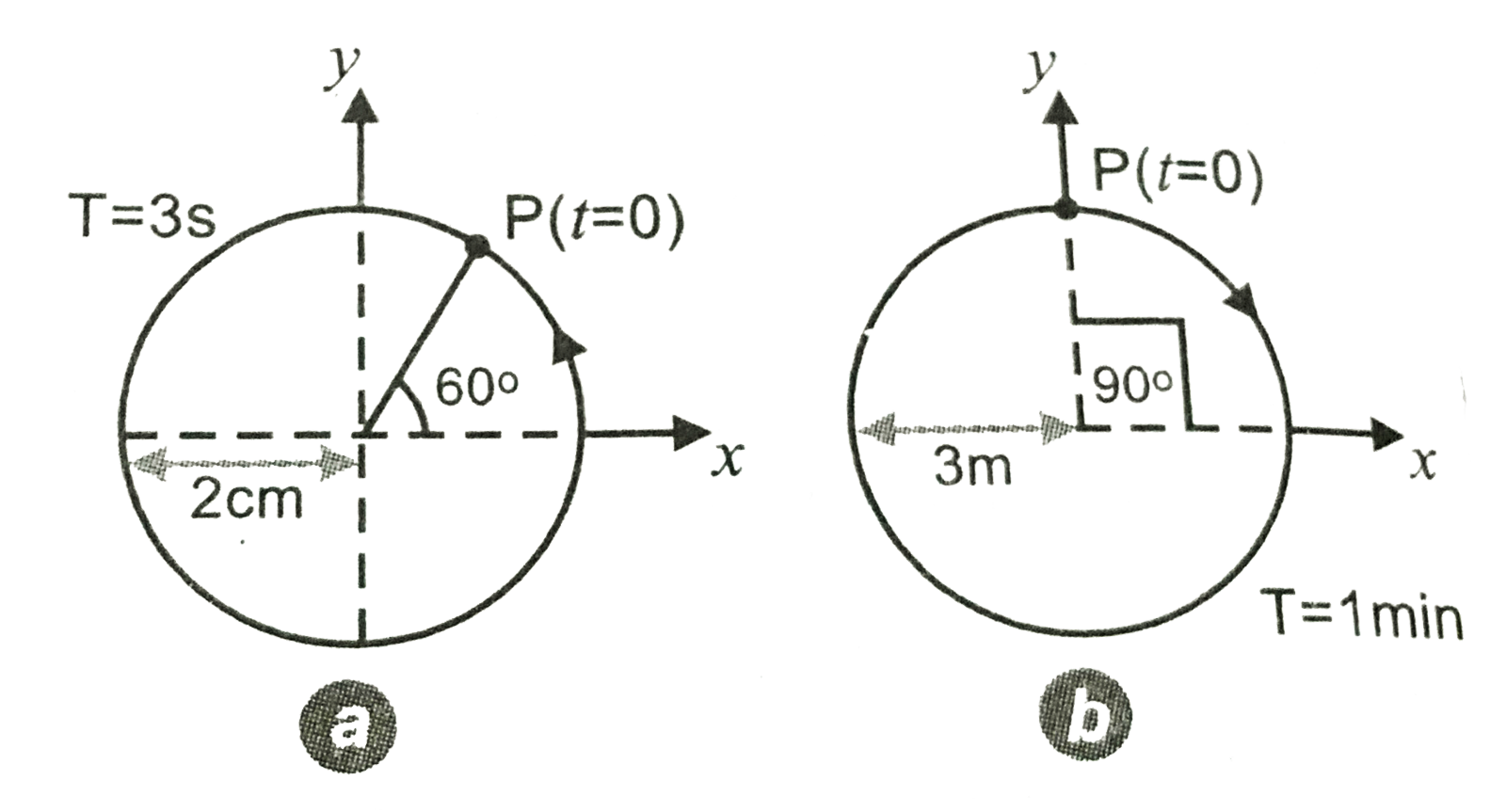
View SolutionThe following figure depicts two circular motions. The radius of the circle, the period of revolutin the initial position and the sense of revolution are indicated on the figure. Obtain the simple harmoic motion of the x-projection of the radius vector of the rotating particle P in each case.
View SolutionThe following figure depicts two circular motions. The radius of the circle, the period of revolutin the initial position and the sense of revolution are indicated on the figure. Obtain the simple harmoic motion of the x-projection of the radius vector of the rotating particle P in each case.
View Solutiondepict two circulat mothions. The radius of the circle, the period of revolution, the initial position and sense of revolution are indicated in the figures. Obtain the simple harmonic motinosof the x-projection of the radius vector of the rotating particle P in each case.
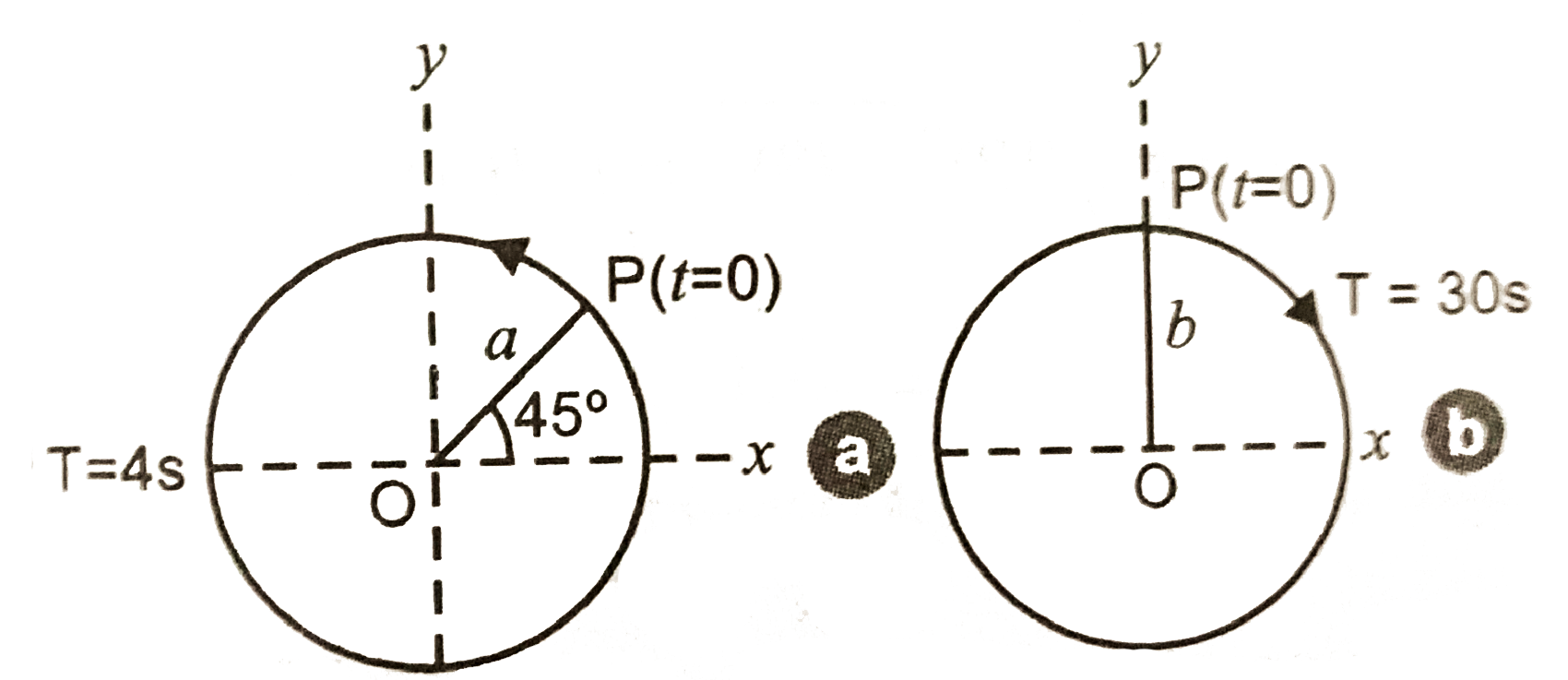
View Solution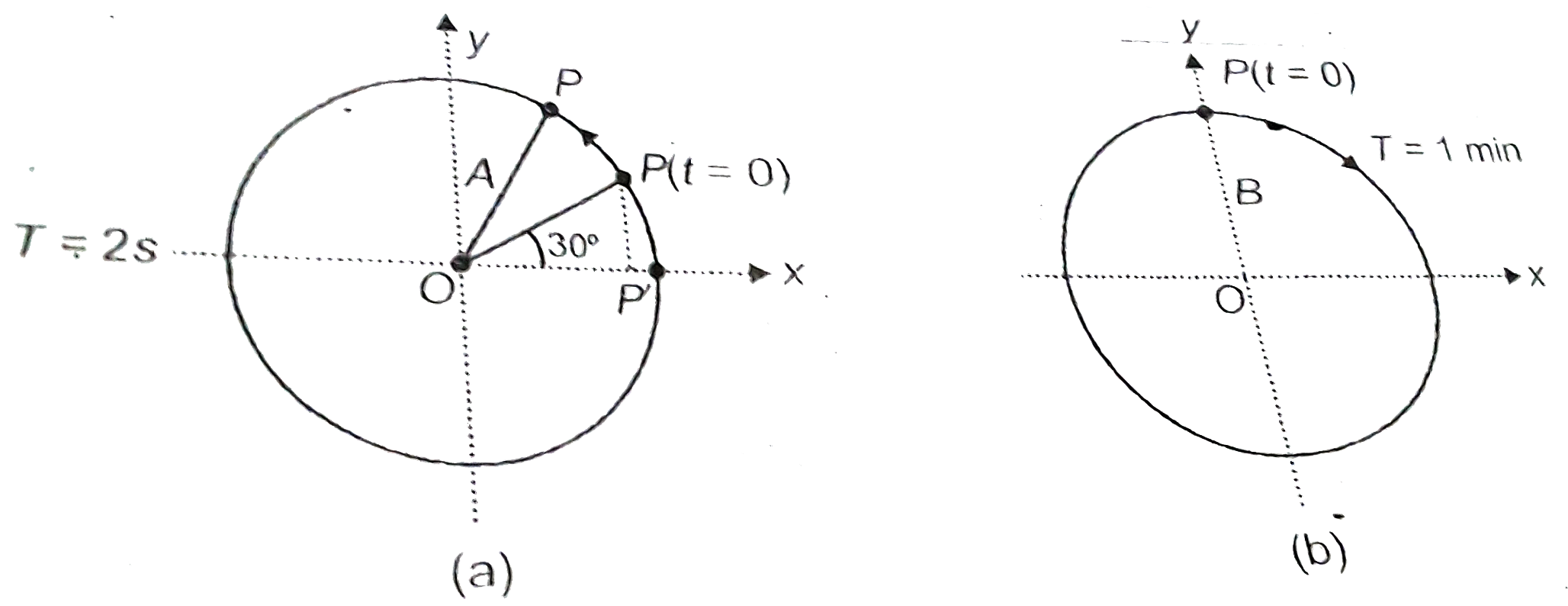
Figure depicts two circular motions. The radius of the circle, the period of revolution, the initial position and the sense of revolution are indicated on the figure. Obtain the SHMs of the x-projection of the radius vector of the rotating particle P in each case.
View Solution-
Figure depicts two circular motions. The radius of the circle, the period of revolution, the initial position and the sense of revolution are indicated on the figure. Obtain the SHMs of the x-projection of the radius vector of the rotating particle P in each case.
View Solution