A mass m is released from the top of a vertical circular track of radius r with a horizontal speed v0. Calculate the angle θ with respect o the vertical where it leaves contact with the track. Solution in Telugu
The forces acting on the body are its weight mg and reaction N as shown in Fig.
So for circular motion of the body at any position θ
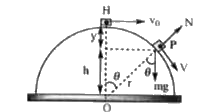 mv2r=mgcosθ−NorN=mgcosθ−mv2r
mv2r=mgcosθ−NorN=mgcosθ−mv2r
The body will have contact where N = 0
i.e., mg cosθ=mv2r=0
i.e, cosθ=v2rg .............(2)
Now applying conservation of mechanical energy between H and P, we get
12mv2=12mv20+mgr(1−cosθ)
where .v. is the velocity at .P. [asy=r(1−cosθ)]
orv2=v20+2gr(1−cosθ).........(3)
substituting the value of v2 in Equation (2)
cosθ=v20rg+2(1−cosθ)
i.e.,cosθ=[v203rg+23]orθ=cos−1[v203rg+23]
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - WORK, POWER & ENERGY EXERCISE - EXERCISE - I78videos
WORK, POWER & ENERGY
- BOOK - AAKASH SERIESCHAPTER - WORK, POWER & ENERGY EXERCISE - EXERCISE - II (SCALARS (OR) DOT PRODUCT)9videos
WORK, POWER & ENERGY
- BOOK - AAKASH SERIESCHAPTER - WORK POWER ENERGYEXERCISE - EXERCISE - 361videos
WORK POWER ENERGY
Similar Questions
If l1,m1,n1 and l2,m2,n2 are the direction cosines of two vectors and θ is the angle between them, then the value of cos θ is
03:19View SolutionIf →P=2ˆi+3ˆj−4ˆkand→Q=5ˆi+2ˆj+4ˆk. Find the angle between the two vectors.
02:45View SolutionIf →A+→B=→Rand2→A+→B is perpendicular to →B then
04:06View SolutionA section of fixed smooth circular track of radius R in vertical plane is shown in the figure. A block id released from position A and leaves the treack at B The radius of curvanture of its trajectory just after it leaves the track B is ?
01:48View SolutionA particle of mass m is released from the top of a smooth hemisphere of radius R with the horizontal speed μ. Calculate the angle with verticle where it loses contact with the hemisphere.
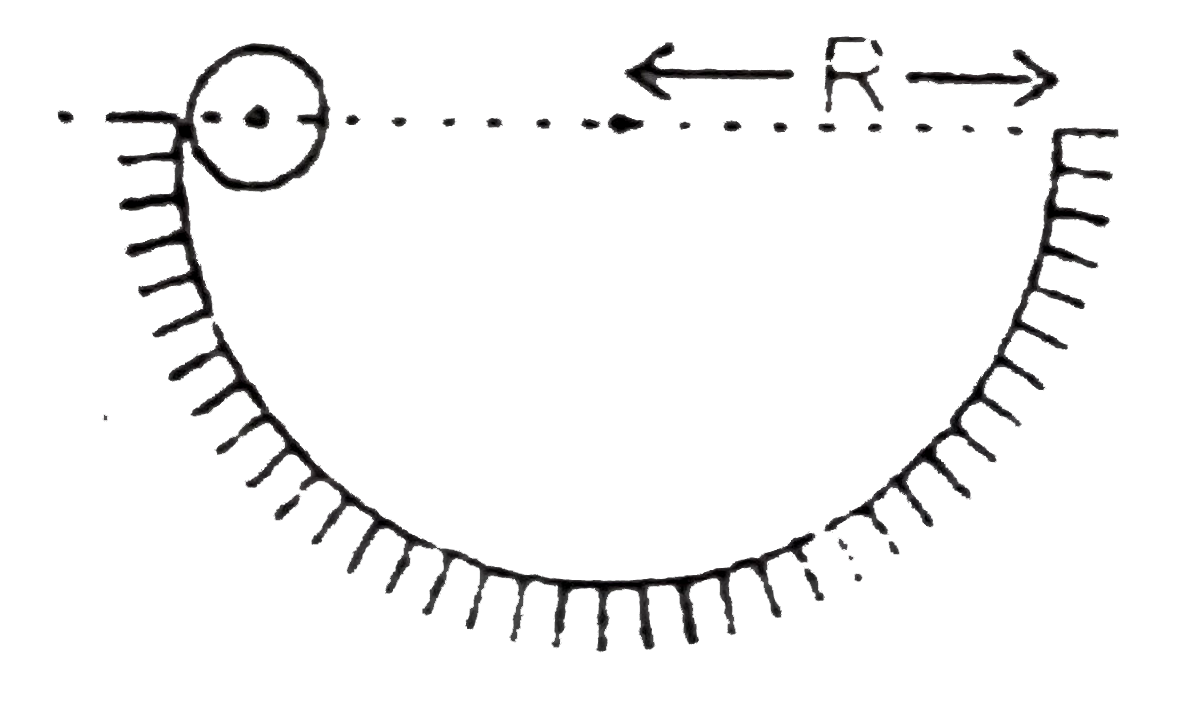
05:28View SolutionIn the figure shown, a small ball of mass 'm' can move witgout sliding in a fixed semicircular track of radius R in vertical planet. It is released from the top. The resultant force on the ball at the lowest of the track is
 03:28View Solution
03:28View SolutionIn a circus stuntman rides a motorbike in a circular track of radius R in the vertical plane. The minimum speed at highest point of track will be
01:56View SolutionAs shown in the figure, a small is released from a certain height h which has to perform circular motion on a vertical smooth track of radius 4 m. the track is absent between point A and B. Calculate the height (in m) from where the ball has to be released so that it will reach at highest point B of the circular track
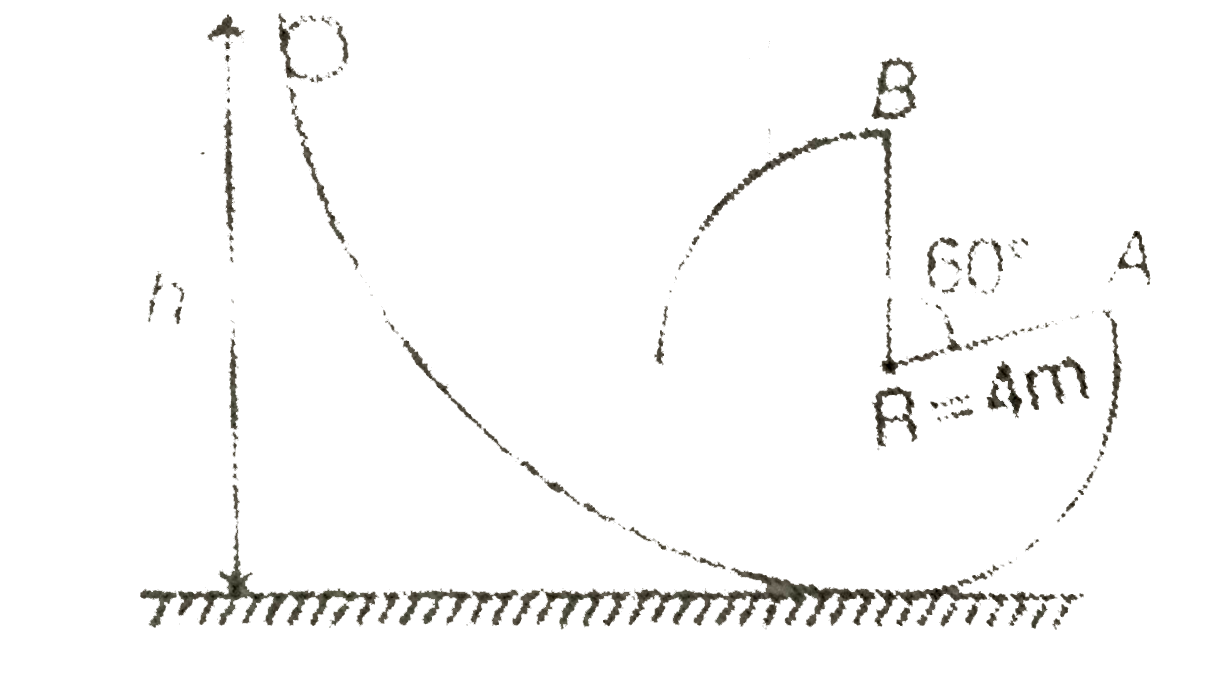 View Solution
View SolutionIn a circus , stuntman rides a motor bike in a circular track of radius R in the vertical plane. The minimum speed at highest point of track will be _______ .
05:21View SolutionAn inclined track ends in a circular loop of radius 'r'. From what height on the track a particle should be released so that it completes that loop in the vertical plane?
View SolutionA mass m is released with a horizontal speed v from the top of a smooth and fixed, hemispherical bowl, of radius r. The angle theta w.r.t the vertical where it leaves contact with the bowl is
View SolutionA mass m is released from the top of a vertical circular track of radius r with a horizontal speed v0. Calculate the angle θ with respect o the vertical where it leaves contact with the track.
View SolutionA mass .m. is released, with a horizontal speed v from the top of a smooth and fixed, hemispherical bowl, of radius r. The angle theta w.r.t. the vertical where it leaves constant with the bowl is
View SolutionA mass.m. is released, with a horizontal speed v from the top of a smooth and fixed, hemispherical bowl, of radius r. The angle theta w.r.t. the vertical where it leaves contact with the bowl is
View SolutionA mass 'm' is released, with a horizontal speed v from the top of a smooth and fixed, hemispherical bowl, of radius r. the angle θ w.r.t. the vertical where it leaves contact with the bowl is
03:57View Solution

