Prove that in case of oblique elastic collision of two particles of equal mass if one is at rest, the recoiling particles always move off at right angles to each other.

Text Solution

Verified by Experts

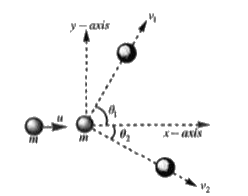
In elactic collision momentum is conserved.
So, conservation of momentum along x - axis yields.
$μ = m v_{1} {cos θ}_{1} + m v_{2} {cos θ}_{2}$
$i . e ., u = v_{1} {cos θ}_{1} + v_{2} {cos θ}_{2} ... . (1)$
and along y - axis yields
$0 = v_{1} {sin θ}_{1} - v_{2} {sin θ}_{2} ... . (2)$
Squaring and adding Eqns. (1) and (2), we get
$u^{2} = v_{1}^{2} + v_{2}^{2} + 2 v_{1} v_{2} cos (θ_{1} + θ_{2}) ... . (3)$
As the collision is elactic $\frac{1}{2} m u^{2} = \frac{1}{2} m v_{1}^{2} + \frac{1}{2} m v_{2}^{2}$
$i . e ., u^{2} = v_{1}^{2} + v_{2}^{2} ... . (4) Put u^{2} = v_{1}^{2} + v_{2}^{2}$ in Eqn (3).
we get $2 v_{1} v_{2} cos (θ_{1} + θ_{2}) = 0$
As it is given that $v_{1} \neq 0 and v_{2} \neq 0$
so $cos (θ_{1} + θ_{2}) = 0, i . e ., (θ_{1} + θ_{2}) = 90^{\circ}$

Updated on:21/07/2023

A ball of mass m moving with a velocity v undergoes an oblique elastic collision with another ball of the same mass m but at rest. After the collision if the two balls move with the same speeds , the angle between their directions of motion will be:
A $30^{\circ}$
B $60^{\circ}$
C $120^{\circ}$
D $90^{\circ}$
A particle of mass m moving with velocity $\to V$ makes a head on elastic collision with another particle of same mass initially at rest. The velocity of the first particle after the collision will be
A $\to V$
B $- \to V$
C $- 2 \to V$
DZero
A particle of mass m moving with velocity $\to V$ makes a head on elastic collision with another particle of same mass initially at rest. The velocity of the first particle after the collision will be
A $\to V$
B $- \to V$
C $- 2 \to V$
Dzero