Three equal masses of m kg each are fixed at the vertices of an equilateral triangle ABC
a) What is the force acting on a mass 2m placed at the centroid G of the triangle.
b) What is the force if the mass at the vertex A is doubled? Take AG = BH = 1m
The individual forces in vector notation are
FGA=G(m)(2m)1ˆj
FGB=G(m)(2m)1(−ˆicos30∘−ˆjsin30∘)
FGC=G(m)(2m)1(ˆicos30∘−ˆjsin30∘)
From the principle of superposition and law of vector addition the resultant gravitational force FR on (2m) is
FR=FGA+FGC
FR=2Gm2ˆj+2Gm2(−ˆicos30∘−ˆjsin30∘)
+2GM2(ˆicos30∘−ˆjsin30∘)=0
b) By symmetry , the X - component of the force cancels out . The Y - component survies .
∴FR=4Gm2ˆj−2Gm2ˆj=2Gm2ˆj
Topper's Solved these Questions
- GRAVITATIONBOOK - AAKASH SERIESCHAPTER - GRAVITATIONEXERCISE - Exercise-I
124 Videos
- GRAVITATIONBOOK - AAKASH SERIESCHAPTER - GRAVITATIONEXERCISE - Exercise-II
78 Videos
- GAUSS.S LAW BOOK - AAKASH SERIESCHAPTER - GAUSS.S LAW EXERCISE - PROBLEMS (LEVEL - II)
12 Videos
- GRAVITATIONALBOOK - AAKASH SERIESCHAPTER - GRAVITATIONALEXERCISE - EXERCISE -3
154 Videos
Similar Questions
Three equal masses of mkg each are fixed at the vertices of an equilateral triangle ABC.
a. What is the force acting on a mass 2m placed at the centroid G of the triangle?
b. What is the force if the mass at the vertex A is doubled? Take AG=BG=CG=1m
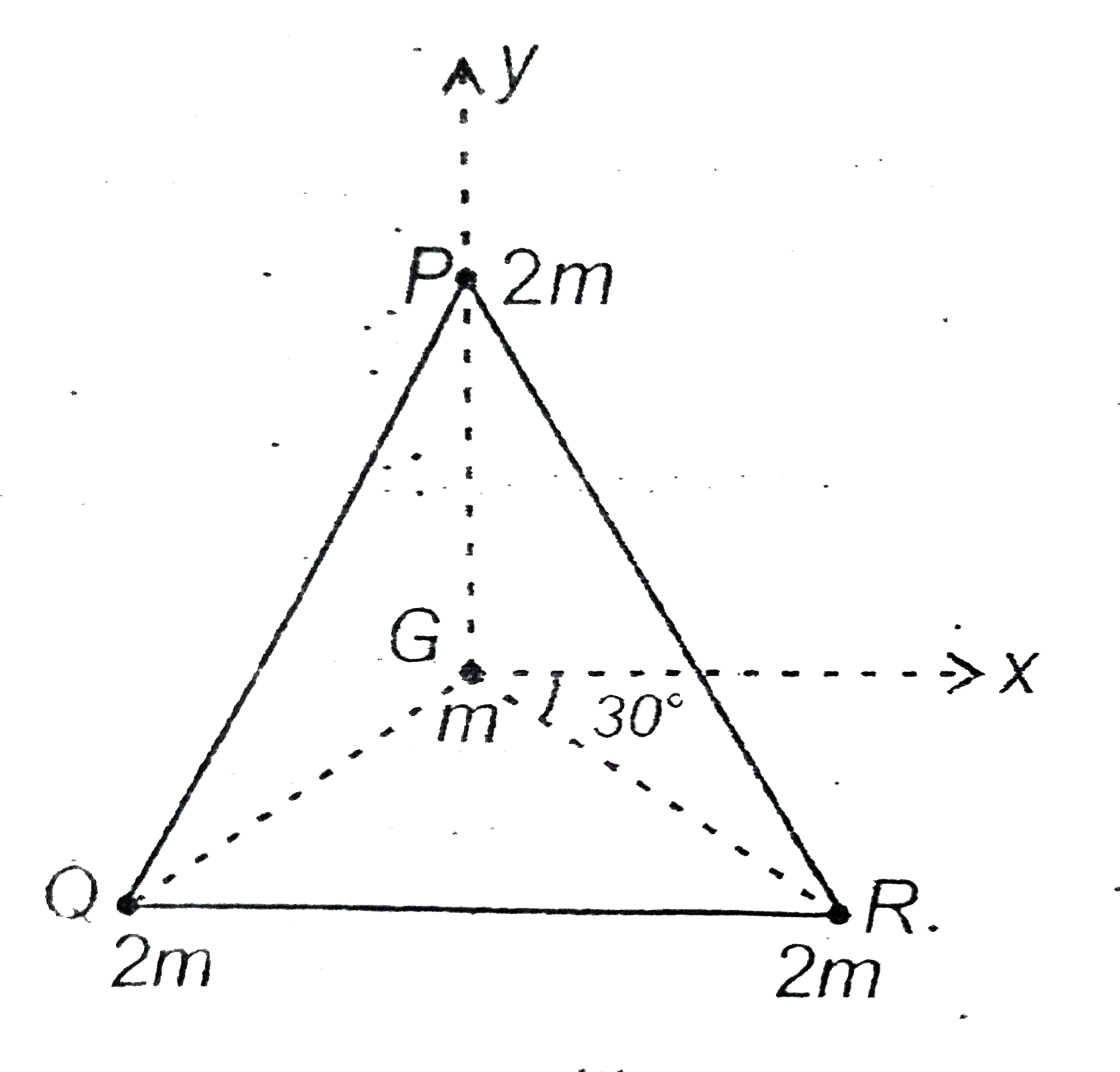
View SolutionThree equal masses 2m each are placed at the vertices an equilateral triangle PQR
(i) What is the force acting on a mass m placed at the centroid G of the triangle ?
(ii) What is the force on mass m if the mass at the vertex P is quadrupled ?
Take PG = QG = RG = 1m
View Solution
Knowledge Check
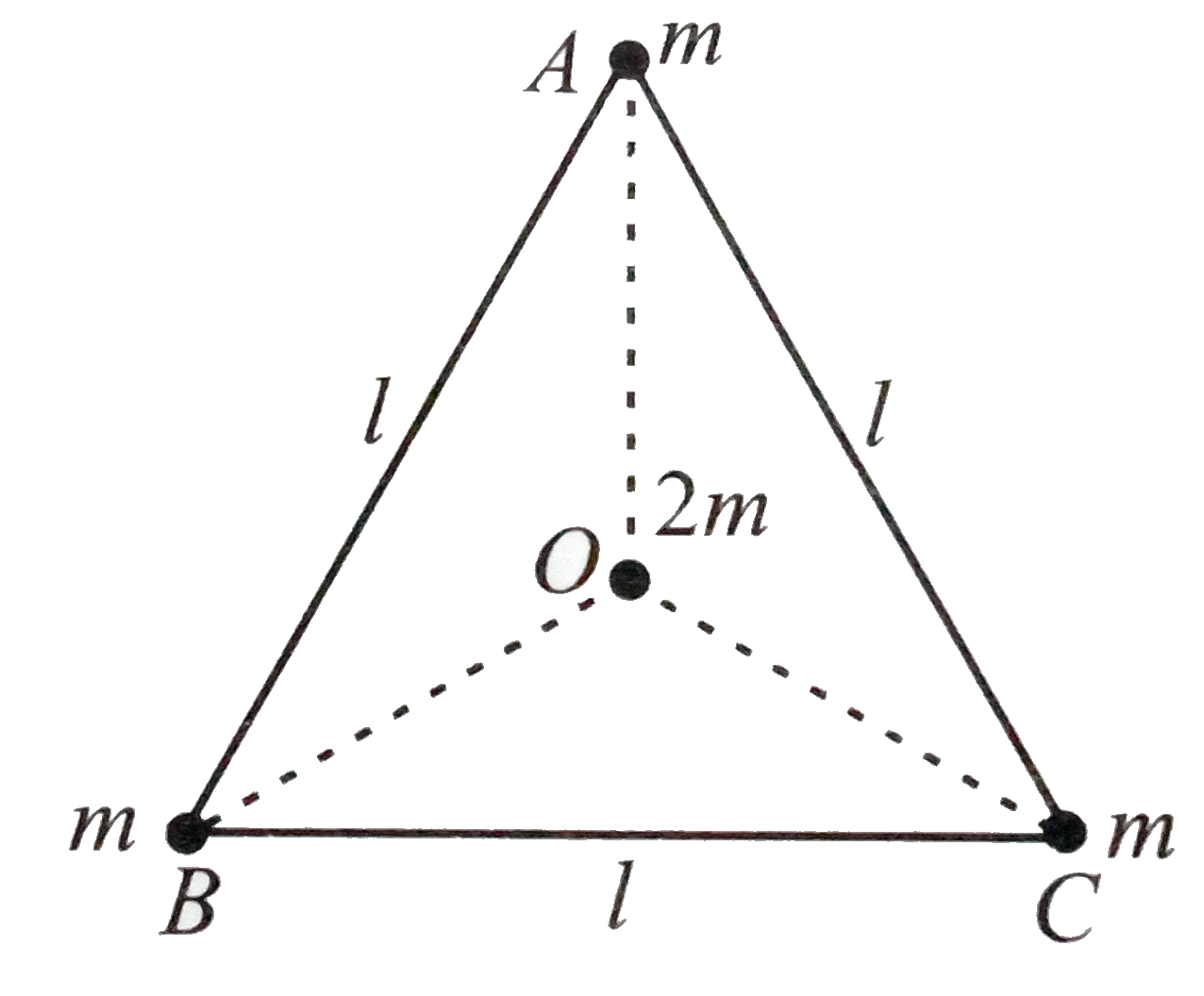
Three masses each of mass m are placed at the vertices of an equilateral triangles ABC of side l as shown in figure. The force acting on a mass 2m placed at the centroid O of the triangle is
 AzeroB3Gm2l2C5Gm2l2D7Gm2l2
AzeroB3Gm2l2C5Gm2l2D7Gm2l2Three masses each of mass m are palced at the vertices of an equilateral triangles ABC of side l as shown in figure. The force acting on a mass 2m placed at the centroid O of the triangle is
 AzeroB3Gm2l2C5Gm2l2D7Gm2l2
AzeroB3Gm2l2C5Gm2l2D7Gm2l2Three particles each of mass m are kept at the vertices of an euilateral triangle of side L. The gravitational field at the centre due to these particle is
A−3GMLB−√3GMLC−3√3GMLD−GM3√3L
Three equal masses 2m each are placed at the vertices an equilateral triangle PQR
(i) What is the force acting on a mass m placed at the centroid G of the triangle ?
(ii) What is the force on mass m if the mass at the vertex P is quadrupled ?
Take PG = QG = RG = 1m

View SolutionThree equal masses of 1.5 kg each are fixed at the vertices of an equilateral triangle of side 1 m. What is the force acting on a particle of mass 1 kg placed at its centroid ?
View SolutionThree equal masses of 1.5 kg each are fixed at the vertices of an equilateral triangle of side 1 m. What is the force acting on a particle of mass 1 kg placed at its centroid ?
View SolutionThree masses of 1 kg each are kept at the vertices of an equilateral triangle of side 3 m. What is the force acting on a point mass of 5 kg placed at its centroid ?
View SolutionThree masses of 1 kg each are kept at the vertices of an equilateral triangle of side 3 m. What is the force acting on a point mass of 5 kg placed at its centroid ?
View Solution
