Three masses of 1 kg each are kept at the vertices of an equilateral triangle of side 3 m. What is the force acting on a point mass of 5 kg placed at its centroid ?
The correct Answer is:Zero
To solve the problem of finding the net gravitational force acting on a point mass of 5 kg placed at the centroid of an equilateral triangle with three 1 kg masses at its vertices, we can follow these steps:
Step 1: Understand the Setup
We have three masses (m1, m2, m3) of 1 kg each located at the vertices of an equilateral triangle with a side length of 3 m. The point mass (M) of 5 kg is placed at the centroid of the triangle.
Step 2: Calculate the Distance from the Centroid to the Vertices
For an equilateral triangle, the distance (r) from the centroid to any vertex can be calculated using the formula:
r=a√3
where a is the side length of the triangle. Here, a=3m.
r=3√3=√3m≈1.732m
Step 3: Calculate the Gravitational Force Exerted by Each Mass
The gravitational force F exerted by each mass on the point mass can be calculated using Newton's law of gravitation:
F=G⋅m⋅Mr2
where:
- G is the gravitational constant 6.674×10−11N m2/kg2
- m=1kg (mass at the vertex)
- M=5kg (mass at the centroid)
- r=√3m
Substituting the values:
F=6.674×10−11⋅1⋅5(√3)2
F=6.674×10−11⋅53
F=33.37×10−113≈11.12×10−11N
Step 4: Analyze the Forces Acting on the Point Mass
Each of the three forces F1,F2,F3 acts along the lines connecting the centroid to each vertex. Since the triangle is equilateral, the angle between any two forces is 120∘.
Step 5: Calculate the Resultant Force
To find the resultant force FR acting on the point mass, we can use the vector addition of the forces. The forces have equal magnitudes and are separated by 120∘.
Using the formula for the resultant of two vectors:
FR=√F2+F2+2F⋅F⋅cos(120∘)
Since cos(120∘)=−12:
FR=√F2+F2−F2=√F2=F
Step 6: Determine the Net Force
Since the resultant of any two forces will be equal in magnitude to the third force and they are symmetrically arranged, the net force acting on the point mass at the centroid will be zero.
Final Answer
The net force acting on the point mass of 5 kg placed at the centroid of the triangle is:
Net Force=0N
We have three masses (m1, m2, m3) of 1 kg each located at the vertices of an equilateral triangle with a side length of 3 m. The point mass (M) of 5 kg is placed at the centroid of the triangle.
For an equilateral triangle, the distance (r) from the centroid to any vertex can be calculated using the formula:
r=a√3
where a is the side length of the triangle. Here, a=3m.
r=3√3=√3m≈1.732m
The gravitational force F exerted by each mass on the point mass can be calculated using Newton's law of gravitation:
F=G⋅m⋅Mr2
where:
- G is the gravitational constant 6.674×10−11N m2/kg2
- m=1kg (mass at the vertex)
- M=5kg (mass at the centroid)
- r=√3m
F=6.674×10−11⋅1⋅5(√3)2
F=6.674×10−11⋅53
F=33.37×10−113≈11.12×10−11N
Each of the three forces F1,F2,F3 acts along the lines connecting the centroid to each vertex. Since the triangle is equilateral, the angle between any two forces is 120∘.
To find the resultant force FR acting on the point mass, we can use the vector addition of the forces. The forces have equal magnitudes and are separated by 120∘.
FR=√F2+F2+2F⋅F⋅cos(120∘)
Since cos(120∘)=−12:
FR=√F2+F2−F2=√F2=F
Since the resultant of any two forces will be equal in magnitude to the third force and they are symmetrically arranged, the net force acting on the point mass at the centroid will be zero.
The net force acting on the point mass of 5 kg placed at the centroid of the triangle is:
Net Force=0N
Topper's Solved these Questions
- GRAVITATION Book:AAKASH INSTITUTE ENGLISHChapter:GRAVITATION Exercise:ASSIGNMENT SECTION -A (Objective Type Questions (one option is correct))
Explore 50 Videos
- GRAVITATION Book:AAKASH INSTITUTE ENGLISHChapter:GRAVITATION Exercise:ASSIGNMENT SECTION -B (Objective Type Questions (one option is correct))
Explore 20 Videos
- GRAVITATION Book:AAKASH INSTITUTE ENGLISHChapter:GRAVITATION Exercise:ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
Explore 15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTE ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:ASSIGNMENT SECTION - D
Explore 9 Videos
- KINETIC THEORYBook:AAKASH INSTITUTE ENGLISHChapter:KINETIC THEORYExercise:EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
Explore 10 Videos
Similar Questions
Three equal masses of 1.5 kg each are fixed at the vertices of an equilateral triangle of side 1 m. What is the force acting on a particle of mass 1 kg placed at its centroid ?
View SolutionThree equal masses of mkg each are fixed at the vertices of an equilateral triangle ABC.
a. What is the force acting on a mass 2m placed at the centroid G of the triangle?
b. What is the force if the mass at the vertex A is doubled? Take AG=BG=CG=1m
View Solution
Knowledge Check
Three masses each of mass m are palced at the vertices of an equilateral triangles ABC of side l as shown in figure. The force acting on a mass 2m placed at the centroid O of the triangle is
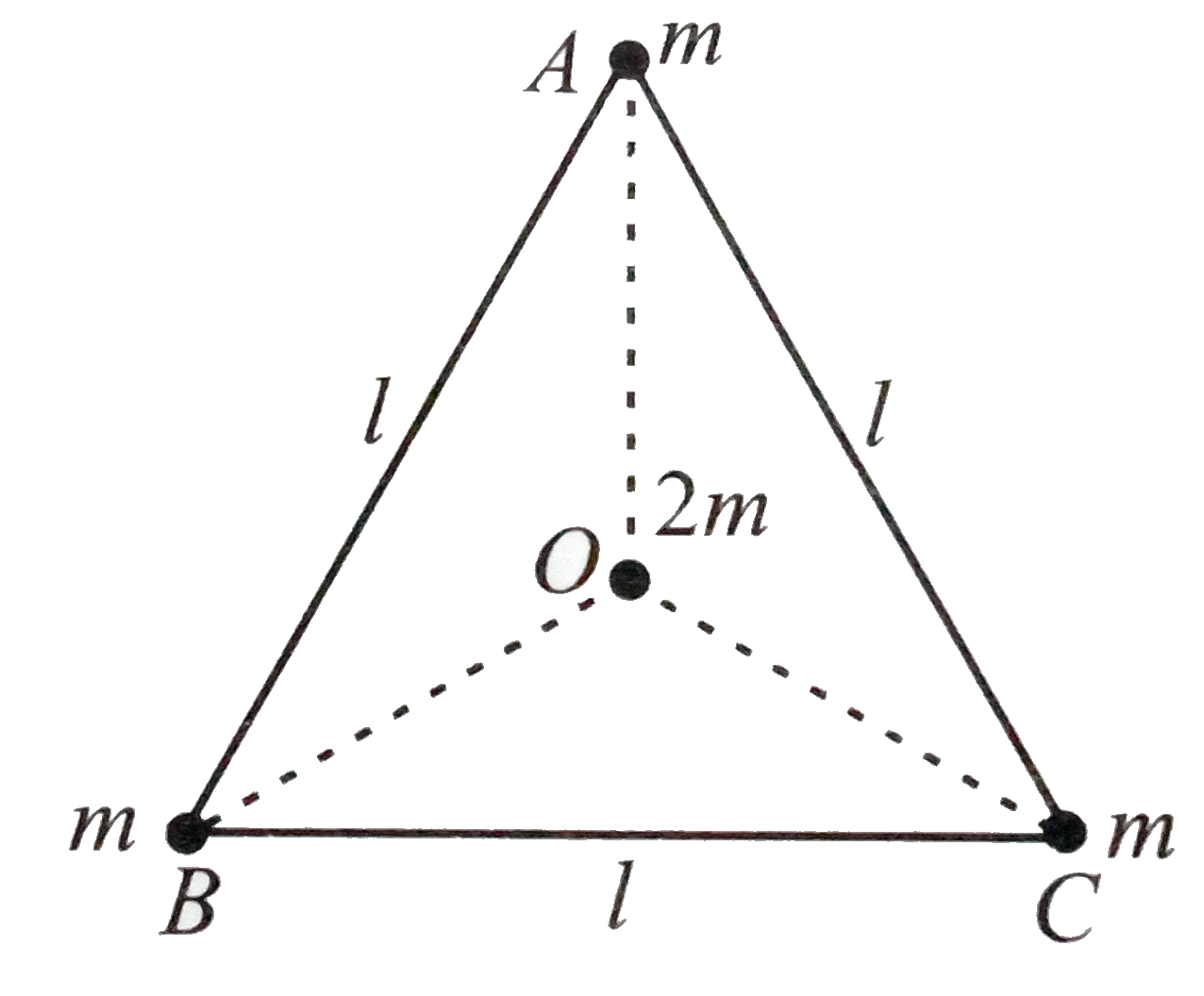 AzeroB3Gm2l2C5Gm2l2D7Gm2l2
AzeroB3Gm2l2C5Gm2l2D7Gm2l2Consider three charges q1,q2 and q3 each equal to q, at the vertices of an equilateral triangle of side l. What is the force on a charge Q placed at the centroid of the triangle?
A3Qq4πε0l2B2Qq4πε0l2CQq2πε0l2Dzero
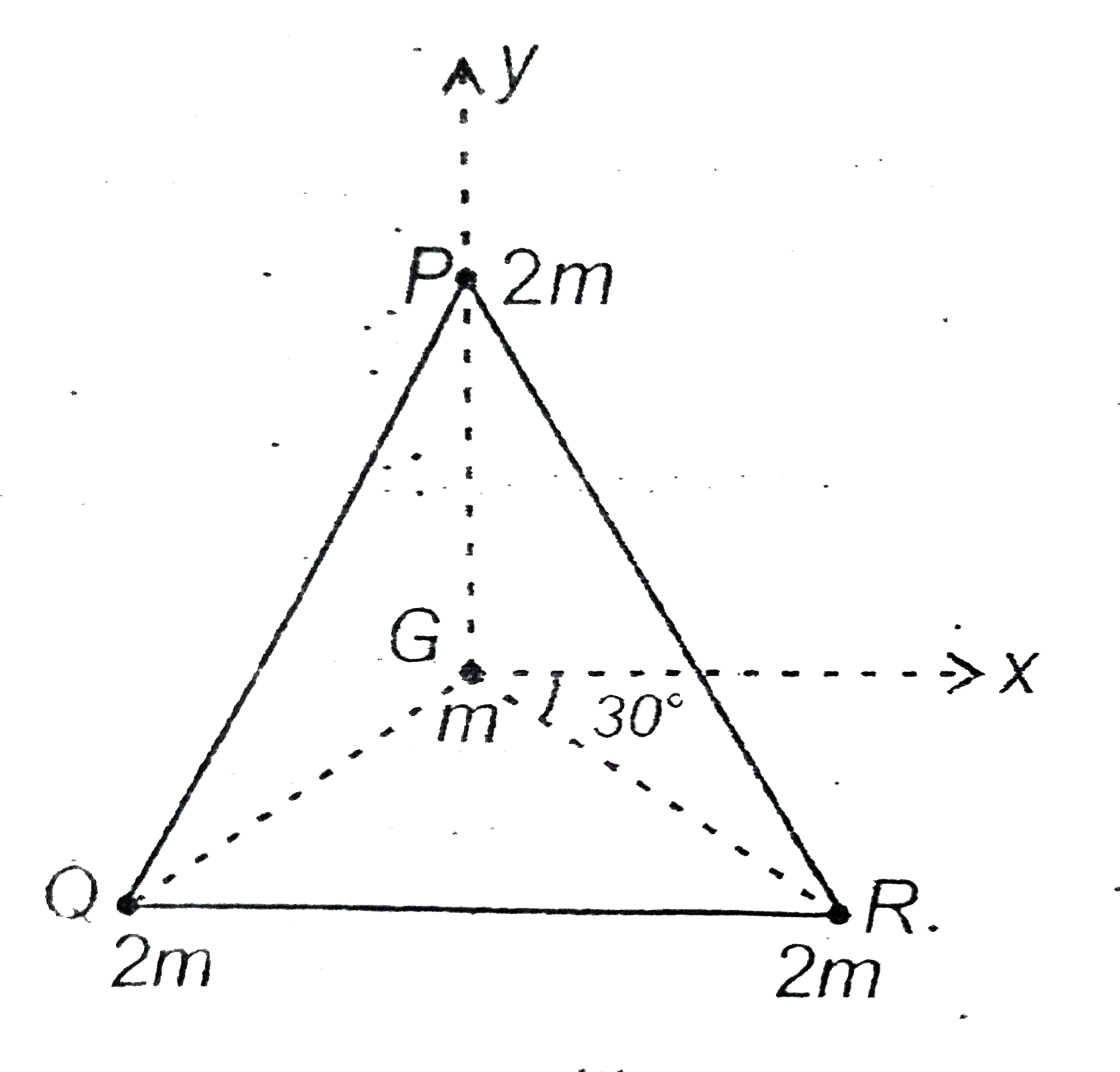
Three equal masses 2m each are placed at the vertices an equilateral triangle PQR
(i) What is the force acting on a mass m placed at the centroid G of the triangle ?
(ii) What is the force on mass m if the mass at the vertex P is quadrupled ?
Take PG = QG = RG = 1m
View SolutionThree charges of equal magnitude q is placed at the vertices of an equilateral triangle of side l. The force on a charge Q placed at the centroid of the triangle is
View SolutionThree equal masses of 1 kg each are placed at the vertices of an equilateral triangle of side 1 m, then the gravitational force on one of the masses due to other masses is (approx.)
View SolutionThree charges of equal magnitude q is placed at the vertices of an equilateral triangle of side l. The force on a charge Q placed at the centroid of the triangle is
View SolutionThree mass points each of mass m are placed at the vertices of an equilateral triangle of side 1. What is the gravitational field and potential due to the three masses at the centroid of the triangle ?
View SolutionThree point masses 'm' each are placed at the three vertices of an equilateral traingle of side 'a'. Find net gravitational force on any point mass.
View Solution
