A cubical block of iron, 5 cm on each side is floating in mercury taken in a vessel. What is the height of the block above mercury level.
From the law of floatation
Vbρb=VinρL
∴(5)3×(7.2)=(52×(13.6)
∴x=2.65cm
Then the height of the block above mercury level
=5cm−x=2.35cm
Similar Questions
A cubical block of iron 5 cm on each side is floating on mercury in a vessel. (i) what is the height of the block above mercury level ?
(ii) Water is poured in the vessel unitl it just covers the iron block. What is the height of water column . density of mercur 13.6gm/cm3. Density of iron 7.2 gm/cm3
View Solution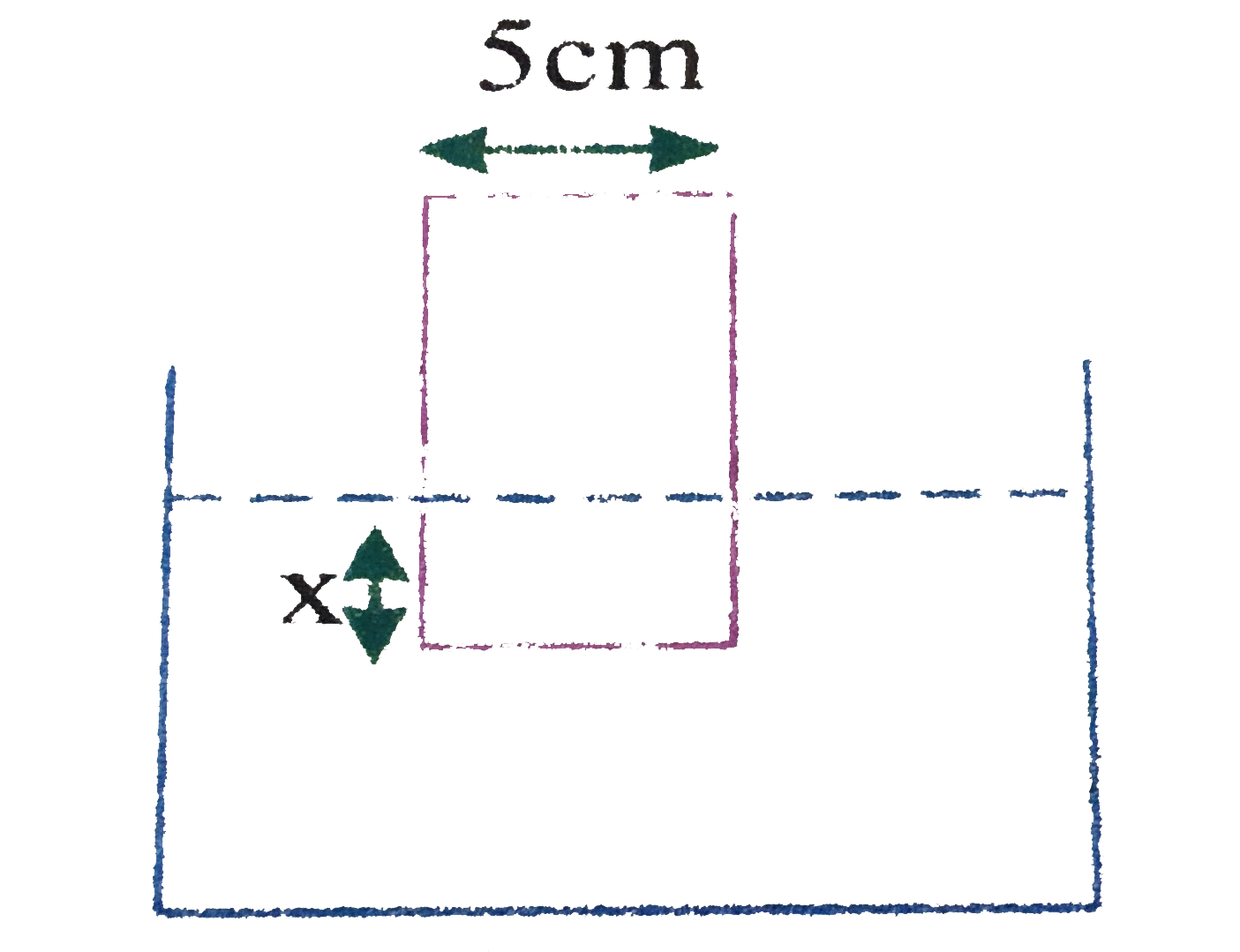
A cubical block of iron of side 5 cm is floating in mercury taken in a vessel. What is the height of the block above mercuery level.
(ρHg=13.6g/cm3,ρFe=7.2g/cm3)
View Solution
Knowledge Check
A cubical block of steel of each side equal to 1 is floating on mercury in vessel. The densities of steel and mercury are ρs and ρm. The height of the block above the mercury level is given by
Al(1+ρsρm)Bl(1−ρsρm)Cl(1+ρmρs)Dl(1−ρmρs)A cubical block of copper of side 10cm is floating in a vessel containing mercury. Water is poured into the vessel so that the copper block just gets submerged. The height of water column is
(ρHg=13.6g/cc,ρCu=7.3g/cc,ρwater=1gm/cc)A1.25 cmB2.5cmC5cmD7.5cmA cubical block of wood 10cm on a side floats at the interface between oil and water, as in fig. with its lower face 2cm below the interface. The intensity of the oli is 0.6gcm−3. The mass of the block is 1kg
 A340gB680gC80gD10g
A340gB680gC80gD10g
A cubical block of iron of side13.6cm is floating in mercury in a vessel .Water is poured in the vessel until it just covers the iron block. What is the height of water column? (ρHg=13.6gmcm3, ρFe=7.2gmcm3, ρH_2O=1gmcm3)
View SolutionA cubical block of steel of each side equal to 1 is floating on mercury in vessel. The densities of steel and mercury are ρs and ρm. The height of the block above the mercury level is given by
View Solution
A force F is applied on block A of mass M so that the tension in light string also becomes F when block B of mass m acquires an equilibrium state with respect to block A. find the force F. Give your answer in terms of m, M and g.
View SolutionA cubical block of wood 10 cm on a side floats at the interface between oil and water with its lower surface horizontal and 4 cm below the interface. The density of oil is 0.6gcm−3. The mass of block is
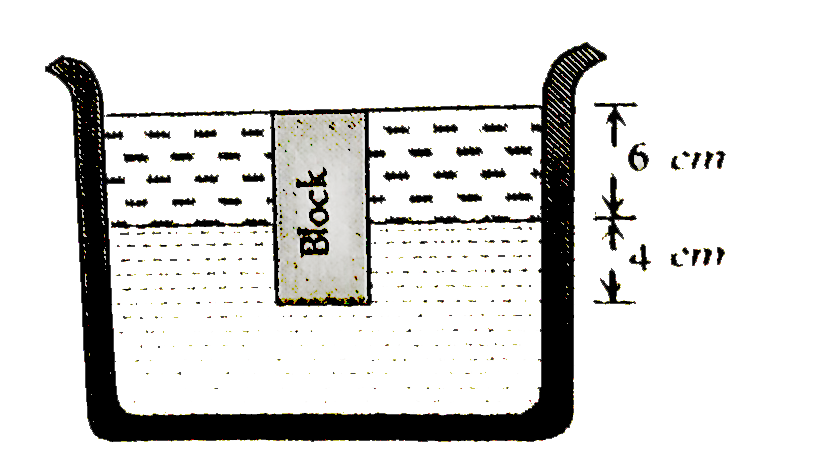
View SolutionA tank contains water on top of mercury as shown in figure. A cubical block of side 10 cm is in equilibrium inside the tank. The depth of the block inside mercury is (RD of the material of block =8.56, RD of mercury =13.6)

View Solution
