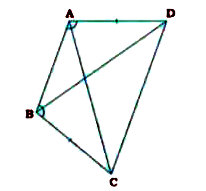
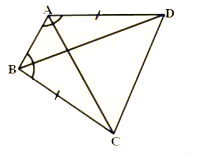
ABCD is a quadrilateral in which AD = BC and ∠DAB=∠CBA (see the given figure). Prove that ( i ) △ABD=△BAC,(ii)BD=ACand(iii)∠ABD=∠BAC
 Solution in Gujrati
Solution in Gujrati
The correct Answer is:∠BAC
Step by step video, text & image solution for ABCD is a quadrilateral in which AD = BC and angle DAB = angle CBA (see the given figure). Prove that ( i ) triangle ABD = triangle BAC, ( ii) BD = AC and (iii) angle ABD = angle BAC by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
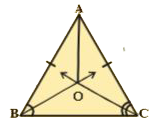
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠Band∠C intersect each other at O. Join A to O. Show that :
(i) OB = OC (ii) AO bisects ∠A
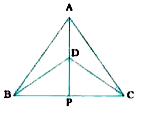
View Solution△ ABC and △ DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see the given figure). If AD is extended to intersect BC at P, show that, ( i ) △ABD=△ACD(ii)△ABP=△ACP (iii) AP bisects ∠ A as well as ∠ D. (iv) AP is the perpendicular bisector of BC
View SolutionThe total surface area of a cuboid with length 20 cm, breadth 15 cm and height 10 cm is ……… cm2.
View Solution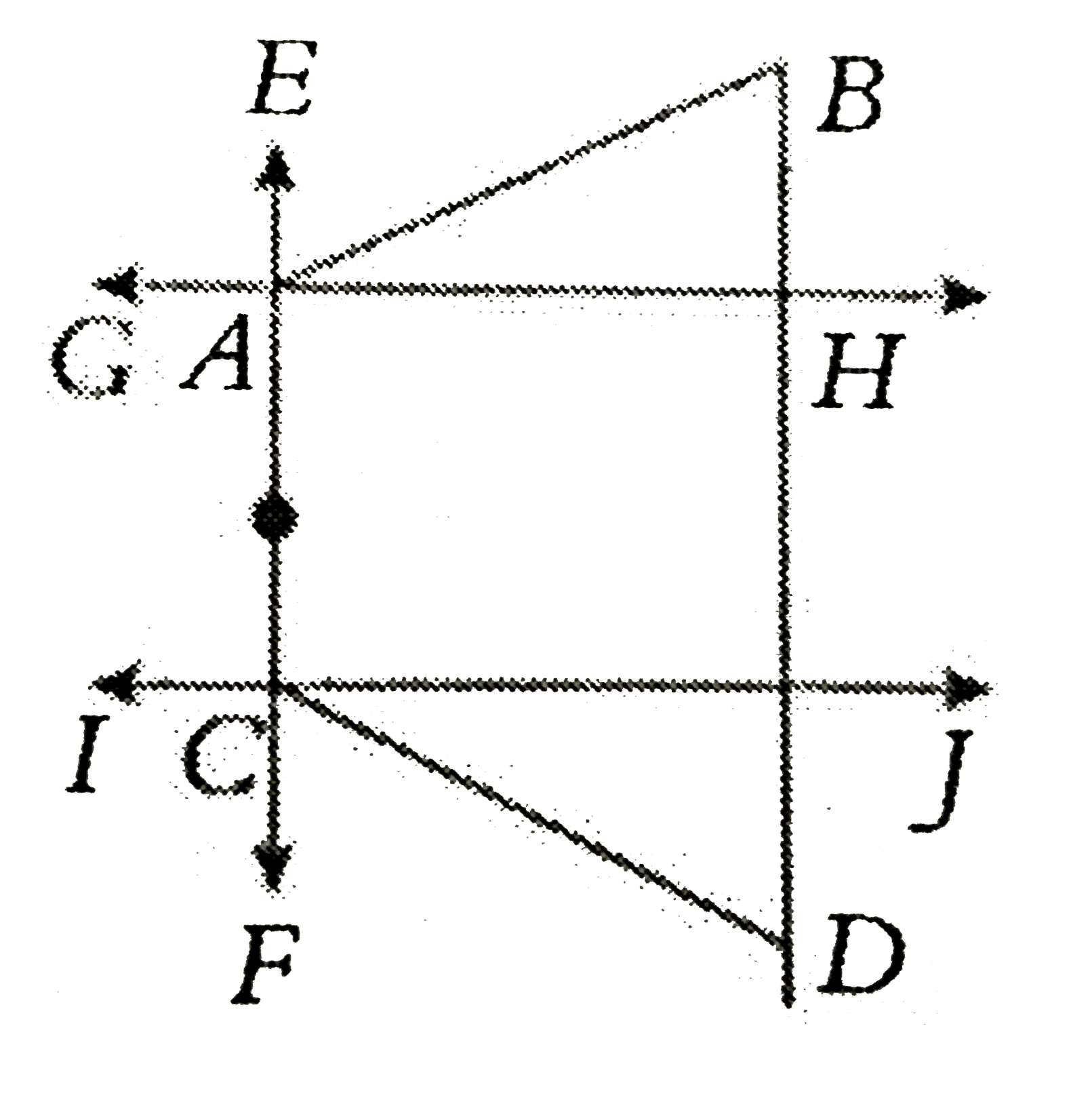
In the above figure, GH∣∣IJ and AC∣∣BD,AB and CD are bisectors of ∠EAH and ∠FCJ respectively. Find the ∠ABD+∠BDC, if ∠BAC=3∠BDC.
View SolutionIn the figure above (not to scale), ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯CDandAD is the bisector of ∠BAE.AB=3cm and AC=5cm. Find CD.
View SolutionIn the following figure, AB and BC are equidistant from the centre 'O' of the Show that
(a) ABC is an isosceles triangle.
(b) OB bisects angle ABC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_X_C13_E02_006_Q01.png" width="80%"gt
View SolutionIn the given figure, AB is a diameter, O is the center of the circle and ∠OCB=50∘ then find ∠DBC.
View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionABCD एक चतुर्भुज है, जिसमें AD = BC और ∠DAB=∠CBA है। सिद्ध कीजिए कि
(i) ΔABD≅ΔBAC
(ii) BD=AC
(iii) ∠ABD=∠BAC

View SolutionΔABC में, AD∠BAC का समद्विभाजक है । जो BC से D पर मिलती है, तो सिद्ध करें कि ar(ΔABD)ar(ΔACD)=ABAC
View SolutionABCD is a quadrilateral in which AD = BC and∠DAB=∠CBA Prove that
(i)ΔABD≅ΔBAC
(ii) BD=AC
(iii)∠ABD=∠BAC

View SolutionABCD is a quadrilateral in which AD = BC and∠DAB=∠CBA Prove that
(i)ΔABD≅ΔBAC
(ii) BD=AC
(iii)∠ABD=∠BAC

View SolutionABCD is a quadrilateral in which AD = BC and∠DAB=∠CBA Prove that
(i)ΔABD≅ΔBAC
(ii) BD=AC
(iii)∠ABD=∠BAC
View Solution
