ABCD एक चतुर्भुज है, जिसमें AD = BC और ∠DAB=∠CBA है। सिद्ध कीजिए कि
(i) ΔABD≅ΔBAC
(ii) BD=AC
(iii) ∠ABD=∠BAC
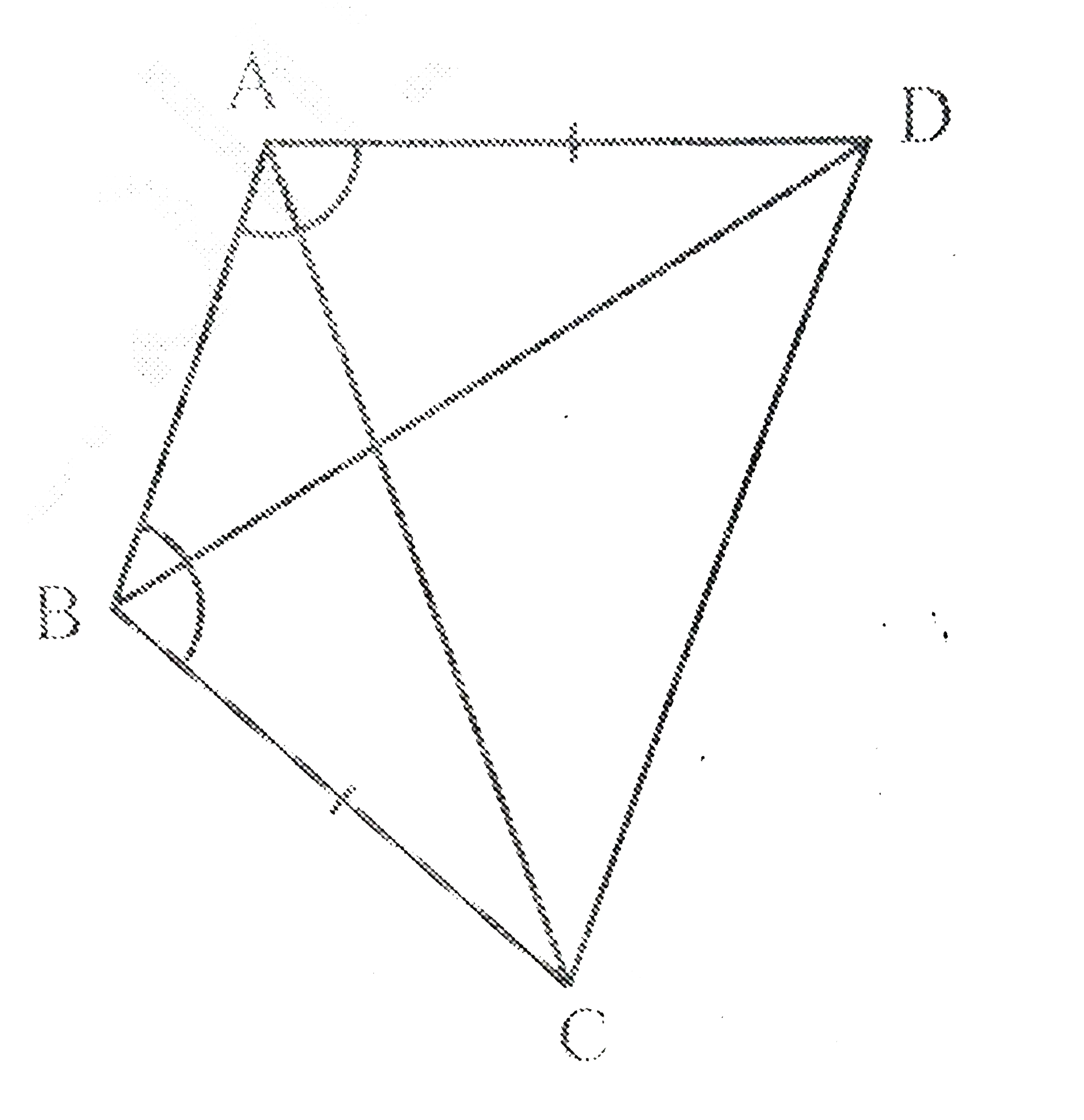
Step by step video & image solution for ABCD एक चतुर्भुज है, जिसमें AD = BC और angle DAB = angle CBA है। सिद्ध कीजिए कि (i) Delta ABD ~= Delta BAC (ii) BD= AC (iii) angle ABD = angle BAC by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिभुज BOOK - NCERT HINDICHAPTER - त्रिभुज EXERCISE - प्रश्नावली 7.2
8 Videos
- त्रिभुज BOOK - NCERT HINDICHAPTER - त्रिभुज EXERCISE - प्रश्नावली 7.3
5 Videos
- त्रिभुज BOOK - NCERT HINDICHAPTER - त्रिभुज EXERCISE - प्रश्नावली 7.5
4 Videos
- चतुर्भुज BOOK - NCERT HINDICHAPTER - चतुर्भुज EXERCISE - प्रश्नवली 8.2
7 Videos
- दो चारो वाले रैखिक समीकरण BOOK - NCERT HINDICHAPTER - दो चारो वाले रैखिक समीकरण EXERCISE - प्रश्नावली 4.4
2 Videos
Similar Questions
एक समद्विबाहु त्रिभुज ABC में जिसमें AB = AC है, ∠B और ∠C के समद्विभाजक परस्पर बिंदु O पर प्रतिच्छेद करते हैं। A और O को जोड़िए। दर्शाइए कि
(i) OB = OC
(ii) AO कोण A को समद्विभाजित करता है
View SolutionΔABC और ΔDBC एक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकार हैं कि A और D भुजा BC के एक ही ओर स्थित हैं। यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करे, तो दर्शाइए कि
(i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP कोण A और कोण D दोनों को समद्विभाजित करता है।
(iv) AP रेखाखंड BC का लम्ब समद्विभाजक है।
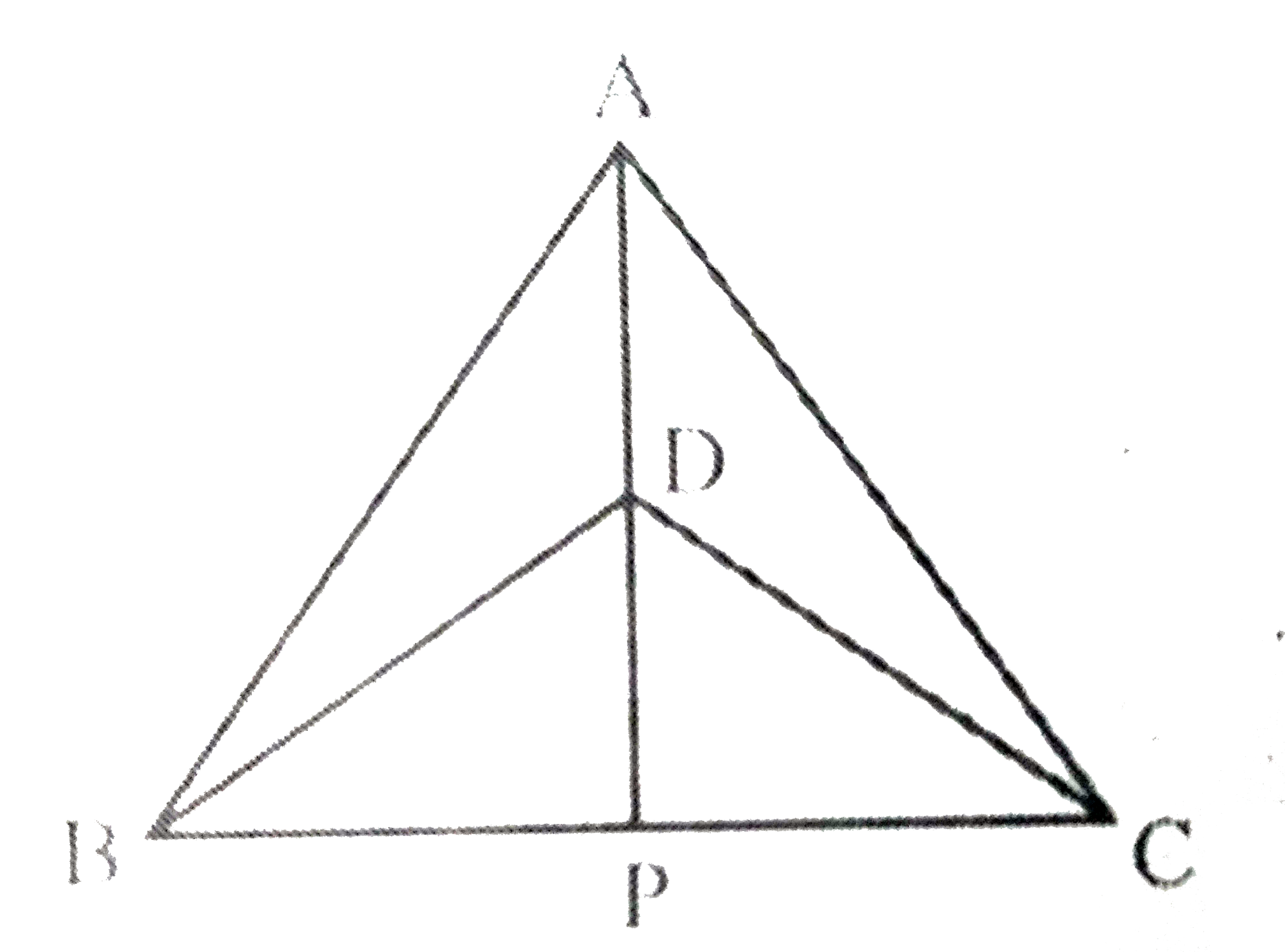
View SolutionABC एक त्रिभुज है। इसके अभ्यंतर में ऐसा बिंदु ज्ञात कीजिए जो ΔABC के तीनों शीर्षों से समदूरस्थ है।
View SolutionABCD एक चतुर्भुज है जिसमें P,Q,R और S क्रमश : भुजाओं AB,BC,CD और DA में मध्य - बिंदु है। AC उसका एक विकर्ण है। दर्शाइए कि
(i) SR∣∣AC और SR=12AC है
(ii) PQ=SR है |
(iii) PQRS एक समांतर चतुर्भुज है।
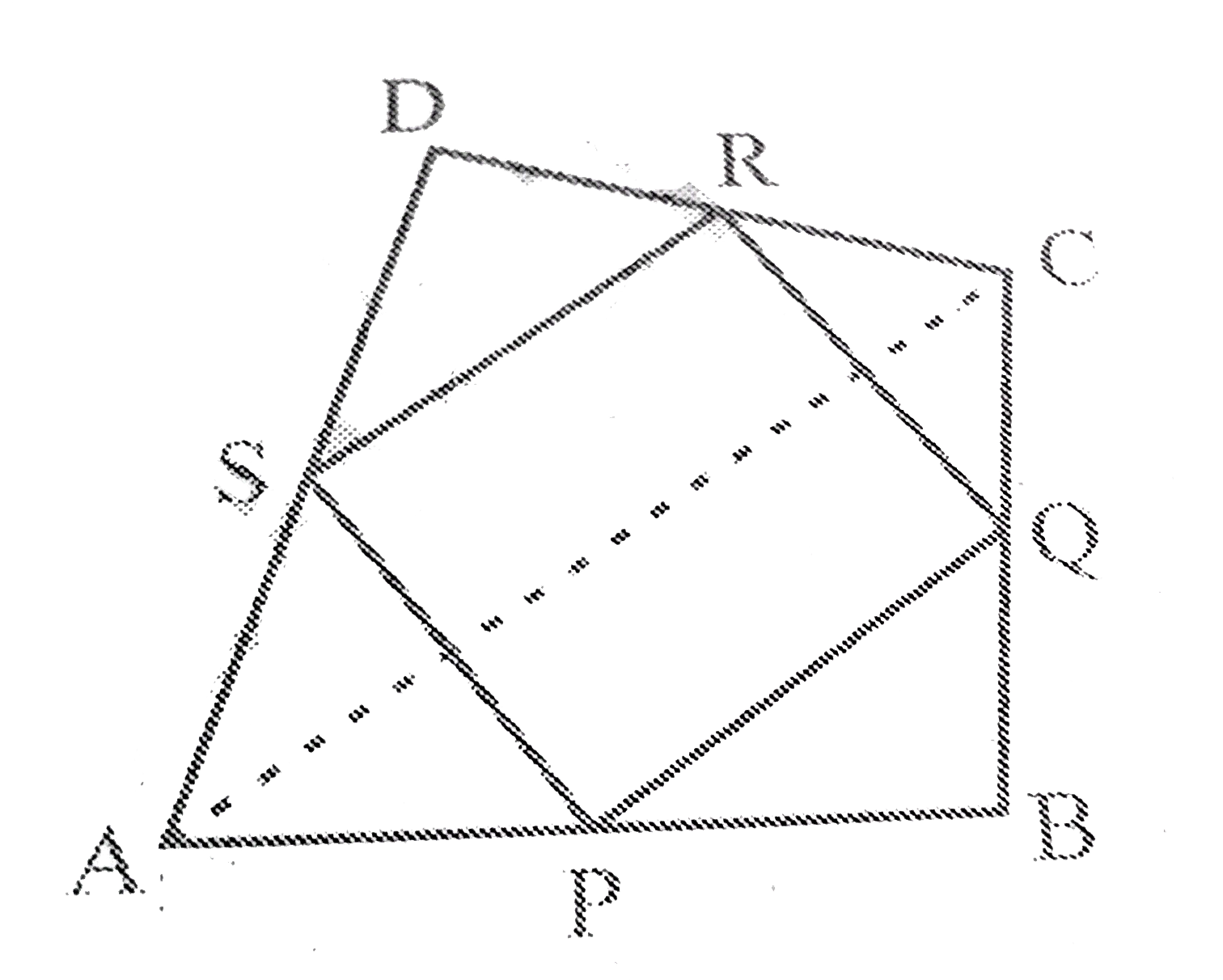
View Solution(i) एक चर वाले
(ii) दो चर वाले
समीकरण के रूप में y=3 का ज्यामितीय निरूपण कीजिए |
View Solution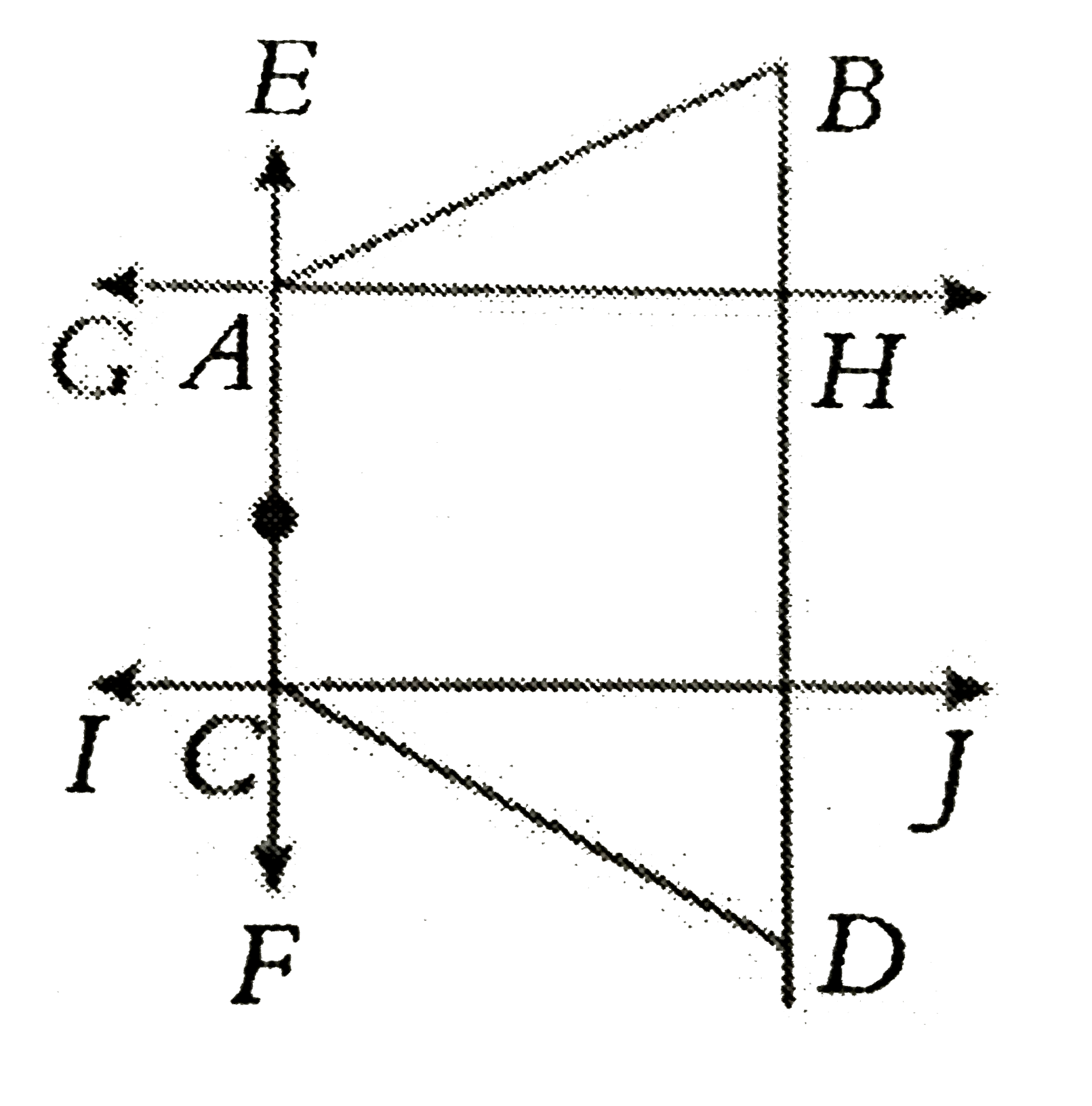
In the above figure, GH∣∣IJ and AC∣∣BD,AB and CD are bisectors of ∠EAH and ∠FCJ respectively. Find the ∠ABD+∠BDC, if ∠BAC=3∠BDC.
View SolutionIn the figure above (not to scale), ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯CDandAD is the bisector of ∠BAE.AB=3cm and AC=5cm. Find CD.
View SolutionMatch the following Column A to Column B

View SolutionΔABC में, AD∠BAC का समद्विभाजक है । जो BC से D पर मिलती है, तो सिद्ध करें कि ar(ΔABD)ar(ΔACD)=ABAC
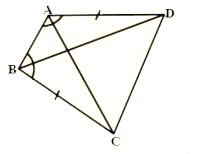
View SolutionABCD is a quadrilateral in which AD = BC and∠DAB=∠CBA Prove that
(i)ΔABD≅ΔBAC
(ii) BD=AC
(iii)∠ABD=∠BAC
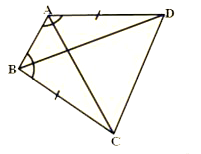
View SolutionABCD is a quadrilateral in which AD = BC and∠DAB=∠CBA Prove that
(i)ΔABD≅ΔBAC
(ii) BD=AC
(iii)∠ABD=∠BAC
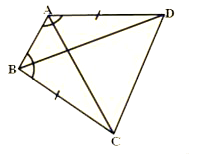
View SolutionABCD is a quadrilateral in which AD = BC and∠DAB=∠CBA Prove that
(i)ΔABD≅ΔBAC
(ii) BD=AC
(iii)∠ABD=∠BAC
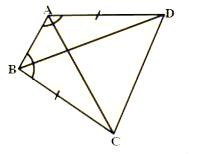
View SolutionABCD is a quadrilateral in which AD = BC and∠DAB=∠CBA Prove that
(i)ΔABD≅ΔBAC
(ii) BD=AC
(iii)∠ABD=∠BAC
View SolutionABCD is a quadrilateral in which AD = BC and ∠DAB=∠CBA (see the given figure). Prove that ( i ) △ABD=△BAC,(ii)BD=ACand(iii)∠ABD=∠BAC
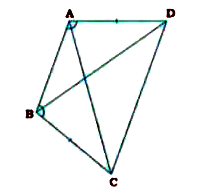
View Solutionत्रिभुज ABD में ∠DAB , बिंदु A से DB पर लब AC खींचा गया है । सिद्ध कीजिए : AD2=BD×CD
View Solution
