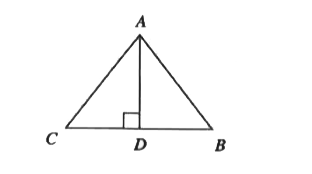
AD is an altitude of an equilateral triangle ABC. On AD as base, another equilateral triangle ADE is constructed. Prove that Area ( triangle ADE ): Area ( triangle ABC )=3:4.
Step by step video & image solution for AD is an altitude of an equilateral triangle ABC. On AD as base, another equilateral triangle ADE is constructed. Prove that Area ( triangle ADE ): Area ( triangle ABC )=3:4. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
What is the area of equilateral triangle if the base BC = 6 ?
 A9√3B18√3C26√3D30√3
A9√3B18√3C26√3D30√3
Construct an equilateral triangle ABC with side 6 cm. Draw a circle circumscribing the triangle ABC.
View SolutionFind the area of an equilateral triangle having altitude h cm.
View SolutionABC is an equilateral triangle .If AD bisects angle A, Prove that AD is perpendicular bisector of BC .
View SolutionConstruct an equilateral triangle whose altitude is 4 cm.
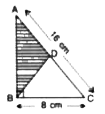
View SolutionThe given figure shows a right angled triangle ABC and an equilateral triangle BCD.
Find the area of the shaded portion.
View SolutionProve that the area of equilateral triangle described on the side of a square is half the area of the equilateral triangle described on its diagonal.
View SolutionProve that the area of equilateral triangle described on the side of a square is half the area of the equilateral triangle described on its diagonal.
View Solution