Question

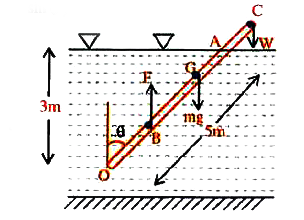
A uniform rod is of length 6 m and mass 12 kg. One end of this rod is hinged to a point at a depth 3 m below the free surface of water. Find (1) the weight to be suspended at the other end, so that mof length of the rod remains immersed in water, (ii) the magnitude and direction of the reaction at the hinge (spgravity of the material of the rod 0.5)

Explanation

The rod makes angle with the vertical shape cose`theta=(3)/(5)` and sin `theta=(4)/(3)` Let .a. be the area of cross section of the rod.
`therefore` weight of the rod mg (6) 500 g N, Force of buoyancy F = (5a) 1000 g N
IF W N be the weight at the end (required), then taking moments about the hinge and equating it to zero
for rotatory equilibrium),(5000ag)2.5 sin `theta`)-(3000 ag)3 sin `theta`-W (6 sin `theta`)=0
Since sin `thetanetheta` ,so cancelling ag sin `theta` throughtout.
12500-9000-`(6W)/(ag)=3500implies(w)/(g)=(3500)/(6)a`

Now, the mass of the rod=12 kg `implies(6a)xx500=12impliesa=(1)/(250)m^(2)`
`therefore (W)/(g)=(3500)/(6xx250)=2.33 kg` wt. or W=22.837 N
ii)Now, upthrust F=`5000 xx(1)/(250)` g=20 gN
IFR be the verical reaction (up) at the hinge, then for vertical equlibrium of the rod, R+F-mg - W=0
`impliesR+20g-12g-2.33g=0implies`R=-5.67kg 2t.(or) -55.57N
The -Ve sign implies that ,the reaction is downwards of magnitude 55.57N