A cubical block of iron, 5cm on each side is floating in mercury taken in a vessel. What is the height of the block above mercury level.
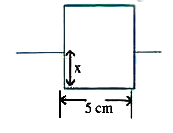
Then, the height of the block above mercury level =5cm-x=2.35 cm
Topper's Solved these Questions
- FLUID MECHANICSBOOK - AAKASH SERIESCHAPTER - FLUID MECHANICSEXERCISE - Test your self
6 Videos
- FLUID MECHANICSBOOK - AAKASH SERIESCHAPTER - FLUID MECHANICSEXERCISE - Short answer type questions
13 Videos
- FLUID MECHANICSBOOK - AAKASH SERIESCHAPTER - FLUID MECHANICSEXERCISE - ADDITIONAL PRACTICE SHEET (ADVANCED) (Straight Objective Type Questions)
5 Videos
- EXPANSION OF SOLIDS BOOK - AAKASH SERIESCHAPTER - EXPANSION OF SOLIDS EXERCISE - Questions for Descriptive Answers
5 Videos
- FRICTION BOOK - AAKASH SERIESCHAPTER - FRICTION EXERCISE - ADDITIONAL PRACTICE EXERCISE PRACTICE SHEET (ADVANCED) (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
1 Videos
Similar Questions
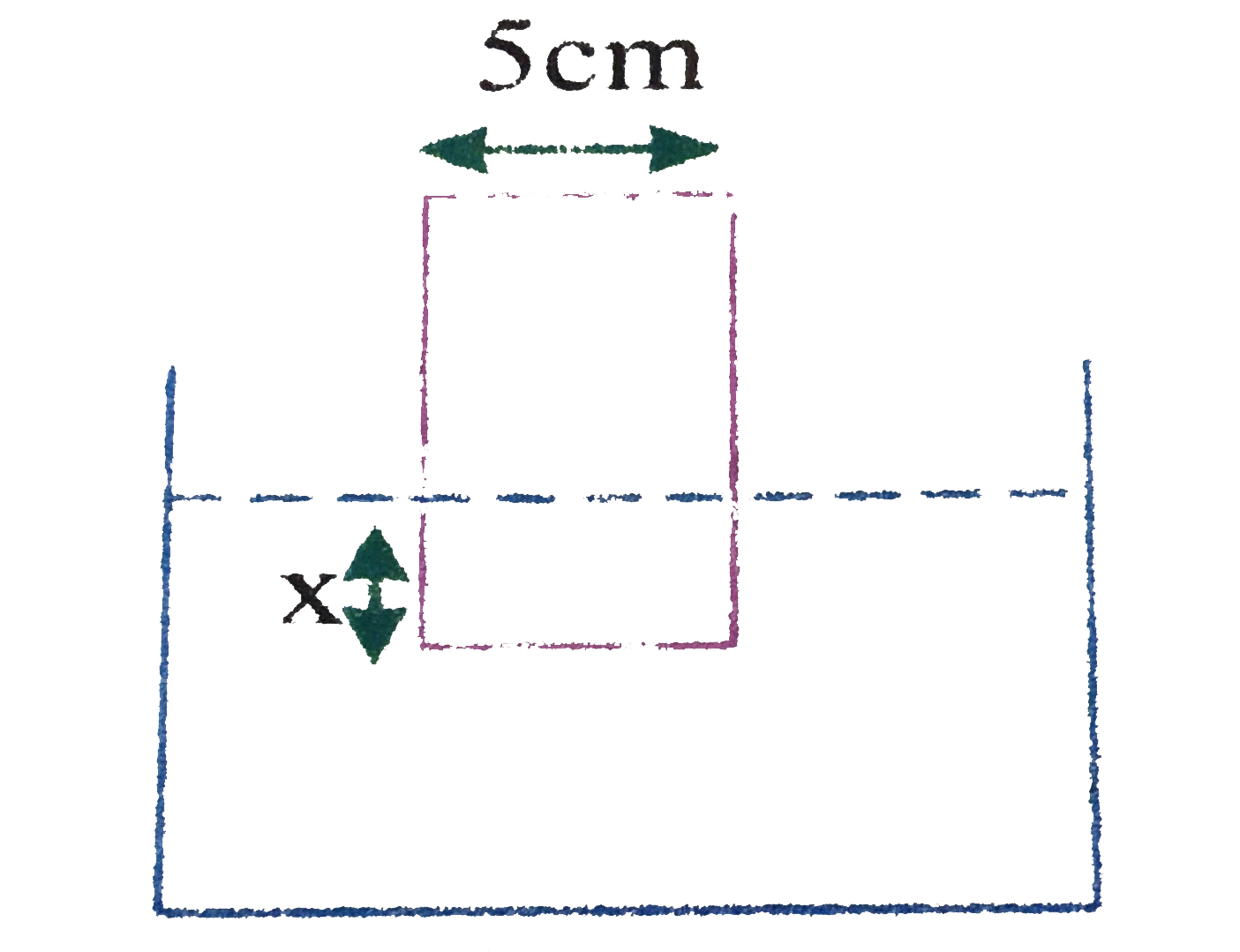
A cubical block of iron of side 5 cm is floating in mercury taken in a vessel. What is the height of the block above mercuery level.
(ρHg=13.6g/cm3,ρFe=7.2g/cm3)
View SolutionA cubical block of iron 5 cm on each side is floating on mercury in a vessel. (i) what is the height of the block above mercury level ?
(ii) Water is poured in the vessel unitl it just covers the iron block. What is the height of water column . density of mercur 13.6gm/cm3. Density of iron 7.2 gm/cm3
View Solution
Knowledge Check
A cubical block of steel of each side equal to 1 is floating on mercury in vessel. The densities of steel and mercury are ρs and ρm. The height of the block above the mercury level is given by
Al(1+ρsρm)Bl(1−ρsρm)Cl(1+ρmρs)Dl(1−ρmρs)A cubical block of copper of side 10cm is floating in a vessel containing mercury. Water is poured into the vessel so that the copper block just gets submerged. The height of water column is
(ρHg=13.6g/cc,ρCu=7.3g/cc,ρwater=1gm/cc)A1.25 cmB2.5cmC5cmD7.5cmA cubical block of wood 10cm on a side floats at the interface between oil and water, as in fig. with its lower face 2cm below the interface. The intensity of the oli is 0.6gcm−3. The mass of the block is 1kg
 A340gB680gC80gD10g
A340gB680gC80gD10g
A cubical block of steel of each side equal to 1 is floating on mercury in vessel. The densities of steel and mercury are ρs and ρm. The height of the block above the mercury level is given by
View SolutionA cubical block of iron of side13.6cm is floating in mercury in a vessel .Water is poured in the vessel until it just covers the iron block. What is the height of water column? (ρHg=13.6gmcm3, ρFe=7.2gmcm3, ρH_2O=1gmcm3)
View SolutionA cubical block of mass 2 kg with each side of 2 cm is lying on the ground. What will be the pressure exerted by the block on the ground?
(Take g=9.8m/s2)
View SolutionA cubical block of side 10 cm floats at the interface of an oil and water. The pressure above that of atmosphere at the lower face of the block is
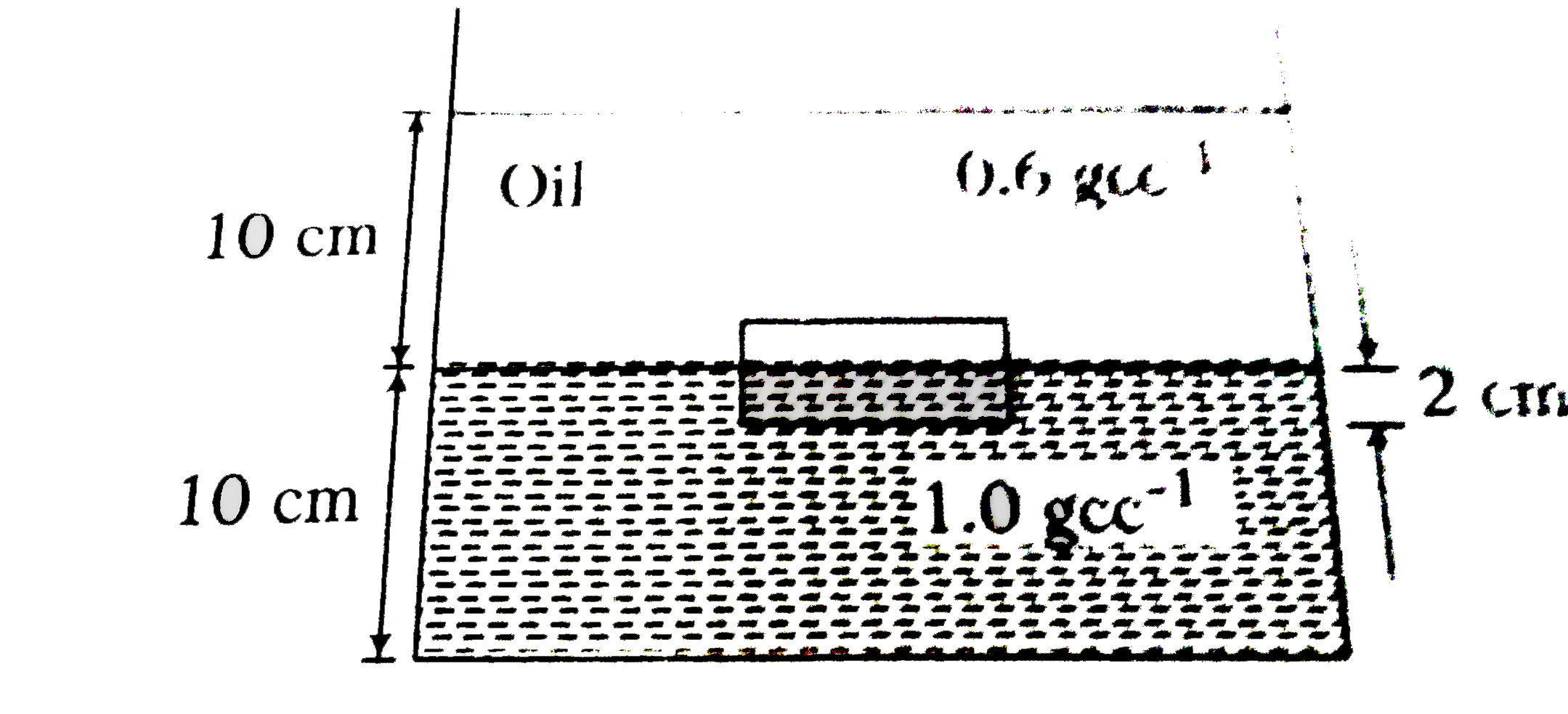
View SolutionA cubical block of side 10 cm floats at the interface of an oil and water. The pressure above that of atmosphere at the lower face of the block is
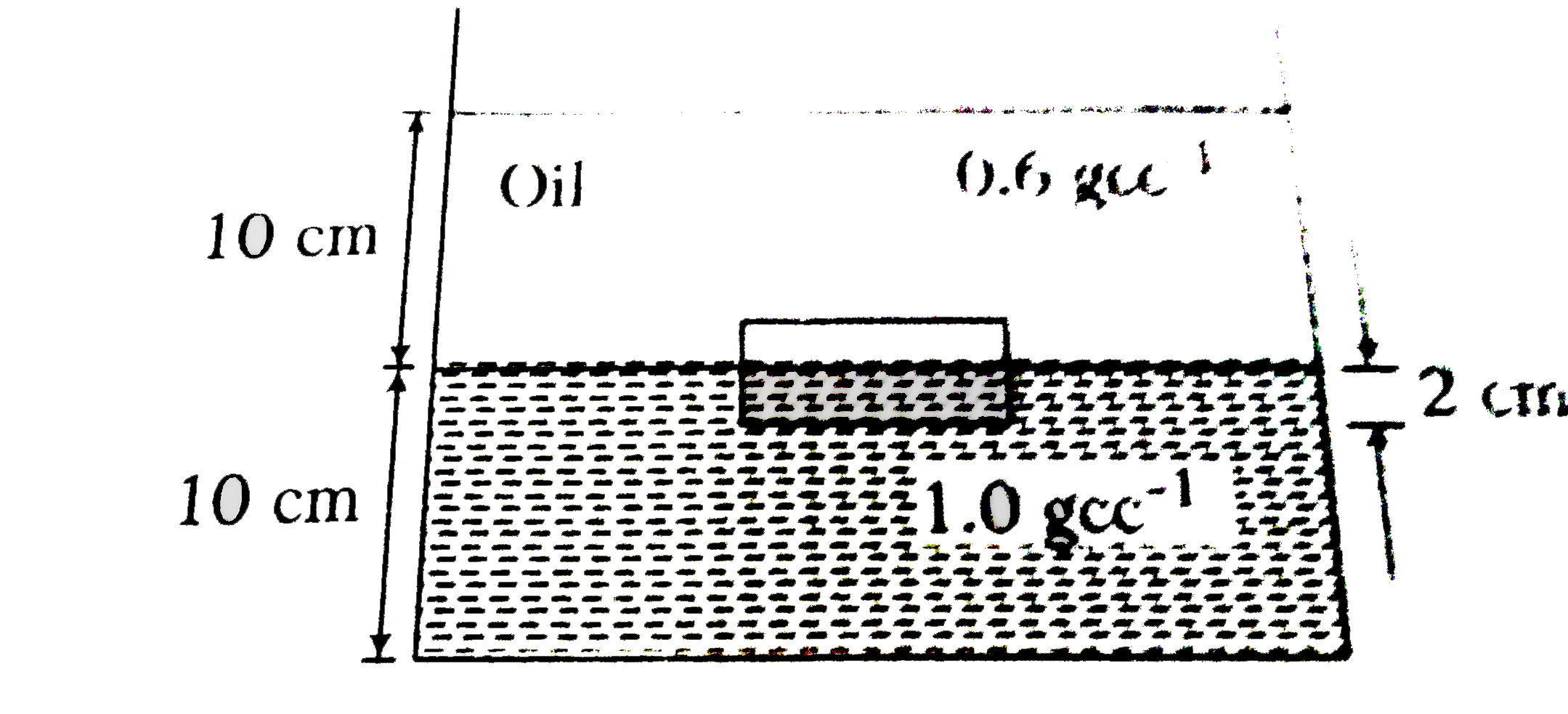
View Solution
