Velocity of particle at time t = 0 is 2ms−1 . A constant acceleration of 2ms−2 acts on the particle for 1 second at an angle of 60∘ with its nitnial velocity. Find the magnitude of velocity at the end of 1second.
√3m/s
2√3m/s
4m/s
8m/s
The correct Answer is:B
Topper's Solved these Questions
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (RELATIVE VELOCITY)
16 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (A BOAT IN A RIVER)
10 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (PARALLELOGRAM LAW, TRIANGLE LAW, POLYGON LAW)
14 Videos
- RAY OPTICS BOOK - AAKASH SERIESCHAPTER - RAY OPTICS EXERCISE - EXERCISE III
64 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) Integer Type Questions
7 Videos
Similar Questions
Velocity of particle at time t=0 is 2ms−1.A constant acceleration of 2ms−2 act on the particle for 1 second at an angle of 60∘ with its initial velocity .Find the magnitude velocity and displacement of the particle at the end of t=1s.
View SolutionVelocity of a particle at time t=0is2m/s. A constant acceleration of 2ms2 acts on the particle for 2s at an angle of 60∘ with its initial velocity. Find the magnitude of velocity and displacement of particle at the end of t=2s.
View Solution
Knowledge Check
Velocity of a particle at time t=0 is 2ms−1. A constant acceleration of 2ms−2 acts on the particle for 1second at an angle of 60∘ with its initial velocity. Find the magnitude of velocity at the end of 1second.
A√3m/sB2√3m/sC4m/sD8m/sAn object has a velocity, v=(2ˆi+4ˆj)ms−1 at time t=0s. It undergoes a constant acceleration a=(ˆi−3ˆj)ms−2 for 4s. Then
(i) Find the coordinates of the object if it is at origin at t=0
(ii) Find the magnitude of its velocity at the end of 4s.A10cm , 8m , ⇒v=6ˆi−8ˆjB16cm , 18m , ⇒v=6ˆi−8ˆjC16cm , 8m , ⇒v=2ˆi−8ˆjD16cm , 8m , ⇒v=6ˆi−8ˆjA particle has an initial velocity of 5.5ms−1 due east and a constant acceleration of 1ms−2 due west. The distance covered by the particle in sixth second of its motion is.
A0B0.25 mC0.5 mD0.75 m
Velocity of a particle at time t=0 is 2ˆi m/s. A constant acceleration of 2ms2 acts on the particle for 2s at an angle of 60∘ with its initial velocity. Find the magnitude of velocity and displacement of particle at the end of t=2s.
View SolutionAn object has a velocity, v=(2ˆi+4ˆj)ms−1 at time t=0s. It undergoes a constant acceleration a=(ˆi−3ˆj)ms−2 for 4s. Then
(i) Find the coordinates of the object if it is at origin at t=0
(ii) Find the magnitude of its velocity at the end of 4s.
View SolutionA particle moving with a velocity equal to 0.4ms−1 is subjected to an acceleration of 0.15ms−2 for 2 seconds in a direction at right angles to the direction of motion. The magnitude of the final velocity is
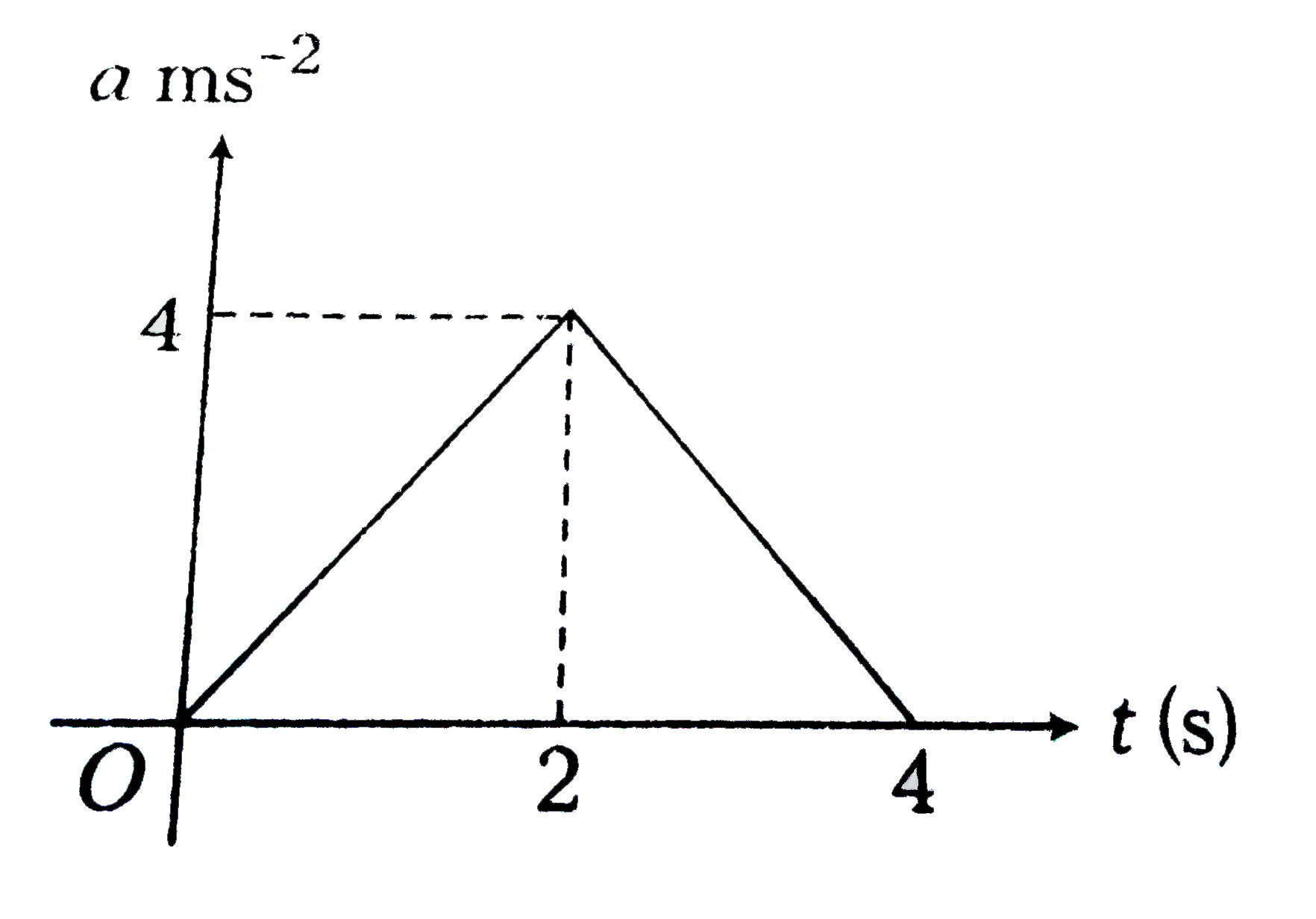
View SolutionAcceleration - time graph of a particle moving in a straight line is shown in figure. Velocity of particle at time t = 0 is 2ms−1. Find velocity at the end of fourth second.
View SolutionA particle is projected from ground at an angle 45∘ with initial velocity 20√2ms−1.The magnitude of average velocity in a timer interval from t=0 to t=3s in ms−1 is
View Solution
