Velocity of particle at time t=0 is 2ms−1.A constant acceleration of 2ms−2 act on the particle for 1 second at an angle of 60∘ with its initial velocity .Find the magnitude velocity and displacement of the particle at the end of t=1s.
√3m/s
2√3m/s
4m/s
8m/s
The correct Answer is:B
To solve the problem, we need to find the magnitude of the velocity and the displacement of the particle at the end of t=1 second, given that the initial velocity is 2m/s and a constant acceleration of 2m/s2 acts at an angle of 60∘ with the initial velocity.
1. Identify the initial conditions:
- Initial velocity u=2m/s
- Acceleration a=2m/s2
- Angle θ=60∘
- Time t=1s
2. Resolve the acceleration into components:
- Acceleration in the x-direction:
ax=acos(60∘)=2⋅12=1m/s2
- Acceleration in the y-direction:
ay=asin(60∘)=2⋅√32=√3m/s2
3. Calculate the final velocity in the x-direction:
- The initial velocity in the x-direction ux=2m/s
- Using the equation:
vx=ux+axt=2+1⋅1=3m/s
4. Calculate the final velocity in the y-direction:
- The initial velocity in the y-direction uy=0m/s
- Using the equation:
vy=uy+ayt=0+√3⋅1=√3m/s
5. Calculate the magnitude of the resultant velocity:
- The magnitude of the velocity v is given by:
v=√v2x+v2y=√32+(√3)2=√9+3=√12=2√3m/s
6. Calculate the displacement in the x-direction:
- Using the formula for displacement:
sx=uxt+12axt2=2⋅1+12⋅1⋅12=2+12=2.5m
7. Calculate the displacement in the y-direction:
- Using the formula for displacement:
sy=uyt+12ayt2=0+12⋅√3⋅12=√32m
8. Calculate the magnitude of the resultant displacement:
- The magnitude of the displacement s is given by:
s=√s2x+s2y=
⎷(2.5)2+(√32)2=√6.25+34=√6.25+0.75=√7m
Final Answers:
- Magnitude of velocity at t=1s: 2√3m/s
- Displacement at t=1s: √7m
- Initial velocity u=2m/s
- Acceleration a=2m/s2
- Angle θ=60∘
- Time t=1s
- Acceleration in the x-direction:
ax=acos(60∘)=2⋅12=1m/s2
- Acceleration in the y-direction:
ay=asin(60∘)=2⋅√32=√3m/s2
- The initial velocity in the x-direction ux=2m/s
- Using the equation:
vx=ux+axt=2+1⋅1=3m/s
- The initial velocity in the y-direction uy=0m/s
- Using the equation:
vy=uy+ayt=0+√3⋅1=√3m/s
- The magnitude of the velocity v is given by:
v=√v2x+v2y=√32+(√3)2=√9+3=√12=2√3m/s
- Using the formula for displacement:
sx=uxt+12axt2=2⋅1+12⋅1⋅12=2+12=2.5m
- Using the formula for displacement:
sy=uyt+12ayt2=0+12⋅√3⋅12=√32m
- The magnitude of the displacement s is given by:
s=√s2x+s2y=
⎷(2.5)2+(√32)2=√6.25+34=√6.25+0.75=√7m
- Magnitude of velocity at t=1s: 2√3m/s
- Displacement at t=1s: √7m
Topper's Solved these Questions
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - MOTION IN A STRAIGHT LINE
59 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- ATOMSBOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE
21 Videos
Similar Questions
Velocity of a particle at time t=0 is 2ˆi m/s. A constant acceleration of 2ms2 acts on the particle for 2s at an angle of 60∘ with its initial velocity. Find the magnitude of velocity and displacement of particle at the end of t=2s.
View SolutionA particle of mass 1 kg has a velocity of 2m/s. A constant force of 2N acts on the particle for 1s in a direction perpendicular to its initial velocity. Find the velocity and displacement of the particle at the end of 1 s.
View SolutionVelocity and acceleration of a particle at time t=0are u=(2ˆi+3ˆj)m/sanda=(4ˆi+3ˆj)m/s2 respectively. Find the velocity and displacement if particle at t=2s.
View SolutionIf acceleration a(t)=3t2 and initial velocity u=0 m/s , then the velocity of the particle after time t=4 s
View SolutionVelocity of a particle at any time t is v=(2ˆi+2tˆj)m/s. Find acceleration and displacement of particle at t=1s. Can we apply v=u+at or not?
View SolutionA particle moves in the x-y plane with a constant acceleration of 1.5m/s2 in the direction making an angle of 37∘ with the x-axis.
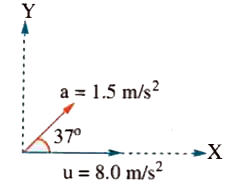
At t=0 the particle is at the origin and its velocity is 8.0m/s along the x- aixs . Find the velocity and the position of the particle at t = 4.0s.
View SolutionA particle movesin the X-Y plane with a constasnt acceleration of 1.5ms2 in the direction making an angle of 370 with the X-axis.At t=0 the particle is at the orign and its velocity is 8.0 m/s along the X-axis. Find the velocity and the position of the particle at t=4.0 s.

View SolutionThe velocity of a particle varies with its displacement as v=(√9−x2)ms−1.
Find the magnitude of the maximum acceleration of the particle.
View SolutionThe velocity of a particle is given by v=(2t2−3t+10)ms−1. Find the instantaneous acceleration at t = 5 s.
View SolutionA particle has initial velocity 4i+4jms−1 and an acceleration −0.4ims−2, at what time will its speed bbe 5ms−1?
View Solution
