A particle starts from point A moves along a straight line path with an acceleration given by a=p−qx where p, q are constant and x is distance from point A. the particle stops at point B. The maximum velocity of the particle is
pq
p√q
qp
√qp
The correct Answer is:B
Similar Questions
A particle starts from point A, moves along a straight line path with an acceleration given by a=2(4−x) where x is distance from point A. The particle stops at point B for a moment. Find the distance AB(in m). (All values are in S.I. Units)
View SolutionA particle starts from point A, moves along a straight line path with an accleration given by a=2(4−x) where x is distance from point A. The particle stops at point B for a moment. Find the distance AB (in m). (All values are in S.I. units)
View Solution
Knowledge Check
A particle starts from point A moves along a straight line path with an acceleration given by a=p−qx where p, q are connected and x is distance from point A . The particle stops at point B. The maximum velocity of the particle is
ApqBp√qCqpD√qpA particle starts from point A moves along a straight line path with an acceleration given by a = p - qx where p, q are connected and x is distance from point A . The particle stops at point B. The maximum velocity of the particle is
ApqBp√qCqpD√qpA particle starting from rest moves along a straight line with constant acceleration for this velocity displacement graph will have the form-
A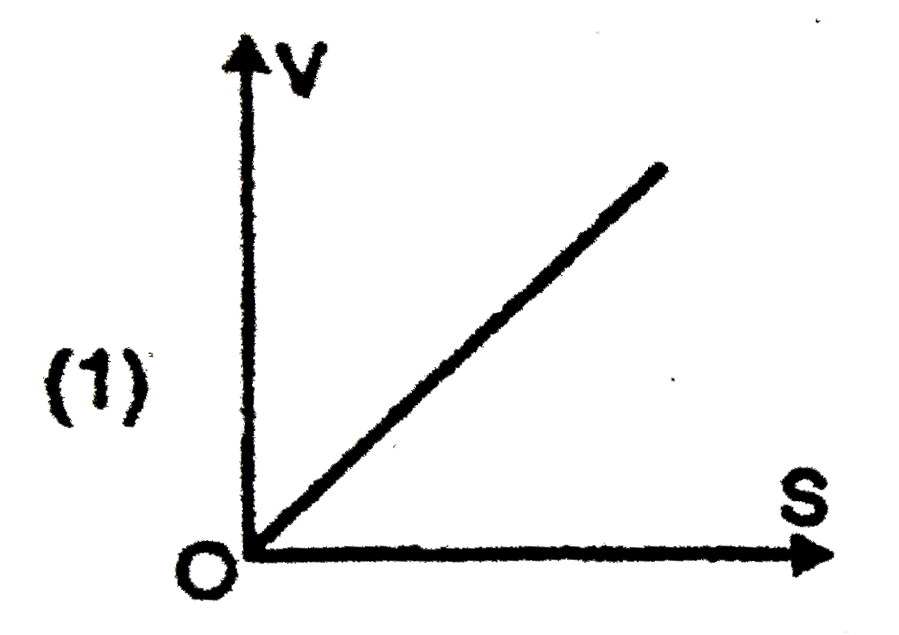 B
B C
C D
D
A particle starts from point A, moves along a straight line path with an accleration given by a=2(4−x) where x is distance from point A. The particle stops at point B for a moment. Find the distance AB (in m). (All values are in S.I. units)
View SolutionA particle starts from rest at t=0 and moves along a straight line with a variable acceleration given by a (t)=(3t+1)ms−2 ,where t],[ is in seconds.The velocity of the particle at t=4s is
View SolutionA particle starting from rest moves along a straight line with constant acceleration for this velocity displacement graph will have the form-
View SolutionA particle starts from the origin with a velocity of 2 cm/s and moves along a straight line. If the acceleration of the particle at a distance x cm from the origin be (2x−32)cms2, find the velocity of the particle at a distance 7 cm from the origin.
View SolutionA particle moves in a straight line so that its velocity at any point is given by v2=a+bx, where a,b≠0 are constants. The acceleration is
View Solution
