A particle starts from point A, moves along a straight line path with an accleration given by a=2(4−x) where x is distance from point A. The particle stops at point B for a moment. Find the distance AB (in m). (All values are in S.I. units)
The correct Answer is:8
To solve the problem, we need to find the distance AB where a particle starts from point A and stops at point B under the influence of a given acceleration. The acceleration is defined as:
a=2(4−x)
where \( x \) is the distance from point A.
1. Understand the acceleration equation:
The acceleration can be rewritten as:
\(
a = 8 - 2x
\)
2. Relate acceleration to velocity:
We know that acceleration \( a \) can be expressed as:
\(
a = \frac{dv}{dt} = v \frac{dv}{dx}
\)
Therefore, we can set up the equation:
\(
v \frac{dv}{dx} = 8 - 2x
\)
3. Separate variables and integrate:
Rearranging gives us:
\(
v dv = (8 - 2x) dx
\)
Now we integrate both sides. The left side integrates to:
\(
\int v \, dv = \frac{v^2}{2}
\)
The right side integrates to:
\(
\int (8 - 2x) \, dx = 8x - x^2
\)
Thus, we have:
\(
\frac{v^2}{2} = 8x - x^2 + C
\)
4. Apply initial conditions:
At point A, when \( x = 0 \), the particle starts from rest, so \( v = 0 \). Plugging in these values gives:
\(
0 = 8(0) - (0)^2 + C \implies C = 0
\)
Therefore, our equation simplifies to:
\(
\frac{v^2}{2} = 8x - x^2
\)
5. Determine when the particle stops:
The particle stops at point B, meaning \( v = 0 \). Setting \( v = 0 \) in our equation gives:
\(
0 = 8x - x^2
\)
Rearranging this, we factor out \( x \):
\(
x(8 - x) = 0
\)
This gives us two solutions: \( x = 0 \) (point A) or \( x = 8 \).
6. Conclusion:
The distance \( AB \) is therefore:
\(
AB = 8 \, \text{m}
\)
Final Answer:
The distance \( AB \) is \( 8 \, \text{m} \).
The acceleration can be rewritten as:
\(
a = 8 - 2x
\)
We know that acceleration \( a \) can be expressed as:
\(
a = \frac{dv}{dt} = v \frac{dv}{dx}
\)
Therefore, we can set up the equation:
\(
v \frac{dv}{dx} = 8 - 2x
\)
Rearranging gives us:
\(
v dv = (8 - 2x) dx
\)
Now we integrate both sides. The left side integrates to:
\(
\int v \, dv = \frac{v^2}{2}
\)
The right side integrates to:
\(
\int (8 - 2x) \, dx = 8x - x^2
\)
Thus, we have:
\(
\frac{v^2}{2} = 8x - x^2 + C
\)
At point A, when \( x = 0 \), the particle starts from rest, so \( v = 0 \). Plugging in these values gives:
\(
0 = 8(0) - (0)^2 + C \implies C = 0
\)
Therefore, our equation simplifies to:
\(
\frac{v^2}{2} = 8x - x^2
\)
The particle stops at point B, meaning \( v = 0 \). Setting \( v = 0 \) in our equation gives:
\(
0 = 8x - x^2
\)
Rearranging this, we factor out \( x \):
\(
x(8 - x) = 0
\)
This gives us two solutions: \( x = 0 \) (point A) or \( x = 8 \).
The distance \( AB \) is therefore:
\(
AB = 8 \, \text{m}
\)
The distance \( AB \) is \( 8 \, \text{m} \).
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS784videos
TEST PAPERS
- BOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS SEC - 220videos
TEST PAPERS
- BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems13videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS130videos
TEST SERIES
Similar Questions
The speed v of a particle moving along a straight line is given by a+bv2=x2 where x is its distance from the origin. The acceleration of the particle is
View SolutionA particle moving along a straight line with uniform acceleration has velocities 7m/s at A and 17m/s at C. B is the mid point of AC. Then :-
View Solution
Knowledge Check
- Question 1 - Select One
A particle starts from point A moves along a straight line path with an acceleration given by a = p - qx where p, q are connected and x is distance from point A . The particle stops at point B. The maximum velocity of the particle is
ApqBp√qCqpD√qp - Question 2 - Select One
A particle moves such that its accleration a is given by a=−bx, where x is the displacement from equilibrium position and b is a constant. The period of oscillation is
A√2π/bB2π/√bC2π/bD2√(π/b)
A particle starting from rest moves in a straight line with acceleration as shown in the a-t graph. Find the distance (in m) travelled by the particle in the first four seconds from start of its motion.
Q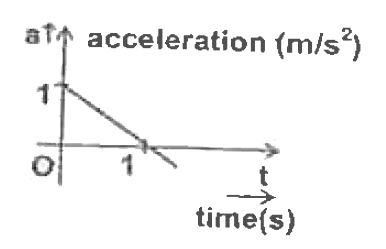 View Solution
View SolutionA particle starts moving in a straight line from rest with an acceleration (inm/s2) given by : a=12√x, where x is the distance travelled by the particle (in meters ) The velocity of the particle at the instant when its acceleration is 48m/s2 is .......m/s
View SolutionA particle, initially at rest, starts moving in a straight line with an acceleration a=6t+4m/s2. The distance covered by it in 3 s is
View SolutionA point P moves so that its distance from the line given by x=−3 is equal to its distance from the point (3, 0). Show that the locus of P is y2=12x.
View SolutionA particle starts to move in a straight line from a point with velocity 10 m s−1 and acceleration - 2.0 ms−2. Find the position and velocity of the particle at (i) t = 5 s, (ii) t' = 10 s.
View SolutionA particle moves along a straight line on y-axis. The distance of the particle from O varies with time and is given by : y=20t−t2. The distance travelled by the particle before it momentarily comes to rest is
View Solution

