Figure shows the graph of velocity versus displacement of a particle executing simple harmoic motion. Find the period of oscillation of the particle.

Text Solution

Verified by Experts

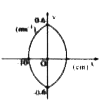
$x_{max} = A = 10 c m$ and
$v_{max} = ω A = 0.6 m s^{- 1}$
$∴ ω = \frac{v_{max}}{x_{max}} = \frac{6 \times 10^{- 1}}{10 \times 10^{- 2}} = 6 r a d s^{- 1}$
$∴ T = \frac{2 π}{ω} = \frac{2 π}{6} = \frac{π}{3}$ sec

Updated on:21/07/2023

The velocity of a particle executing simple harmonic motion is
A $ω^{2} \sqrt{A^{2} + x^{2}}$
B $ω \sqrt{A^{2} - x^{2}}$
C $ω \sqrt{A^{2} + x^{2}}$
D $ω^{2} \sqrt{A^{2} - x^{2}}$
The displacement of a particle executing simple harmonic motion is given by $y = 4 sin (2 t + ϕ)$ . The period of oscillation is
A $2 / π$
B $π / 2$
C $π$
D $2 π$
If a particle is executing simple harmonic motion, then acceleration of particle
Ais uniform
Bvaries linearly with time
Cis non uniform
DBoth (2) & (3)