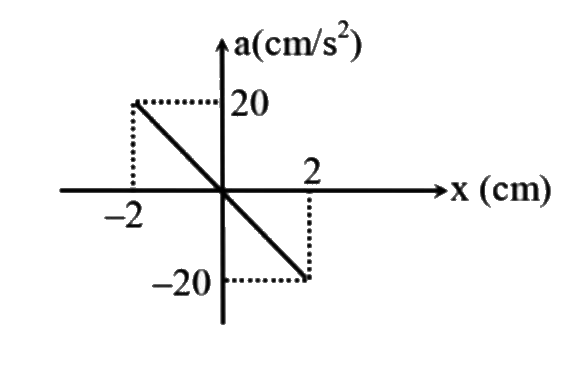
Figure. Shows the variation of force acting on a particle of mass 400 g executing simple harmonic motion. The frequency of oscillation of the particle is

A

$4 s^{- 1}$

B

$(\frac{5}{2 π}) s^{- 1}$

C

$(\frac{1}{8 π}) s^{- 1}$

D

$(\frac{1}{2 π}) s^{- 1}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

The slope of the length is
$\frac{F}{x} = - \frac{0.5}{5} = - 0.1 \frac{N}{c m} = - 10 \frac{N}{m}$
But $F = - m ω^{2} x$ or $\frac{F}{x} = - m ω^{2}$
so, $- m ω^{2} = - 10$ or $m ω^{2} = 10$
or $ω^{2} = \frac{10}{m}$
$ω^{2} = \frac{10}{4 \times 10^{- 1}} \Rightarrow ω = \frac{10}{2} = 5$
$f = \frac{ω}{2 π} = \frac{\frac{5}{2 π}}{s}$

|

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
While a particle executes linear simple harmonic motion
Aits linear velocity and acceleration pass through their maximum and minimum values once in each oscillation.
BIts linear velocity and acceleration pass through their maximum and minimum values twice in each oscillation.
Cits linear velocity and acceleration pass through their maximum and minimum values four times in each oscillation.
Dits linear velocity and acceleration always attain their peak values simlataneaously.
Question 2 - Select One
The velocity of a particle executing simple harmonic motion is
A $ω^{2} \sqrt{A^{2} + x^{2}}$
B $ω \sqrt{A^{2} - x^{2}}$
C $ω \sqrt{A^{2} + x^{2}}$
D $ω^{2} \sqrt{A^{2} - x^{2}}$
Question 3 - Select One
In simple harmonic motion,the particle is
Aalways acceleration
Balways retarded
Calternately acceleration and retarded
Dneither acceleration nor retarded

CENGAGE PHYSICS-LINEAR AND ANGULAR SIMPLE HARMONIC MOTION-Single Correct

Home
Ask Doubt
Profile