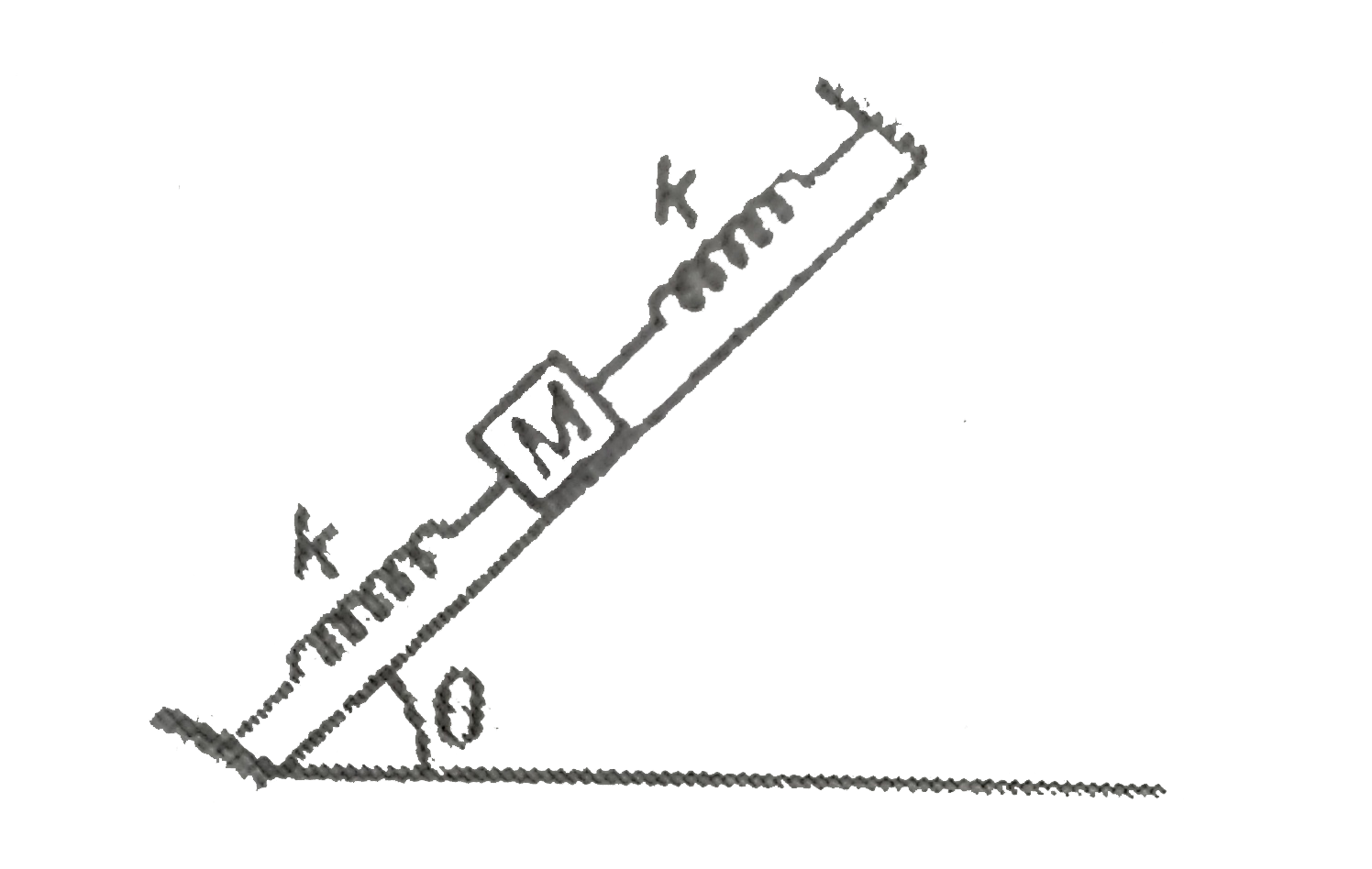
On a smooth inclined plane a body of mass M is attached between two springs. The other ends of the springs ar fixed to firm supports. If each spring has a force constant k, find the period of oscillation of the body.
keff=2K
∴T=2π√M2k
period (or keff) is independent of θ
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE I184videos
OSCILLATIONS
- BOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE II175videos
OSCILLATIONS
- BOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE-349videos
OSCILLATIONS
- BOOK - AAKASH SERIESCHAPTER - OSCILLATIONEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS12videos
OSCILLATION
- BOOK - AAKASH SERIESCHAPTER - PHYSICAL WORLDEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS5videos
PHYSICAL WORLD
Similar Questions
On a smooth inclined plane a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has a force constant k, the period of oscilation of the body is (assuming the spring as massless)
View Solution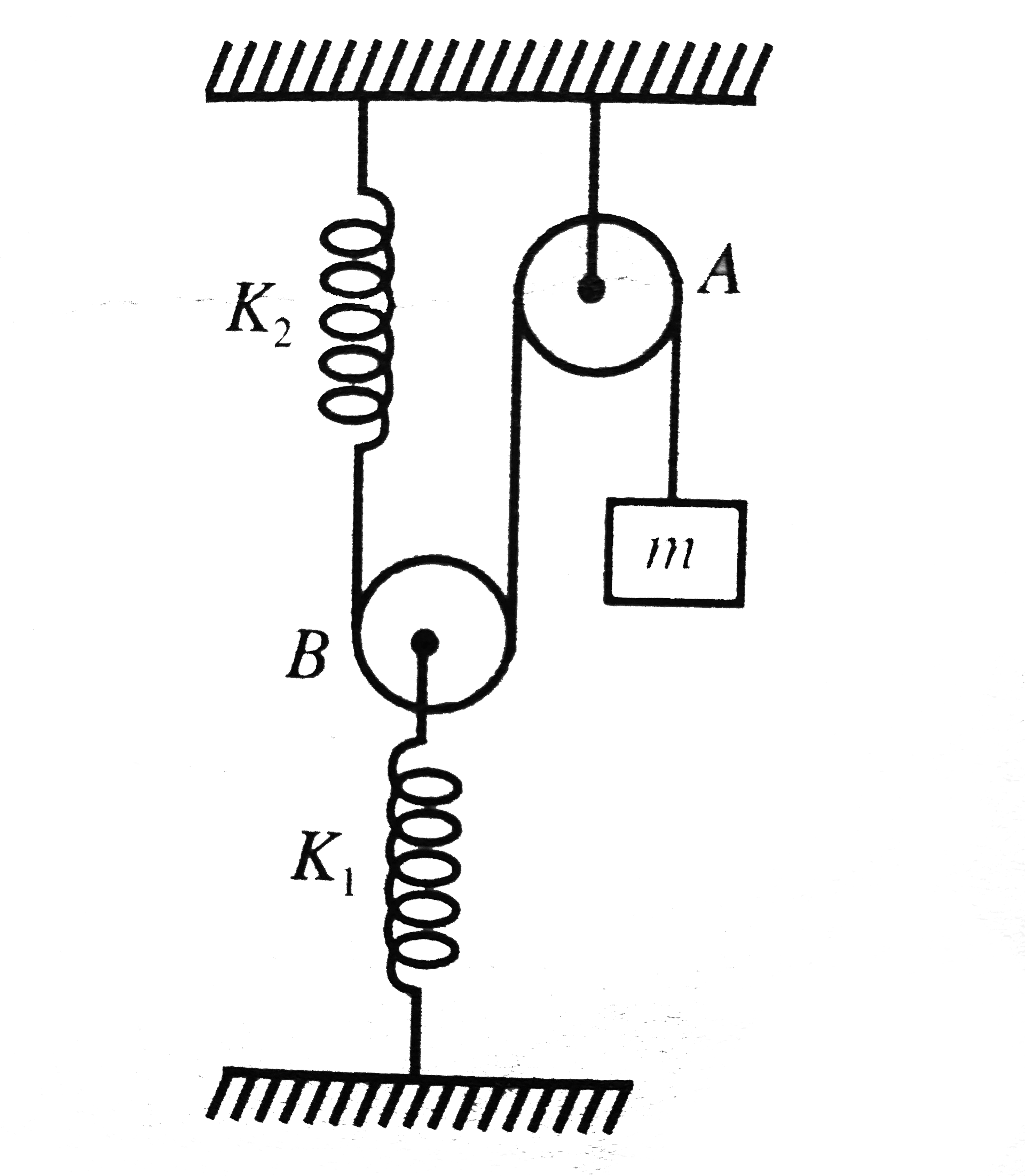
A block of mass m is tied to one end of a spring which passes over a smooth fixed pulley A and under a light smooth movable pulley B. The other end of the string is attached to the lower end of a spring of spring constant K2. Find the period of small oscillation of mass m about its equilibrium position (in second). (Take m=π2kg,K2k=4K1,K1=17Nm.)View Solution
Knowledge Check
- Question 1 - Select One
On a smooth inclined plane a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has a force constant k, the period of oscilation of the body is (assuming the spring as massless)
A2π√M2kB2π√2Mk)C2π√Msinθ2kD2π√2Msinθk) - Question 2 - Select One
On a smooth inclined plane a body of mass M is attached between two springs. The other ends of the spring are fixed to ffirm supports. If each spring has a force constant k, the period of oscillation of the body is: (assuming the spring as massless)
A2π√M2KB2π√2MKC2π√MSinθKD2π√2MSinθK - Question 3 - Select One
On a smooth inclined plane, a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has force constant K , the period of oscillation of the body (assuming the springs as massless) is
A2π(m2K)1/2B2π(2MK)1/2C2πMgsinθ2KD2π(2MgK)1/2
-
A block of mass m is tied to one end of a spring which passes over a smooth fixed pulley A and under a light smooth movable pulley B. The other end of the string is attached to the lower end of a spring of spring constant K2. Find the period of small oscillation of mass m about its equilibrium position (in second). (Take m=π2kg,K2k=4K1,K1=17Nm.)View Solution In the adjacent figure, if the incline plane is smooth and the springs are identical then the period of oscillation of this body is
View SolutionA light pulley is suspended at the lower end of a spring of constant k1, as shown in figure. An inextensible string passes over the pulley. At one end of string a mass m is suspended, the other end of the string is attached to another spring of constant k2. The other ends of both the springs are attached to rigid supports, as shown. Neglecting masses of springs and any friction, find the time period of small oscillations of mass m about equilibrium position.
View SolutionOn a smooth inclined plane, a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has force constant K , the period of oscillation of the body (assuming the springs as massless) is
View SolutionIn the adjacent figure, if the incline plane is smooth and the springs are identical then the period of oscillation of this body is
View Solution