A mass m=8kg is attached to a spring as shown in figure and held in position so that the spring remains unstretched. The spring constant is 200 N/m. The mass m is then released and begins to undergo small oscillations. Find the maximum velocity of the mass (g=10m/s2)
Mean position will be at k,x=mg or
x=mgk=8×10200=25=0.4m
This is also the amplitude of oscillation
i.e. A=0.4m
Now vmax=Aω=A√km=(0.4)√2008=2m/s

Topper's Solved these Questions
- OSCILLATIONSBook:AAKASH SERIESChapter:OSCILLATIONSExercise:EXERCISE I
Explore 184 Videos
- OSCILLATIONSBook:AAKASH SERIESChapter:OSCILLATIONSExercise:EXERCISE II
Explore 175 Videos
- OSCILLATIONSBook:AAKASH SERIESChapter:OSCILLATIONSExercise:EXERCISE-3
Explore 49 Videos
- OSCILLATIONBook:AAKASH SERIESChapter:OSCILLATIONExercise:QUESTIONS FOR DESCRIPTIVE ANSWERS
Explore 12 Videos
- PHYSICAL WORLDBook:AAKASH SERIESChapter:PHYSICAL WORLDExercise:VERY SHORT ANSWER TYPE QUESTIONS
Explore 5 Videos
Similar Questions
A mass m = 8kg is attached to a spring as shown in figure and held in positioin so that the spring remains unstretched. The spring constant is 200 N/m. The mass m is then released and begins to undergo small oscillations. The maximum velocity of the mass will be (g=10m/s2)
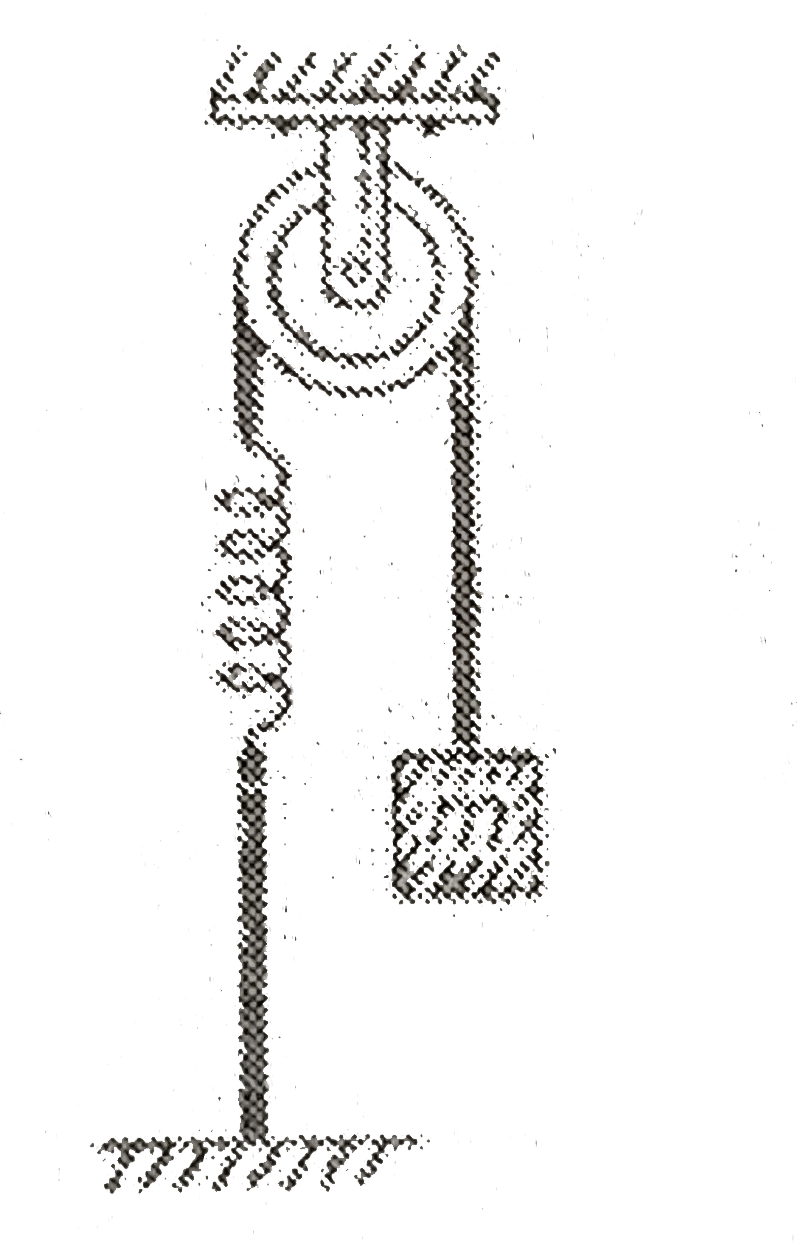
View SolutionA mass M=5 kg is attached to a string as shown in the figure and held in position so that the spring remains unstretched. The spring constant is 200Nm−1 . The mass M is then released and begins to undergo small oscillations. The amplitude of oscillation is
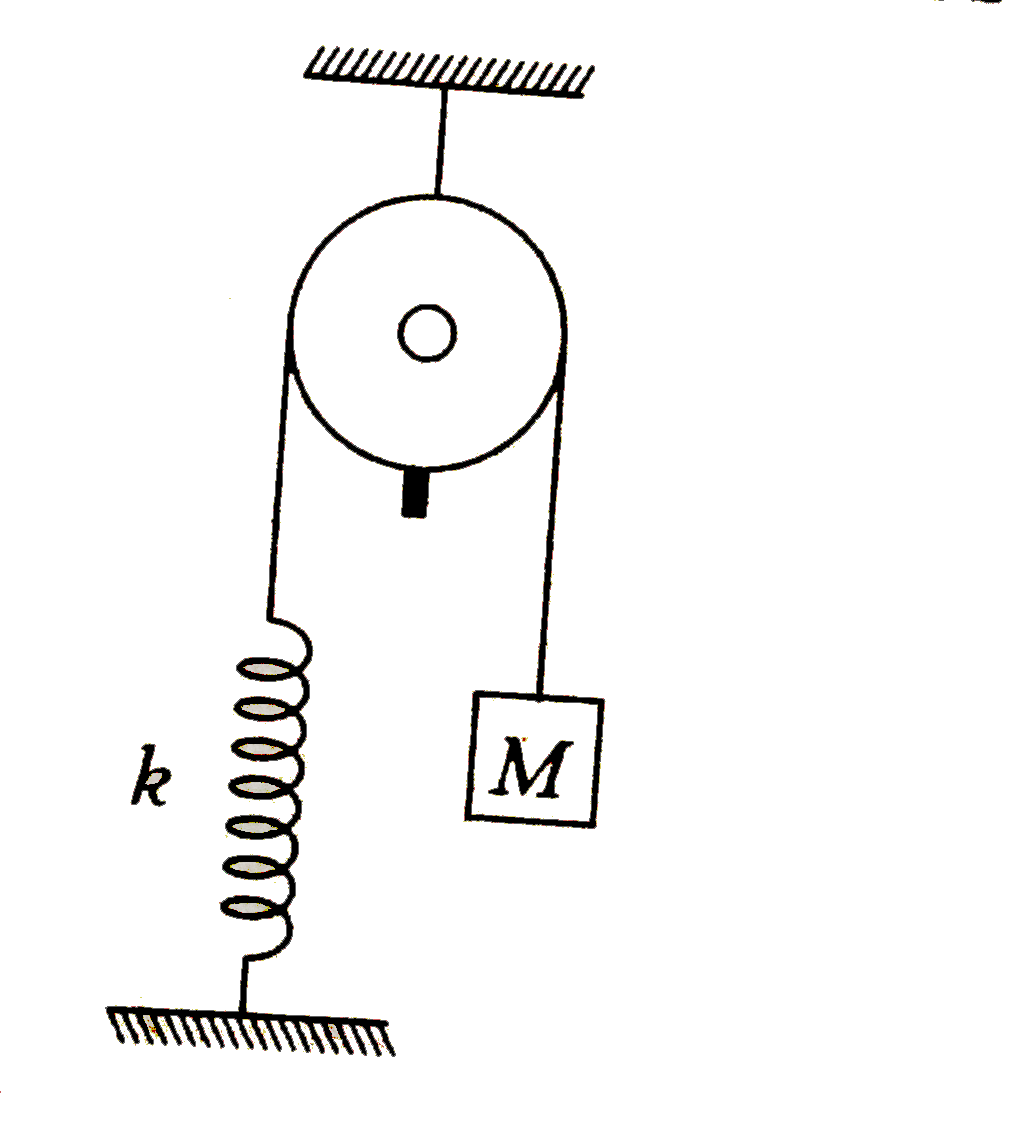
View Solution
Knowledge Check
A mass m=8kg is attached to a spring as shown in figure and held in position so that the spring remains unstretched. The spring constant is 200N/m. The mass m is then released and begins to undergo small oscillations. The maximum velocity of the mass will be (g=10m/s2)
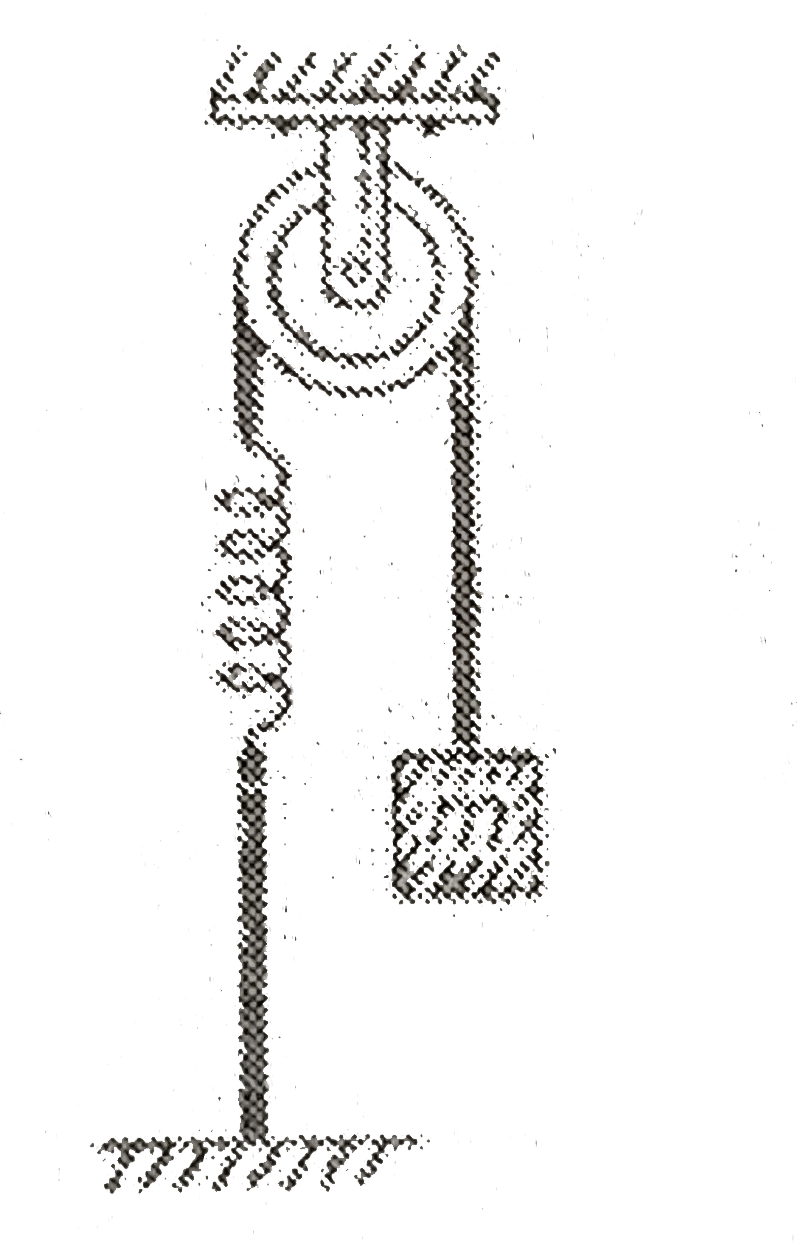 A1 m/sB2 m/sC4 m/sD5 m/s
A1 m/sB2 m/sC4 m/sD5 m/sA mass M=5 kg is attached to a string as shown in the figure and held in position so that the spring remains unstretched. The spring constant is 200Nm−1 . The mass M is then released and begins to undergo small oscillations. The amplitude of oscillation is
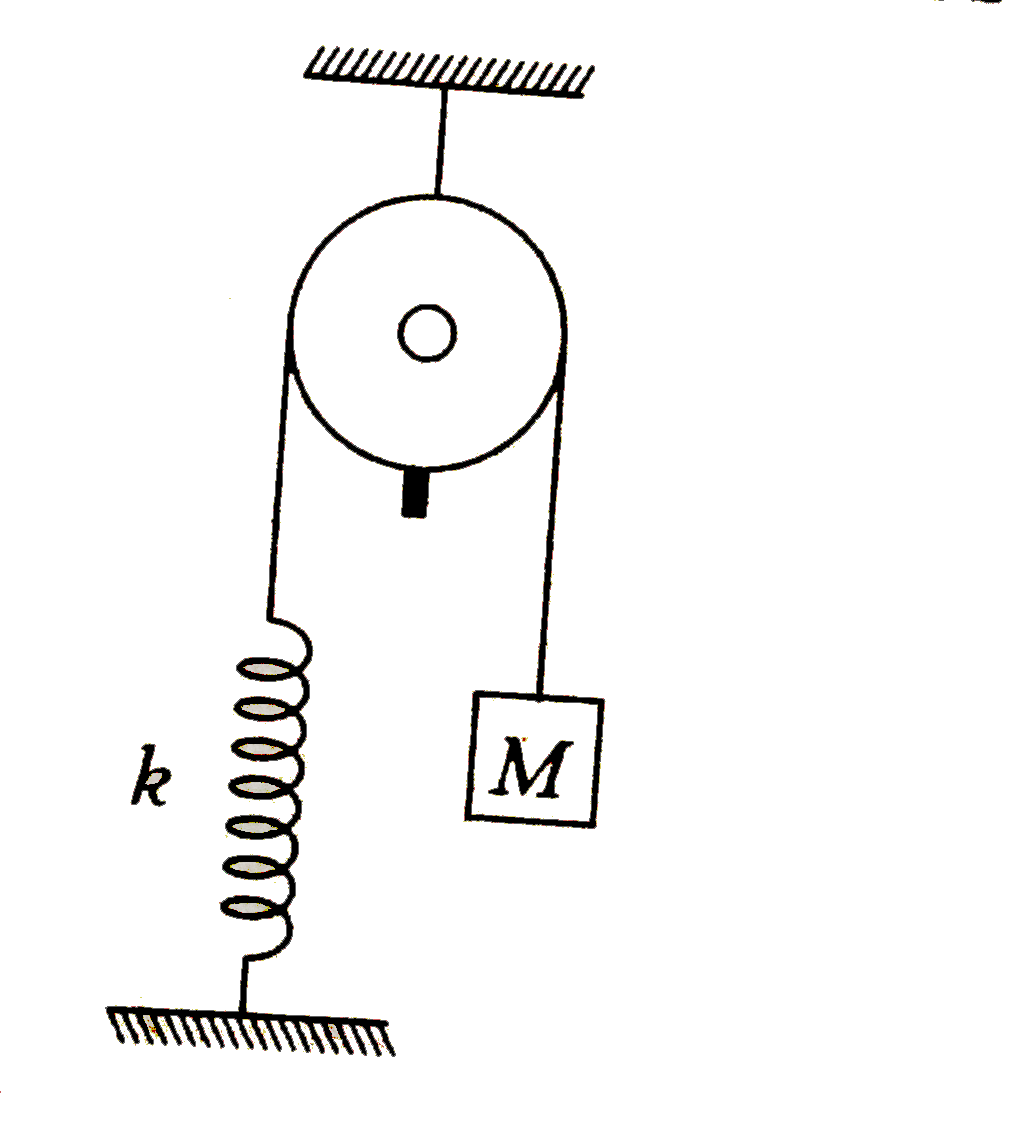 A0.5 mB0.25 mC0.2 mD0.1 m
A0.5 mB0.25 mC0.2 mD0.1 mThe arranghement shown in the figure below consits of a block of mass 0.1 kg attached to a spring of force cosntant 2×10−3N/M with the help of a pulley so that the spring remians unstretched.On releasing the block , it starts oscillating with a small amplitude . The maximum velocity of block during this motion is close to
A72m/sB71m/sC70m/sD69m/s
A mass m=8kg is attached to a spring passing over a pulled whose other end is fixed to ground and held in position so that the spring remains unstretched. The spring constant is 200N/m. The mass m is then released and begins to undergo small oscillations. Find maximum velocity of mass
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionThe time period of an oscillating spring of mass 630 g and spring constant 100 N/m with a load of 1 kg is
View SolutionTwo masses m1 and m2 are attached to a spring balance S as shown in figure. m1>m2 then the reading of spring balance will be .
 .
.
View Solution
