Frequency of a particle executing SHM is 10 Hz. The particle is suspended from a vertical spring. At the highest point of its oscillation the spring is unstretched. Find the maximum speed of the particle:
$(g = 10 m / s^{2})$

Text Solution

Verified by Experts

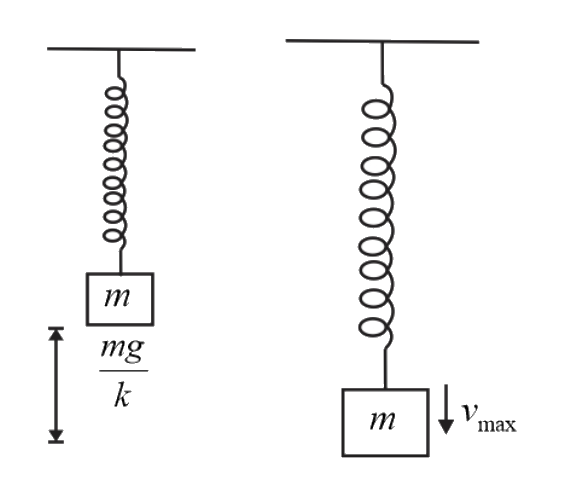
Mean position of the particle is $\frac{m g}{k}$ distance below unstretched position of spring. Therefore, amplitude of oscillation is
$A = \frac{m g}{k} ω = \sqrt{\frac{k}{m}} = 2 π f = 20 π$
$∴ \frac{m}{k} = \frac{1}{400 π^{2}}$
Therefore the maximum speed of particle will be
$v_{max} = A ω = (\frac{g}{400 π^{2}}) (20 π) = \frac{1}{2 π} m / s$

|

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Frequency of a particle executing SHM is 10 Hz. The particle is suspended from a vertical spring. At the highest point of its oscillation the spring is unstretched. Maximum speed of the particle is (g=10m/ $s^{2}$
A $2 π m / s$
B $π m / s$
C $\frac{1}{π} m / s$
D $\frac{1}{2 π} m / s$
Question 2 - Select One
Frequency of a particle executing SHM is 10 Hz. The particle is suspended from a vertical spring. At the highest point of its oscillation the spring is unstretched. Maximum speed of the particle is $(g = 10 \frac{m}{s})$
A $2 π \frac{m}{s}$
B $π \frac{m}{s}$
C $\frac{1}{π} \frac{m}{s}$
D $\frac{1}{2 π} / \frac{m}{s}$
Question 3 - Select One
A particle suspended from a vertical spring oscillates 8 times per second. At the highest point of oscillation the spring becomes unstretched. The maximum speed of the block will be
A10 cm/s
B20 cm/s
C30 cm/s
D40 cm/s

AAKASH SERIES-OSCILLATIONS-PROBLEM

Home
Ask Doubt
Profile