The angular velocities of three bodies in SHM are w1,w2,w3 with their respective amplitudes as A1A2A3. If all three bodies have same mass and velocity then
A1w1=A2w2=A3w3
A1w21=A2w22=A3w23
A21w1=A22w2=A23w3
A21w11=A22w22=A23w33
The correct Answer is:A
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - Practice exercise
140 Videos
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE -I Equation of S.H.M
51 Videos
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE I
184 Videos
- OSCILLATIONBOOK - AAKASH SERIESCHAPTER - OSCILLATIONEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
12 Videos
- PHYSICAL WORLDBOOK - AAKASH SERIESCHAPTER - PHYSICAL WORLDEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
5 Videos
Similar Questions
Two waves of nearly same amplitude , same frequency travelling with same velocity are superimposing to give phenomenon of interference . If a1 and a2 be their respectively amplitudes , ω be the frequency for both , v be the velocity for both and Δϕ is the phase difference between the two waves then ,
View SolutionIf a1,a2,a3 are the last three digits of 17256 respectively then the value of a2−a1−a3 is equal
View Solution
Knowledge Check
The angular velocities of three bodies in SHM are ω1,ω2,ω3 with their respective amplitudes as A1,A2,A3. If all three bodies have same mass and maximum velocity then
AA1ω1=A2ω2=A3ω3BA1ω21=A2ω22=A3ω23CA21ω1=A22ω2=A22ω2DA21ω21=A22ω22=A23ω23If last three digits of the expression 17256 are
A1,A2 & A3 respectively then the value of expression 2A2+A3−44A1 equalsA0B−4C5D−7Two waves of nearly same amplitude , same frequency travelling with same velocity are superimposing to give phenomenon of interference . If a1 and a2 be their respectively amplitudes , ω be the frequency for both , v be the velocity for both and Δϕ is the phase difference between the two waves then ,
Athe resultant intensity varies periodically with time and distance.Bthe resulting intensity with IminImax=a1−a2(a1+a2)2 is obtained.Cboth the waves must have been travelling in the same direction and must be coherent.DIR=I1+I2+2√I1I2cos(Δϕ), where constructive interference is obtained for path difference that are odd multiple of 1/2λ and destructive interference is obtained for path difference that are even multiple of 1/2λ.
find all the possible triplets (a1,a2,a3) such that a1+a2cos(2x)+a3sin2(x)=0 for all real x.
View Solutionfind all the possible triplets (a1,a2,a3) such that a1+a2cos(2x)+a3sin2(x)=0 for all real x.
View SolutionThe number of all three element subsets of the set {a1,a2,a3......an} which contain a3 , is
View SolutionThe number of all three element subsets of the set {a1,a2,a3......an} which contain a3 , is
View SolutionIn the adjacent figure, all the pulleys are frictioniess and massless, all the stringes are also massless. The relation between a1,a2 and a3 is (where a1,a2 and a3 are the acceleration of masses m1,m2 and m3 respectively in the direction as shown in the figure)
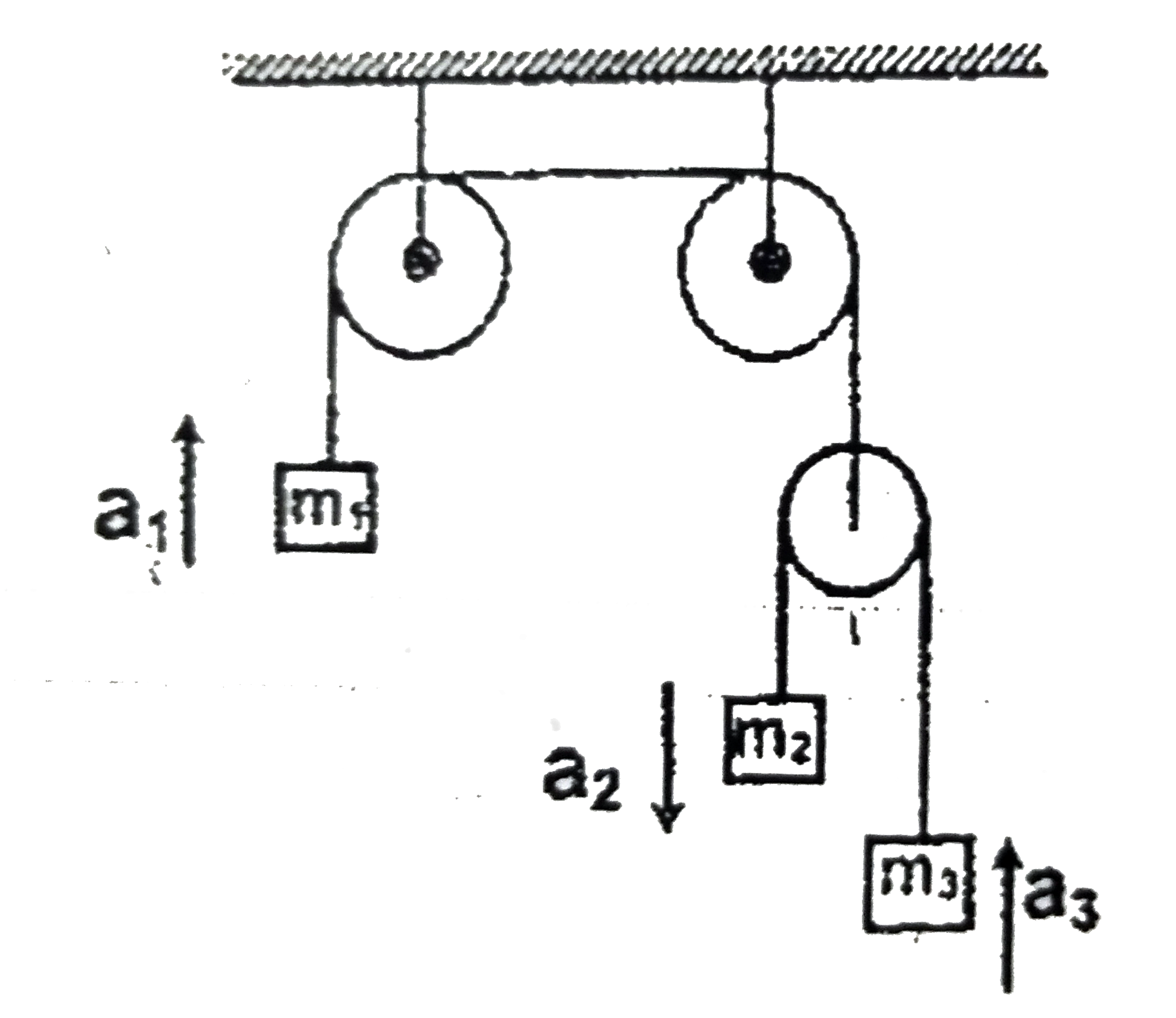
View Solution
