The velocity of a particle under going SHM at the mean positon is 2ms−1. Find the velocity of the particle at the point where the displacement form the mean position is equal to half the amplitude
1.234ms−1
1.732ms−1
2.732ms−1
1.414ms−1
The correct Answer is:B
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - Practice exercise
140 Videos
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE -I Equation of S.H.M
51 Videos
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE I
184 Videos
- OSCILLATIONBOOK - AAKASH SERIESCHAPTER - OSCILLATIONEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
12 Videos
- PHYSICAL WORLDBOOK - AAKASH SERIESCHAPTER - PHYSICAL WORLDEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
5 Videos
Similar Questions
A graph between velocity and displacement of a particle performing SHM is shown. Find the acceleration when the particle is at half of maximum displacement from mean position.
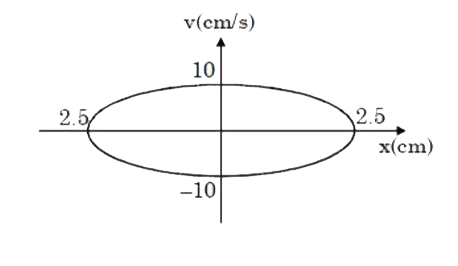
View SolutionA particle is performing SHM. At what distance from mean position, the velocity of the particle becomes half of the maximum velocity ?
View Solution
Knowledge Check
The velocity of a particle performing S.H.M. at mean position is
AmaximumBhalf of the maximumCminimumDzeroThe velocity of a particle in simple harmonic motion at displacement y from mean position is
Aω√(a2+y2)Bω√(a2−y2)CwyDω2√(a2+y2)The velocity of a particle in simple harmonic motion at displacement y from mean position is
Aω√a2+y2Bω√a2−y2CωyDω2√a2−y2
A particle executes a simple harmonic motion of time period T. Find the time taken by the particle to go directly from its mean position to half the amplitude.
View SolutionA particle executes a simple harmonic motion of time period T. Find the time taken by the particle to go directly from its mean position to half the amplitude.
View SolutionA particle executing SHM passes through the mean position with a velocity of 4ms−1. The velocity of the particle at a point where the displacement is half of the amplitude is
View SolutionThe velocity of particle undergoing SHM is v at the mean position. If only amplitude is doubled, the velocity at mean position
View SolutionVelocity at mean position of a particle executing S.H.M. is v , they velocity of the particle at a distance equal to half of the amplitude
View Solution
