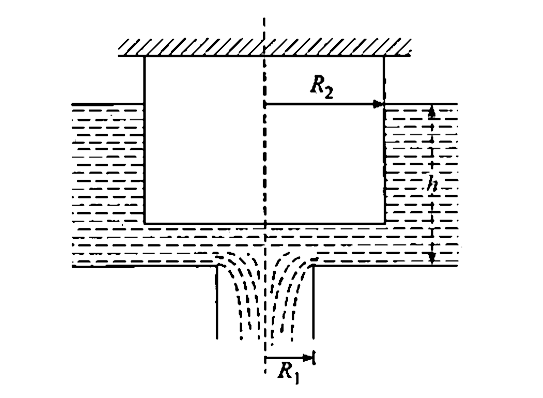
The horizontal bottom of a wide vessel with an ideal fluid has a round orifice of radius R1 over which a round closed cylinder is mounted, whose radius R(2)>R1 The clearance between the cylinder and the bottom of the vessel is very small, the fluid density is ρ. Find the static pressure of the fluid in the clearance as a function of the distance from the axis of the orifice and the cylinder), if the height of the fluid is

Pa+ρgh[1−R21r2]
Topper's Solved these Questions
- FLUID MECHANICSBOOK - AAKASH SERIESCHAPTER - FLUID MECHANICSEXERCISE - Numerical Exercise (LEVEL-2)
18 Videos
- EXPANSION OF SOLIDS BOOK - AAKASH SERIESCHAPTER - EXPANSION OF SOLIDS EXERCISE - Questions for Descriptive Answers
5 Videos
- FRICTION BOOK - AAKASH SERIESCHAPTER - FRICTION EXERCISE - ADDITIONAL PRACTICE EXERCISE PRACTICE SHEET (ADVANCED) (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
1 Videos
Similar Questions
The horizontal bottom of wide vessel with an ideal fluid has a round orifice of radius R1 over which a round closed cylinder is mounted, whose radius R2>R1 (figure). The clearance between the cylinder and the bottom of the vessel is very small, the fluid density is ρ. Find the static pressure of the fluid in the clearance as a function of the distance r from the axis of the orifice (and the cylinder), if the height of the fluid is equal to h.

View SolutionThe horizontal bottom of a wide vessel with an ideal fluid has a round orifice of radius R1 over which a round closed cylinder is mounted, whose radius R2>R1figure. The clearance between the cylinder and the bottom of the vessel is very small, the fluid density is ρ. find the static pressure of the fluid in the clearance as a function of the distance r from the axis of the orifice (and the cylinder) , if the height of the fluid is equal to h.
View Solution
Knowledge Check
A tube of length 1 and radius R carries a steady flow of fluid whose density is ρ and viscosity η. The velocity v of flow is given by v=v0(1−r2/R2) Where r is the distance of flowing fluid from the axis.
A4πηlV0B2πηlV0CπηlV0D23πηlV0A hemispherical portion of a radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at a depth of h below the liquid surface. THe force on the bottom of the cylinder by the liquid is
AM gBMg−Vρ gCMg+ΠR2hgρDρg(V+ΠR2h)A hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass M. It is suspended by a string in a liquid of density ρ where it stays vertical. The upper surface of the cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder by the liquid is
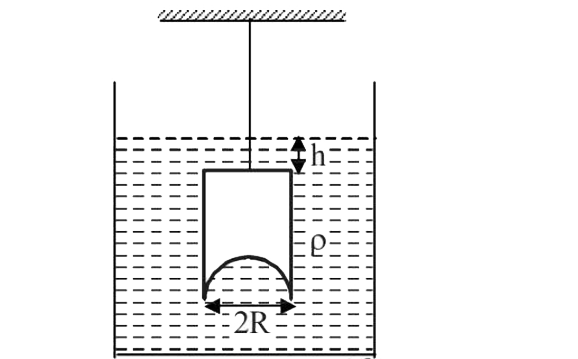 A(a) MgB(b) Mg−VρgC(c) Mg+πR2hρgD(d) ρg(V+πR2h)
A(a) MgB(b) Mg−VρgC(c) Mg+πR2hρgD(d) ρg(V+πR2h)
A long cylinder of radius R1 is displaced along its axis with a constant velocity v0 inside a stationary co-axial cylinder of radius R2. The space between the cylinders is filled with viscous liquid. Find the velocity of the liquid as a function of the distance r from the axis of the cylinders. The flow is laminar.
View SolutionWater flows out of a wide vessel through a small orifice. Express the flow velocity as a function of the height of the column of liquid.
View SolutionA conical portion of radius R and height H is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at depth h below the liquid surface . The force on the bottom of the cylinder by the liquid is
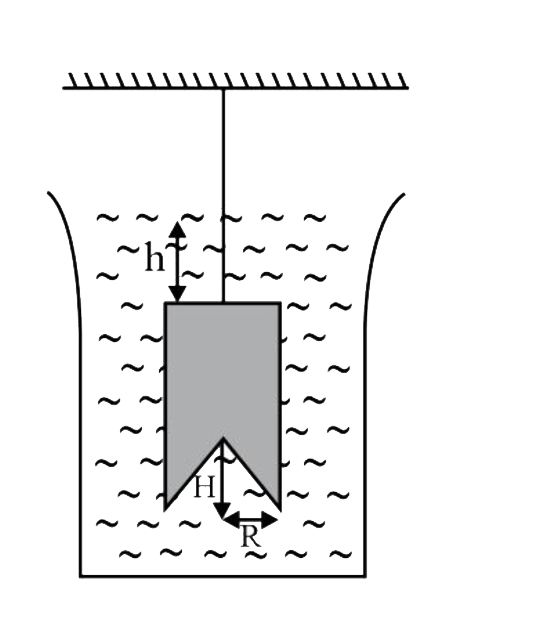
View SolutionA conical portion of radius R and height H is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at depth h below the liquid surface . The force on the bottom of the cylinder by the liquid is

View SolutionA hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass M. It is suspended by a string in a liquid of density ρ where it stays vertical. The upper surface of the cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder by the liquid is

View Solution
