A small tube is bent in the form of a circle whose plane is vertical. Equal quantities by volume of two fluids of densities ρ and σ fill half the tube. Find the angle ϕ that the radius passing through the common surface makes with the vertical.
tanϕ=ρ−σρ+σ(ρ>σ)
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - FLUID MECHANICSEXERCISE - Numerical Exercise (LEVEL-2)18videos
FLUID MECHANICS
- BOOK - AAKASH SERIESCHAPTER - EXPANSION OF SOLIDS EXERCISE - Questions for Descriptive Answers5videos
EXPANSION OF SOLIDS
- BOOK - AAKASH SERIESCHAPTER - FRICTION EXERCISE - ADDITIONAL PRACTICE EXERCISE PRACTICE SHEET (ADVANCED) (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)1videos
FRICTION
Similar Questions
A small uniform tube is bent into a circle of radius r whose plane is vertical. Equal volumes of two fluids whose densities areρ and σ(ρ>σ) fill half the circle. Find the angle that the radius passing through the interface makes with the vertical.
View SolutionA uniform long tube is bent into a circle of radius R and it lies in vertical plane. Two liquids of same volume but densities ρ and δ fill half the tube. The angle θ is
View Solution
Knowledge Check
- Question 1 - Select One
A small uniform tube is bent into a circle of radius r whose plane is vertical. Equal volumes of two fluids whose densities areρ and σ(ρ>σ) fill half the circle. Find the angle that the radius passing through the interface makes with the vertical.
Atan−1(ρ+σρ−σ)Btan−1(ρ−σρ−σ)Ctan−1(ρ+σρ+σ)Dtan−1(ρ−σρ+σ) - Question 2 - Select One
A uniform long tube is bent into a circle of radius R and it lies in vertical plane. Two liquids of same volume but densities ρ and δ fill half the tube. The angle θ is
Atan−1(ρ−δρ+δ)Btan−1(ρδ)Ctan−1(δρ)Dtan−1(ρ+δρ−δ) - Question 3 - Select One
A thin uniform tube is bent into a circle of radius r in the vertical plane. Equal volumes of two immiscible liquids, whose densities are ρ1 and ρ2(ρ1>ρ2) fill half the circle. The angle θ between the radius vector passing though the common interface and the vertical is :
Aθ=tan−1'π2(ρ2ρ1)Bθ=tan−1'π(ρ1ρ2)Cθ=tan−1'π2(ρ1+ρ2ρ1−ρ2)Dθ=tan−1'[π2(ρ1+ρ2ρ1−ρ2)]
A thin uniform circular tube is kept in a vertical plane. Equal volume of two immiscible liquids whose densites are ρ1 and ρ2 fill half of the tube as shown. In equilibrium the radius passing through the interface makes an angle of 30∘ with vertical. The ratio of densities (ρ1/ρ2) is equal to
View SolutionTwo non-viscous, incompressible and immiscible liquids of densities p and 1.5p are poured into the two limbs of a circular tube of radius R and small cross section kept fixed in a vertical plane as shown in the figure. Each liquid occupies one fourth the circumference of the tube.
(i)Find the angle theta that the radius to the interface makes with the vertical in equilibrium position. _________
(ii) If the whole liquid column is given a small displacement from its equilibrium position, show that the resulting oscillations are simple harmonic. Find the time period of these oscillations. ____________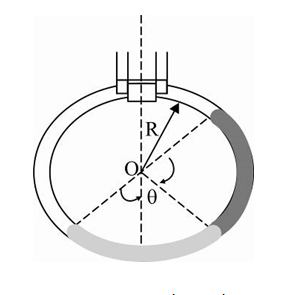
View SolutionTwo non - viscous, incompressible and immiscible liquids of densities (rho) and (1.5 rho) are poured into the two limbs of a circular tube of radius ( R) and small cross section kept fixed in a vertical plane as shown in fig. Each liquid occupies one fourth the cirumference of the tube.
Find the angle (theta) that the radius to the interface makes with the verticles in equilibrium position.View SolutionTwo non-viscous, incomoressible and immiscible liquids of densities ρ and 1.5ρ are poured into the two limbs of a circules tube of radius R and small cross-section kept fixed in a vertical plane as shown in fig. Each liquid occupies one-fourth the cirumference of the tube.
(a) Find the angle θ the radius to the interface makes with the vertical in equilibrium position.
(b) If the whole liquid column is given a small displacement from its equilibrium position, show that the resulting oscillations alre simple harmonic. Find the time period of these oscillations.View SolutionA thin uniform circular tube is kept in a vertical plane. Equal volume of two immiscible liquids whose densites are ρ1 and ρ2 fill half of the tube as shown. In equilibrium the radius passing through the interface makes an angle of 30∘ with vertical. The ratio of densities (ρ1/ρ2) is equal to
View Solution