Light of wavelength $λ = 500 n m$ falls on two narrow slits placed a distance $d = 50 \times 10^{- 4} c m$ apart, at an angle $ϕ = 30^{\circ}$ relative to the slits as shown in figure. On the lower slit, a transparent slab of thickness 0.1 mm and refractive index 3/2 is placed. The interference pattern is observed on a screen at a distance D = 2m from the slits. Then calculate
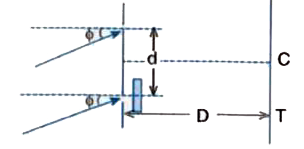
$Light of wavelength lamda = 500nm falls on two narrow slits placed a distance d = 50 xx 10^(-4) cm apart, at an angle phi =30^@ relative to the slits as shown in figure. On the lower slit, a transparent slab of thickness 0.1 mm and refractive index 3/2 is placed. The interference pattern is observed on a screen at a distance D = 2m from the slits. Then calculate (a) position of the central maxima? (b) the order of minima closest to centre C of screen ? (c) How many fringes will pass over C, if we remove the transparent slab from the lower slit?$
(a) position of the central maxima? (b) the order of minima closest to centre C of screen ? (c) How many fringes will pass over C, if we remove the transparent slab from the lower slit?

Text Solution

Verified by Experts

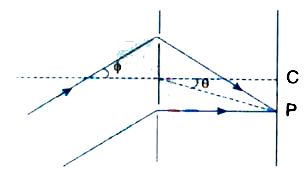
(a) Path difference,
$Δ x = d sin ϕ + d sin θ - (μ - 1) t$
For central maxima,
$Δ x = 0 ∴ sin θ = \frac{(μ - 1) t}{d} - sin ϕ$
$sin θ = \frac{(3 / 2 - 1) (0.1)}{50 \times 10^{- 3}} - {sin 30}^{\circ}, sin θ = \frac{1}{2}$
$∴ θ = 30^{\circ}$
(b) At $C, θ = 0^{\circ}$ , therefore
$Δ x = d sin θ - (μ - 1) t = (50 \times 10^{- 3}) (\frac{1}{2}) - (3 / 2 - 1) (0.1)$
$= 0.025 - 0.05 = - 0.025 m m$
Substituting $Δ x = n λ,$ we get
$n = \frac{Δ x}{λ} = \frac{- 0.025}{500 \times 10^{- 6}} = - 50$
Hence at C, there will be 50th maxima. Therefore, closest to C, order of minima is -49 (c) Number of fringes shifted upwards on removing the slab
$= \frac{(μ - 1) t}{λ} = \frac{(\frac{3}{2} - 1) 0.1}{500 \times 10^{- 6}} = 100$

Updated on:21/07/2023

In Young's double slit experiment the two slits are d distance apart. Interference pattern is observed on a screen at a distance D from the slits. A dark fringe is observed on the screen directly opposite to one of the slits. The wavelength of light is
A $\frac{D^{2}}{2 d}$
B $\frac{d^{2}}{2 D}$
C $\frac{D^{2}}{d}$
D $\frac{d^{2}}{D}$
A long narrow horizontal slit lies $1 m m$ above a plane mirror. The interference pattern produced by the slit and its and its image is viewed on a screen $\sum$ distance $1 m$ from the slit. The wavelength of light is $600 n m$ . Then the distance of the first maxima above the mirror is equal to $(d < < D)$ :

A $0.30 m m$
B $0.15 m m$
C $60 m m$
D $7.5 m m$