A thin film is illuminated by wavelength 600 nm in free space at nearly normal incidence. Calculate the minimum thickness of a thin film (μ = 3/2 ) that results in constructive interference in the reflected light.
For constructive interference 2μt=(2n+1)λ2
n=0,1,2, ..... For n=0, 2 (32)t=6002,t=100nm
Topper's Solved these Questions
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - PROBLEMS (LEVEL - I)
18 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - PROBLEMS (LEVEL - II)
20 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED ) Straight Objective Type Questions)
12 Videos
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)
81 Videos
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)
15 Videos
Similar Questions
A ray of light is incident at an angle of 45∘ (ralative to the normal) on a thin film of a liquid with an index of refraction of √2. Assuming that the medium of both sides of the film is air, find the minimum thickness of the film required for constructive interference in the reflected light for sodium light of wavelenght 600 nm.
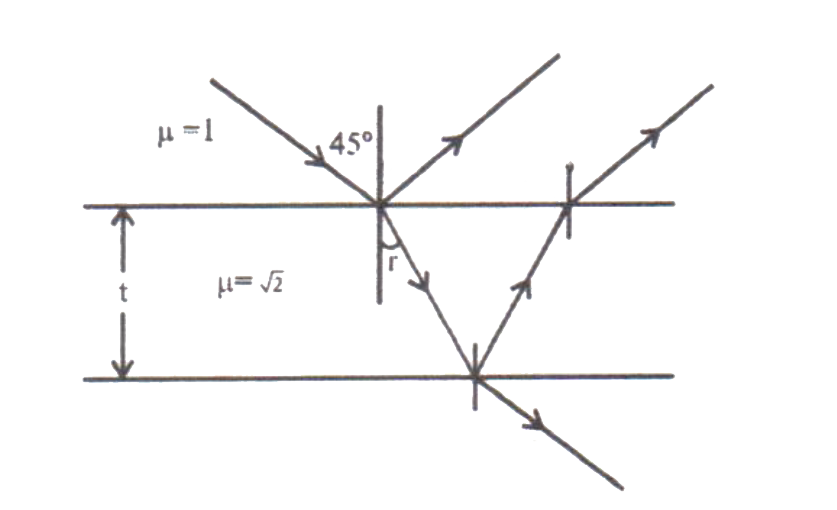
View SolutionWhite light is incident normally on a thin glass plate of refractive index 1.5. Calculate the minimum thickness of the film for which the wavelength 4200Å is absent for the reflected light.
View Solution
Knowledge Check
A ray of light is incident at an angle of 45∘ (ralative to the normal) on a thin film of a liquid with an index of refraction of √2. Assuming that the medium of both sides of the film is air, find the minimum thickness of the film required for constructive interference in the reflected light for sodium light of wavelenght 600 nm.
 A122 nmB212 nmC173 nmD320 nm
A122 nmB212 nmC173 nmD320 nmLight of wavelength 6000Å is reflected at nearly normal incidence from a soap films of refractive index 1.4 The least thickness of the fringe then will appear black is
AinfinityB200ÅC2000ÅD1000ÅWhat is the minimum thickness of a thin film (μ=1.2) that results in constructive interference in the reflected light? If the film is illuminated with light whose wavelength in free space is λ=500nm ?
A104 nmB200 nmC300 nmD400 nm
What is the minimum thickness of a thin film (μ=1.2) that results in constructive interference in the reflected light? If the film is illuminated with light whose wavelength in free space is λ=500nm ?
View SolutionA light of wavelength 5890Å falls normally on a thin air film. The minimum thickness of the film such that the film appears dark in reflected light is
View SolutionA parallel beam of light of wavelength 560 nm falls on a thin film of oil (refractive index = 1.4). What should be the minimum thickness of the film so that it strongly S4 T z reflects the light ?
View SolutionA light of wavelength 5890Å falls normally on a thin air film. The minimum thickness of the film such that the film appears dark in reflected light is
View SolutionA light of wavelength 5890Å falls normally on a thin air film. The minimum thickness of the film such that the film appears dark in reflected light is
View Solution
