In figure S is a monochromatic point source emitting light of wave length λ = 500nm. A thin convex lens of focal length 0.10m is cut into two identical halves L1 and L2 along the principal axis. The two halves are placed symmetrically about the central axis SO with a gap of 0.5 mm. The distance along the axis from S to L1 and L2 is 0.15m while that from L1 andL2 to O is 1.30 m. The screen at O is normal to SO.

(a) If the third intensity maximum occurs at the point A on the screen, find the distance OA. (b) If the gap between L1 and L2 is reduced from its original value of 0.5 mm. Will the distance OA increase, decreases or remain the same?
(a) 1mm, (b) increase
Topper's Solved these Questions
Similar Questions
S is a monochromatic point source emitting light of wavelength l = 500 nm. A thin lens of circular shape and of focal length 0.10 m is cut into two identical halves L1 and L2 by a plane passing through a diameter. The two halves are placed symmetrically about the central axis SO with a gap of 0.5 mm. The distance along the axis from S to L1 and L2 is 0.15 m, while that from L1 and L2 to O is 1.30 m. The screen at O is normal to SO. If the third intensity maximum occurs at point A on the screen, find the distance OA.
View SolutionIn figure S is a monochromatic point source emitting light of wavelength λ=500nm. A thin lens of circular shape and focal length 0.10m is cut into two identical halves L1 and L2 by a plane passing through a doameter. The two halves are placed symmetrically about the central axis SO with a gap of 0.5mm. The distance along the axis from A to L1 and L2 is 0.15m, while that from L1 and L2 to O is 1.30m. The screen at O is normal to SO.
(a) If the 3rd intensity maximum occurs at point P on screen, find distance OP.
(b) If the gap between L1 and L2 is reduced from its original value of 0.5mm, will the distance OP increases, devreases or remain the same?

View Solution
Knowledge Check
If a equiconvex lens of focal length f is cut into two halves by a plane perpendicular to the principal axis, then
AThe focal length of each half becomesf2BThe focal length of each half becomes 2fCThe focal length of each half remains fDThe focal length of each half becomes f4A symmetrical biconvex lens of focal length f is cut into four identical pieces along its principal axis and to the perpendicular to principal axis. The focal length of one of four pieces is
Af4Bf2C2fD4fIf a symmetrical convex lens of focal length 'f is cut into two parts along the principal axis as shown in the figure, the focal length of each part will be:
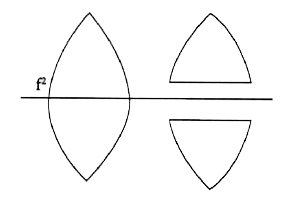 Af2Bf4CfD∞
Af2Bf4CfD∞
In figure S is a monochromatic point source emitting light of wavelength λ=500nm. A thin lens of circular shape and focal length 0.10m is cut into two identical halves L1 and L2 by a plane passing through a doameter. The two halves are placed symmetrically about the central axis SO with a gap of 0.5mm. The distance along the axis from A to L1 and L2 is 0.15m, while that from L1 and L2 to O is 1.30m. The screen at O is normal to SO.
(a) If the 3rd intensity maximum occurs at point P on screen, find distance OP.
(b) If the gap between L1 and L2 is reduced from its original value of 0.5mm, will the distance OP increases, devreases or remain the same?

View SolutionIf a equiconvex lens of focal length f is cut into two halves by a plane perpendicular to the principal axis, then
View SolutionA thin double convex lens of focal length f is broken into two equal halves at the axis. The two halves are combined as shown in figure. What is the focal length of combination in (ii) and (iii).
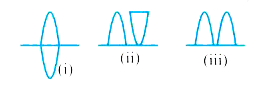
View SolutionFocal length of a convex lens in air is 25 cm. It is cut into two equal halves along its principal axis. What will be the focal length of each half ?
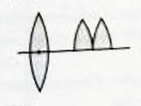
View SolutionA lens is cut from from the optical centre along the principal axis and the two parts of the lens are placed sideways as shown in figure. Then the new focal length of the combination :
View Solution
