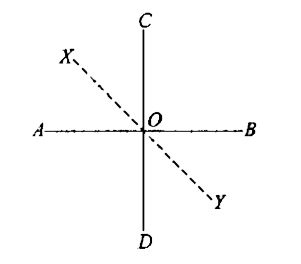
AB and CD are two identical rods each of length l and mass m joined to form a cross. The moment of inertia of these two rods about a bisector (XY) of angle between the rods is

ml212
ml23
2ml23
ml26
The correct Answer is:A
Moment of inertia of rods AB and CD about an axis passing through their point of intersection O and perpendicular to the plane of the rods is
IO=ml212+ml212=ml26
In figure , XY and XY are two mutually perpendicular axes passing through O lying in the plane of the two rods . By symmetry IXY=IX.Y.=I , say
From the theorem of perpendicular axes IXY+IX.Y.=IO
or 2I=ml26orI=ml212

Topper's Solved these Questions
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - CHECK YOUR NEET VITALS
14 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - AIPMT / NEET (MCQs)
37 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - AIPMT / NEET (MCQs)
37 Videos
- LAWS OF MOTIONBOOK - MTG GUIDECHAPTER - LAWS OF MOTIONEXERCISE - AIPMT /NEET (MCQ)
24 Videos
- OSCILLATIONS AND WAVES BOOK - MTG GUIDECHAPTER - OSCILLATIONS AND WAVES EXERCISE - AIPMT / NEET MCQs
43 Videos
Similar Questions
AB and CD are two identical rods each of length l and mass m joined to form a cross. The moment of inertia of these two rods about a bisector (xy) of the angle between the rods is:

View SolutionTwo uniform identicla rods each of mass M and length l are joined to form a cross as shown in figure. Find the momet of inertia of the cross about a bisector as shown doted in the figure

View Solution
Knowledge Check
AB and CD are two indential rods each of length L and mass M joined to from a cross. Find the M.L of the system about a bisector of the angel between the rods (XY):
 AML212BML26CML23D4ML23
AML212BML26CML23D4ML23Two uniform thin identical rods AB and CD each of mass M and length L are joined so as to form a cross as shown. The moment of inertia of the cross about a bisector line EF is :-
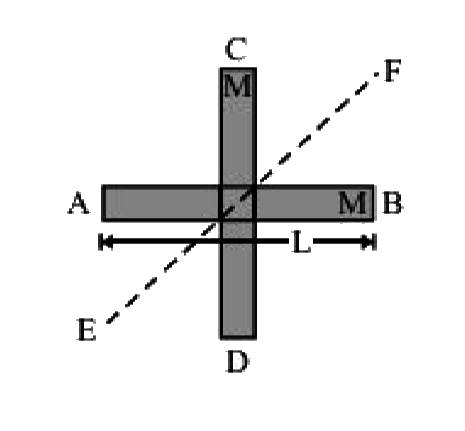 AML26BML24CML212DML23
AML26BML24CML212DML23Three identical thin rods each of length l and mass M are joined together to form a letter H. What is the moment of inertia of the system about one of the sides of H?
A16Ml2B14Ml2C23Ml2D43Ml2
Two uniform identicla rods each of mass M and length l are joined to form a cross as shown in figure. Find the momet of inertia of the cross about a bisector as shown doted in the figure

View SolutionTwo uniform, thin identical rods each of mass M and length l are joined together to form a cross. What will be the moment of inertia of the cross about an axis passing through the point at which the two rods are joined and perpendicular to the plane of the cross ?
View Solutionfour thin rods each of mass m and length l are joined to make a square. Find moment of inertia of all the four rods about any side of the square.
View SolutionTwo uniform thin identical rods AB and CD each of mass M and length L are joined so as to form as cross as shown. The monent of inertia of the cross about a bisector line EF is
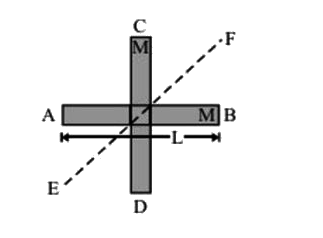
View SolutionTwo uniform, thin identical rods each of mass M and length l are joined together to form a cross. What will be the moment of inertia of the cross about an axis passing through the point at which the two rods are joined and perpendicular to the plane of the cross ?
View Solution
