A block of mass 0.1 kg is pressed EUR against a wall with a horizontal force of 5 N as shown in the figure. If the coefficient of friction between the wall and the block is 0.5, calculate the frictional force acting on the block.

Maximum value of force
of friction =μR
∴fmax=(0.5)5=2.5N
For equilibrium of present case, force of friction upwards
= weight (mg) downwards .
∴ Force of friction =(0.1)×(9.8)=0.98N.
This much friction is possible because it is less than the maximum possible friction i.e., 2.5 N.
∴ Force of friction = 0.98 N
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - MTG GUIDECHAPTER - LAWS OF MOTIONEXERCISE - NEET CAFÉ (TOPICWISE PRACTIVE QUESTIONS) ( NEWTON.S LAWS OF MOTION)
81 Videos
- LAWS OF MOTIONBOOK - MTG GUIDECHAPTER - LAWS OF MOTIONEXERCISE - NEET CAFÉ (TOPICWISE PRACTIVE QUESTIONS) (LAW OF CONSERVATION OF LINEAR MOMENTUM AND ITS APPLICATIONS)
6 Videos
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - AIPMT/ NEET MCQs
31 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - AIPMT / NEET (MCQs)
37 Videos
Similar Questions
A block of mass 1 kg is pressed against a wall by applying a horizontal force of 10N on the block. If the coefficient of friction between the block and the wall is 0.5, magnitude of the frictional force acting on the block is
View SolutionA block of mass 1kg is pressed against a wall by applying a horizontal force of 10N on the block. If the coefficient of friction between the block and the wall is 0.5 ,magnitude of the frictional force acting on the block is
View Solution
Knowledge Check
A block of mass 0.1 kg is held against a wall by applying a horizontal force of 5 N on the block. If the coefficient of friction between the block and the wall is 0.5, then the magnitude of the frictional force acting on the block is
A2.5 NB0.98 NC4.9 ND0.49 NA block of mass 0.1 is held against a wall applying a horizontal force of 5N on block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of the frictional force acting on the block is:
A2.5NB0.98NC4.9ND0.49NA force of 100N is applied on a block of mass 3kg as shown below. The coefficient of friction between wall and the block is 1/4. The friction force acting on the block is :
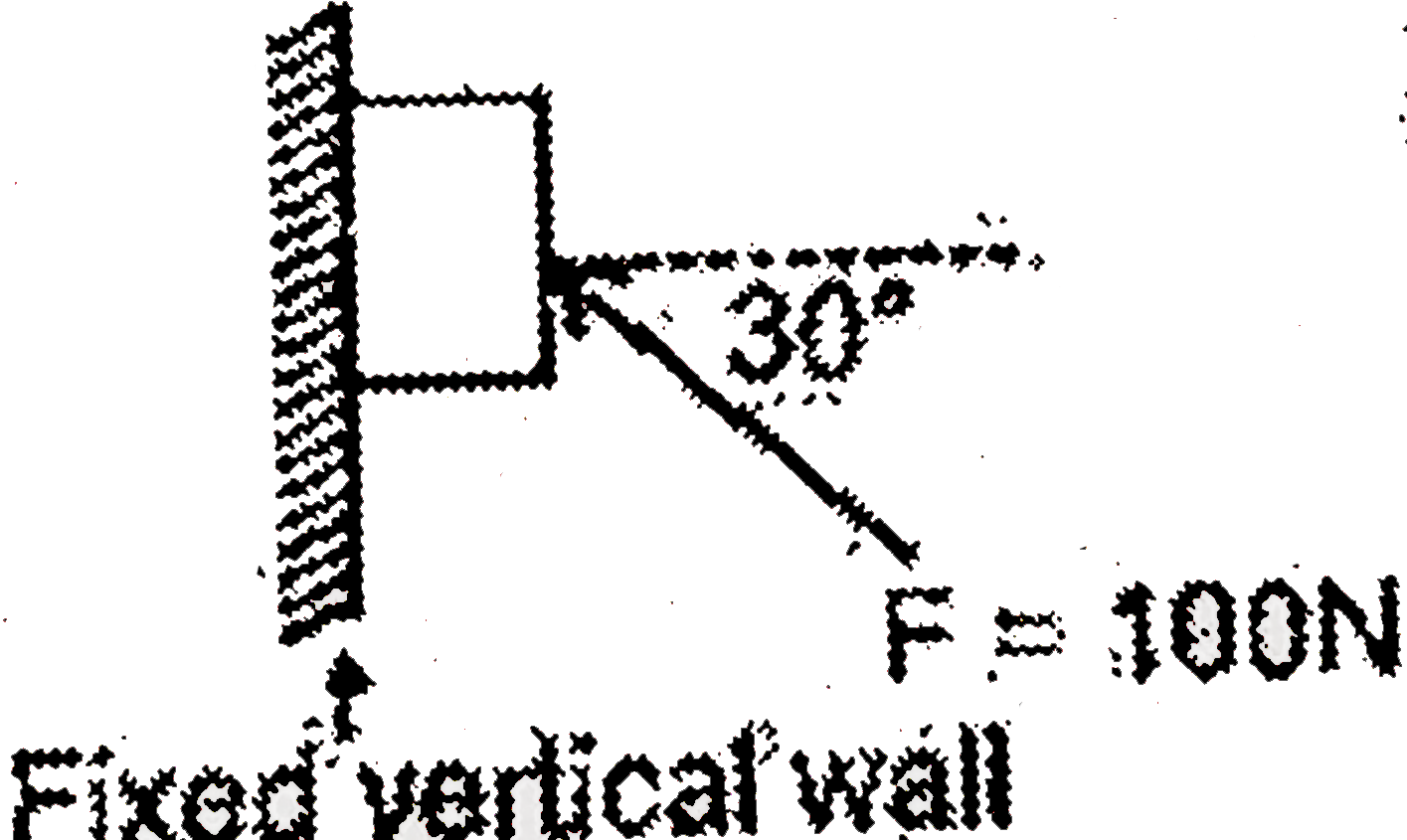 A15 N downwardsB25 N upwardsC20 N downwardsD20 N upwards
A15 N downwardsB25 N upwardsC20 N downwardsD20 N upwards
A block of mass 0.1 kg is held against a wall applying a horizontal force of 5 N on the block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of the frictional force acting on the block is :
View SolutionA block of mass 0.1 is held against a wall applying a horizontal force of 5N on block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of the frictional force acting on the block is:
View SolutionA force of 100 N is applied on a block of mass 3 kg as shown in figure. The coefficient of friction between the surface and the block is 14 .Then the friction force acting on the block is
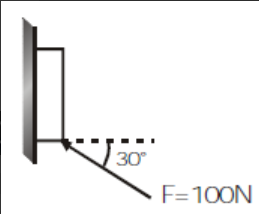
View SolutionA force of 100N is applied on a block of mass 3kg as shown below. The coefficient of friction between wall and the block is 1/4. The friction force acting on the block is :
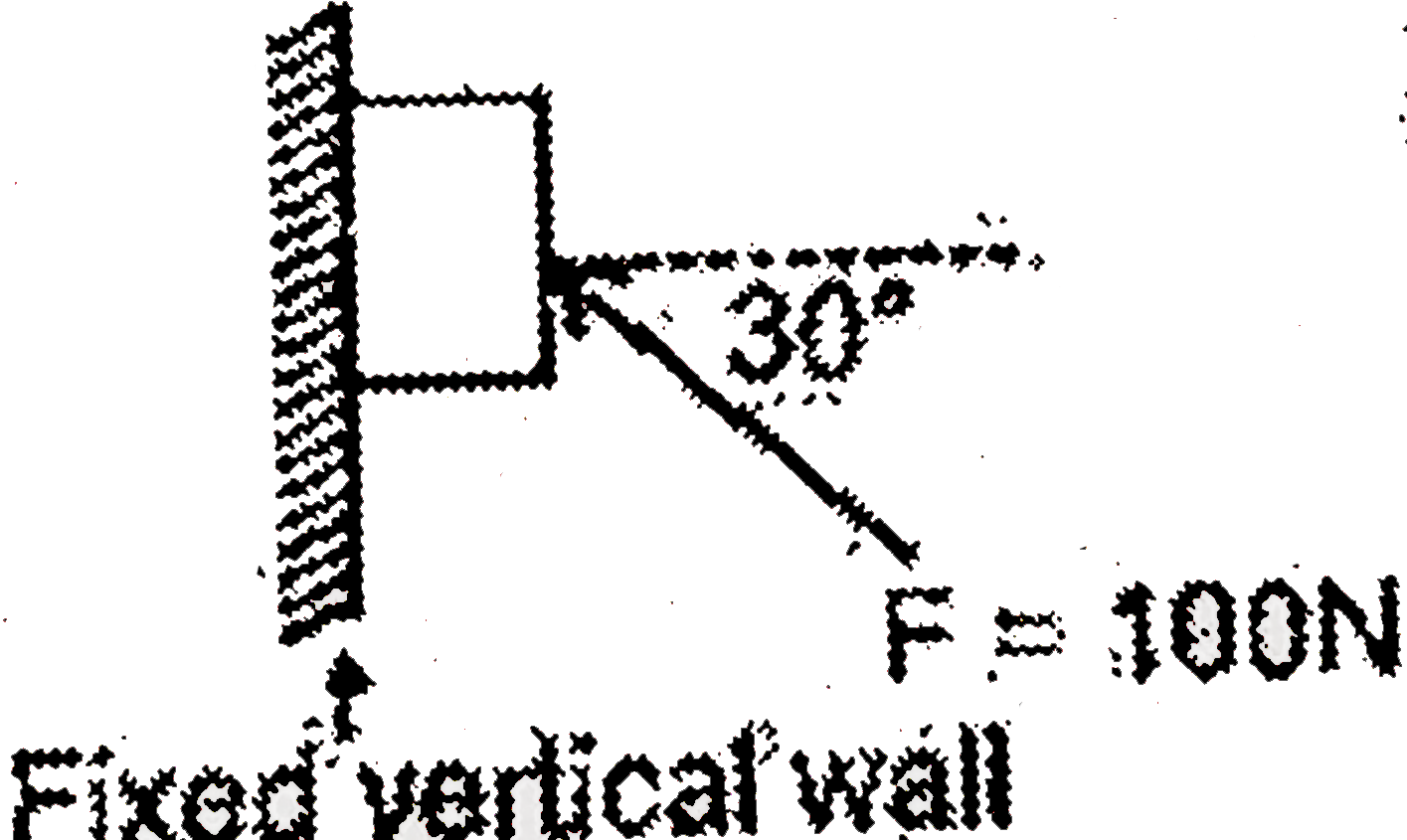
View SolutionIn the arrangement shown in figure coefficient of friction between 5kg block and incline plane is μ=0.5. Friction force acting on the 5kg block is

View Solution
