A block of mass 2 kg initially at rest moves under the action of an applied horizontal force of 6 N on a rough horizontal surface. The coefficient of friction between block and surface is 0.1. The work done by the applied force in 10 s is (Take g=10ms−2)
200J
−200J
600 J
−600J
The correct Answer is:C
To solve the problem step by step, we will follow these calculations:
Step 1: Calculate the frictional force
The frictional force (f) can be calculated using the formula:
f=μ⋅N
Where:
- μ is the coefficient of friction (0.1)
- N is the normal force, which is equal to the weight of the block (mg).
Given:
- Mass m=2kg
- Acceleration due to gravity g=10m/s2
Calculating the normal force:
N=m⋅g=2kg⋅10m/s2=20N
Now, substituting into the frictional force formula:
f=0.1⋅20N=2N
Step 2: Calculate the net force acting on the block
The net force (Fnet) can be calculated by subtracting the frictional force from the applied force:
Fnet=Fapplied−f
Where:
- Fapplied=6N
Substituting the values:
Fnet=6N−2N=4N
Step 3: Calculate the acceleration of the block
Using Newton's second law:
Fnet=m⋅a
We can rearrange this to find acceleration (a):
a=Fnetm
Substituting the values:
a=4N2kg=2m/s2
Step 4: Calculate the displacement of the block in 10 seconds
Using the formula for displacement (s) under constant acceleration:
s=12at2
Substituting the values:
s=12⋅2m/s2⋅(10s)2
s=12⋅2⋅100=100m
Step 5: Calculate the work done by the applied force
The work done (W) by the applied force can be calculated using the formula:
W=Fapplied⋅s⋅cos(θ)
Where:
- θ=0∘ (since the force and displacement are in the same direction, cos(0∘)=1)
Substituting the values:
W=6N⋅100m⋅1
W=600J
Final Answer
The work done by the applied force in 10 seconds is 600 Joules.
---
The frictional force (f) can be calculated using the formula:
f=μ⋅N
Where:
- μ is the coefficient of friction (0.1)
- N is the normal force, which is equal to the weight of the block (mg).
- Mass m=2kg
- Acceleration due to gravity g=10m/s2
N=m⋅g=2kg⋅10m/s2=20N
f=0.1⋅20N=2N
The net force (Fnet) can be calculated by subtracting the frictional force from the applied force:
Fnet=Fapplied−f
Where:
- Fapplied=6N
Fnet=6N−2N=4N
Using Newton's second law:
Fnet=m⋅a
We can rearrange this to find acceleration (a):
a=Fnetm
a=4N2kg=2m/s2
Using the formula for displacement (s) under constant acceleration:
s=12at2
s=12⋅2m/s2⋅(10s)2
s=12⋅2⋅100=100m
The work done (W) by the applied force can be calculated using the formula:
W=Fapplied⋅s⋅cos(θ)
Where:
- θ=0∘ (since the force and displacement are in the same direction, cos(0∘)=1)
W=6N⋅100m⋅1
W=600J
The work done by the applied force in 10 seconds is 600 Joules.
Topper's Solved these Questions
- WORK , ENERGY AND POWERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WORK , ENERGY AND POWEREXERCISE - NCERT
18 Videos
- WORK , ENERGY AND POWERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WORK , ENERGY AND POWEREXERCISE - ASSERTION & REASON
15 Videos
- WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVESEXERCISE - Assertion And Reason
15 Videos
Similar Questions
A body of mass 2 kg initially at rest moves under the action of an applied horizontal force of 7N on a table with coefficient of kinetic friction =0.1. Calculate the
(a) work done by applied force in 10s. (b) work done by friction in 10s.
(c ) work done by the net force on the body in 10s.
(d) change in K.E. of body in 10s, and interpret your result.
View SolutionA force of 10N is acting on a block of 20kg on horizontal surface with coefficient of friction μ=0.2. Calculate the work done by the force.
View Solution
Knowledge Check
A block of mass 2kg initially at rest moves under the action of an applied horizontal force of 6 N on a rough horizontal surface. The coefficient of friction between the block and surface is 0.1. the work done by friction in 10 s is
A200JB−200JC600 JD−600JTwo blocks A and B of masses 10 kg and 15 kg are placed in contact with each other rest on a rough horizontal surface as shown in the figure. The coefficient of friction between the blocks and surface is 0.2. A horizontal force of 200 N is applied to block A. The acceleration of the system is (Take g=10ms−2)
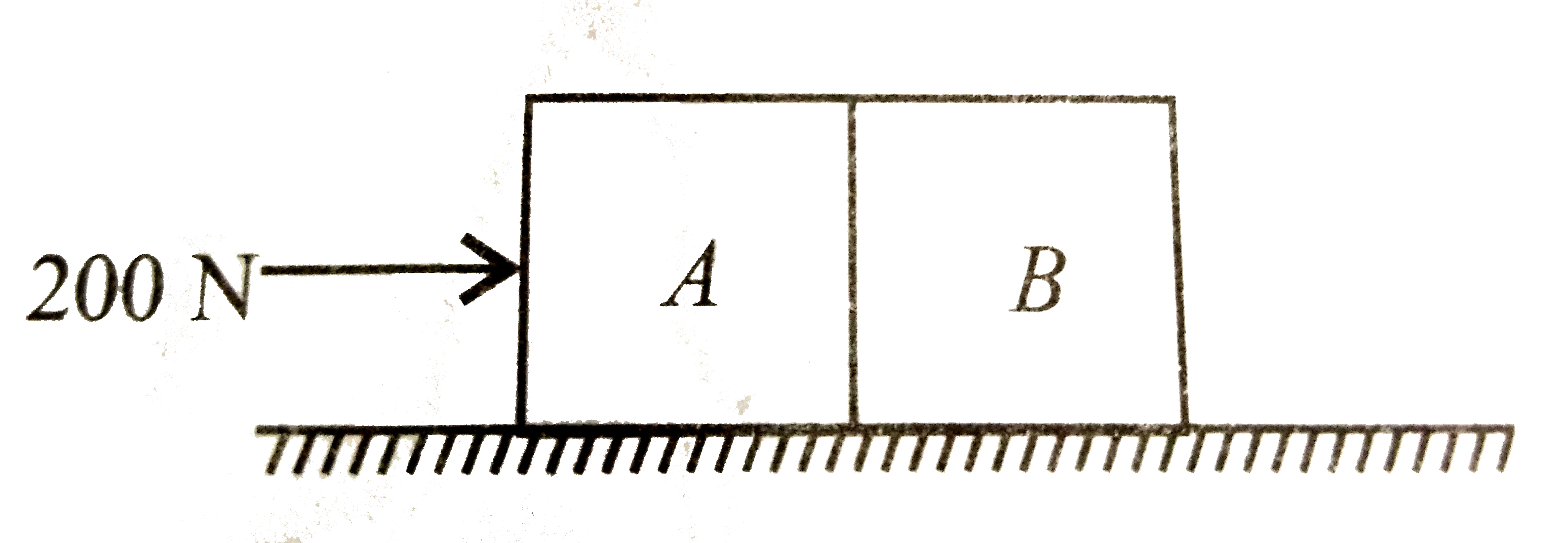 A4ms−2B6ms−2C8ms−2D10ms−2
A4ms−2B6ms−2C8ms−2D10ms−2
A block of mass 50 kg slides over a horizontal distance of 1m. If the coefficient of friction between their surface is 0.2, then work done against friction is (take g=9.8m/s2) :
View SolutionA force of 49 N just able to move a block of wood weighing 10 kg on a rough horizontal surface , then coefficient of friction is
View SolutionA block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
View SolutionA block of mass m is kept over another block of mass 2 m and the system rests on a smooth horizontal surface. The coefficient of friction between the blocks is 0.50. Find the work done by the force of friction on the smaller block by the bigger block during a displacement d of the system, when a force mg is applied to the lower block.
View SolutionA block is kept on a rough horizontal surface as shown. Its mass is 2 kg and coefficient of friction between block and surface (μ)=0.5. A horizontal force F is acting on the block. When

View SolutionA body of mass 10kg is under the action of 138N on the horizontal surface. If coefficient of friction in between the surfaces is one, the distance it travels in 10s in metre is
View Solution
