A block of mass m is kept over another block of mass 2 m and the system rests on a smooth horizontal surface. The coefficient of friction between the blocks is 0.50. Find the work done by the force of friction on the smaller block by the bigger block during a displacement d of the system, when a force mg is applied to the lower block.
mgd3
mgd
mgd2
Zero
To find the work done by the force of friction on the smaller block during a displacement d of the system, we can follow these steps:
Step 1: Understand the System
We have two blocks:
- A smaller block of mass m on top of a larger block of mass 2m.
- The system is on a smooth horizontal surface (meaning there is no friction with the ground).
- The coefficient of friction between the two blocks is μ=0.50.
Step 2: Identify the Applied Force
A force F=mg is applied to the lower block (mass 2m).
Step 3: Calculate the Acceleration of the System
The total mass of the system is:
Mtotal=m+2m=3m
The acceleration a of the system can be calculated using Newton's second law:
a=FMtotal=mg3m=g3
Step 4: Calculate the Frictional Force
The frictional force f acting on the smaller block (mass m) is responsible for its acceleration. According to Newton's second law:
f=m⋅a=m⋅g3=mg3
Step 5: Determine the Maximum Frictional Force
The maximum static frictional force fmax that can act between the blocks is given by:
fmax=μ⋅N=μ⋅mg=0.5⋅mg=mg2
Step 6: Compare the Forces
Since mg3<mg2, the frictional force mg3 is less than the maximum static friction. Therefore, the blocks will move together without slipping.
Step 7: Calculate the Work Done by Friction
The work done W by the frictional force on the smaller block during the displacement d is given by:
W=f⋅d=(mg3)⋅d=mgd3
Final Answer
Thus, the work done by the force of friction on the smaller block during the displacement d is:
W=mgd3
---
We have two blocks:
- A smaller block of mass m on top of a larger block of mass 2m.
- The system is on a smooth horizontal surface (meaning there is no friction with the ground).
- The coefficient of friction between the two blocks is μ=0.50.
A force F=mg is applied to the lower block (mass 2m).
The total mass of the system is:
Mtotal=m+2m=3m
The acceleration a of the system can be calculated using Newton's second law:
a=FMtotal=mg3m=g3
The frictional force f acting on the smaller block (mass m) is responsible for its acceleration. According to Newton's second law:
f=m⋅a=m⋅g3=mg3
The maximum static frictional force fmax that can act between the blocks is given by:
fmax=μ⋅N=μ⋅mg=0.5⋅mg=mg2
Since mg3<mg2, the frictional force mg3 is less than the maximum static friction. Therefore, the blocks will move together without slipping.
The work done W by the frictional force on the smaller block during the displacement d is given by:
W=f⋅d=(mg3)⋅d=mgd3
Thus, the work done by the force of friction on the smaller block during the displacement d is:
W=mgd3
Similar Questions
A block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
View SolutionA 2kg block is placed over a 5kg block and both are placed on a smooth horizontal surface. The coefficient of friction between the blocks is 0.10. Find the acceleration of the two blocks if a horizontal force of 14N is applied to the upper block (g = 10ms−2).
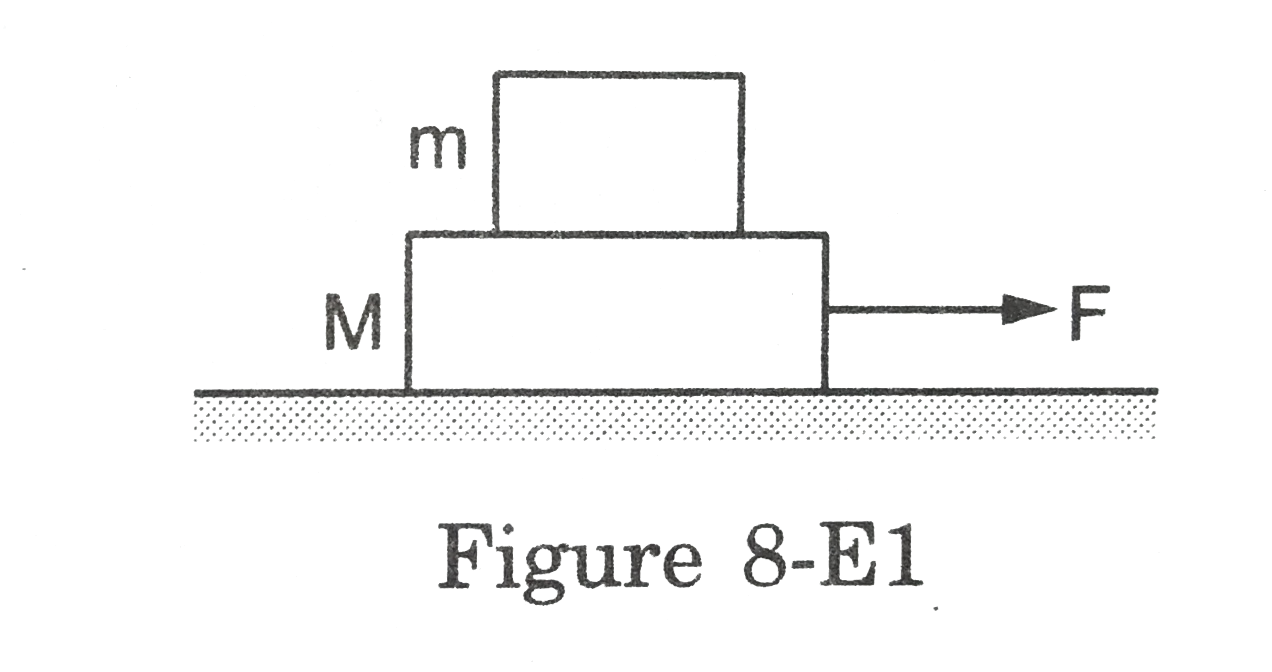
View SolutionA block of mass m is kept over another block of mass M nd the system rests on a horizontal force F acting on the lower block produces an accelertion F2(m+M) in the system the two blocks always move together. A. Find the coefficient of kinetic frictioin between the bigger block and th horizontal surface. b. find the frictional force acting on the smaller block. c. Find the work done by the force of friction on the smaller block by the bigger block during a displacement d of the system.
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
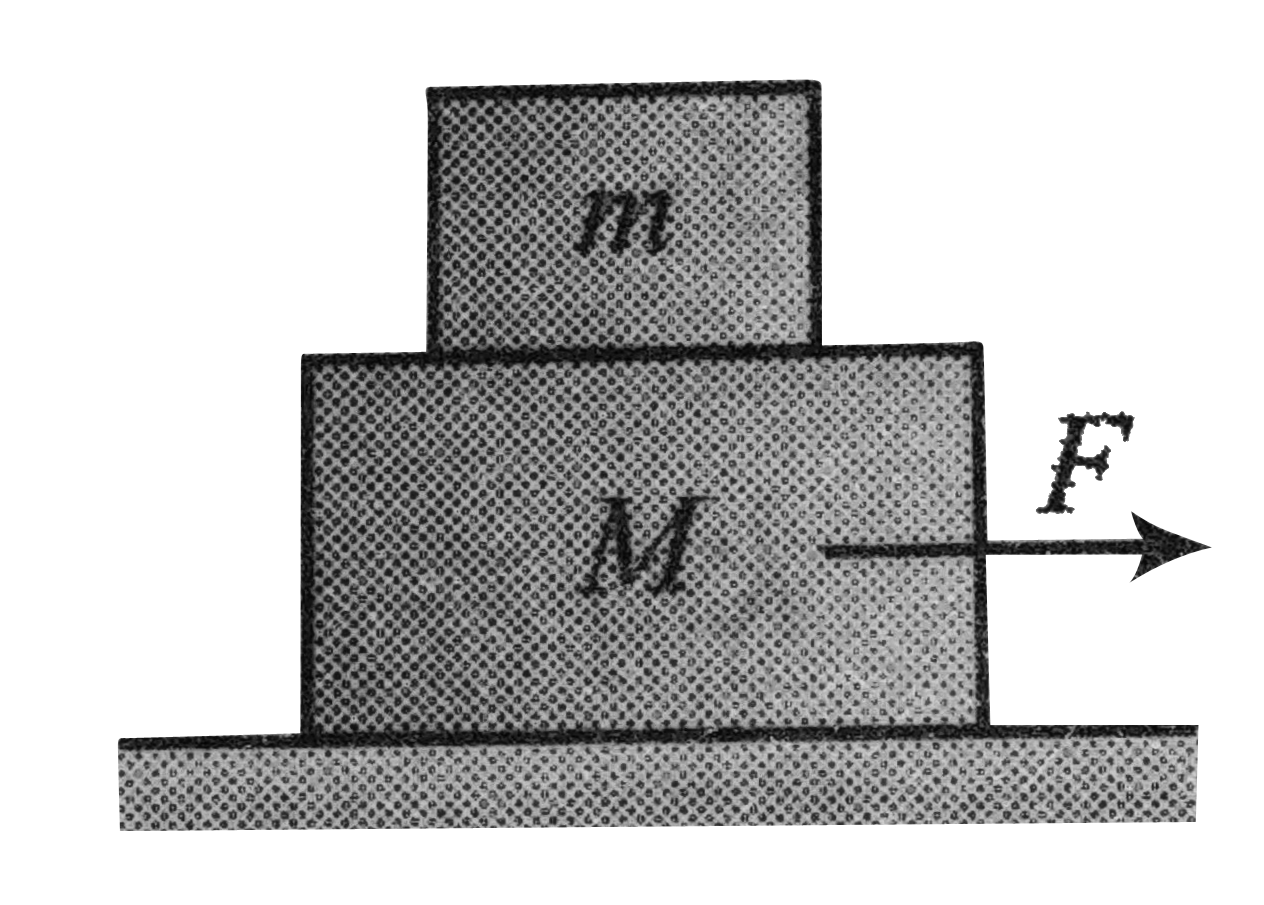
View SolutionA block of mass m is kept over another block of mass M and the system rests on a horizontal surface. A constant horizontal force F acting on the lower block produces an acceleration F2(m+M) in the sytem. The two blocks always move together. Consider displacement d of the system.
a. Find the work done by friction on bigger block.
b. Find the coefficient of kinetic friction between the bigger block and the horizontal surface.
c. Find the frictional acting on the smaller block.
d. Find the work done by the force of friction on the smaller block by the bigger block.
e. Find the work done by static friction on bigger block.
View SolutionA block of mass m is slowly pulled along a curved surface from position 1 and 2. If the coefficient of kinetic friction between the block and surface is μ, find the work done by the applied force.

View SolutionA block A of mass 2kg is placed over smooth block B of mass 4kg which is placed over a smooth horizontal floor The coefficient of friction between A and B is 0.4 when a horizontal forces of magnitude 10N is applied on A the acceleration of block of A and B are

View SolutionA block of mass m is pulled by a force of constant power P placed on a rough horizontal plane. The friction coefficient between the block and the surface is μ. Then
View SolutionA 3 kg block is placed over a 10 kg block and both are palced on a smooth horizontal surface. The coefficient of friction between the block is 0.2 . If a horizontal force of 20 N is applied to 3 kg block, accelerations of the two block in ms−2 are (take, g=ms−2)

View SolutionA small block of mass 20kg rests on a bigger block of mass 30kg, which lies on a smooth horizontal plane. Initially the whole system is at rest. The coefficient of friction between the blocks is 0.5. The horizontal force F=50N is applied on the lower block.
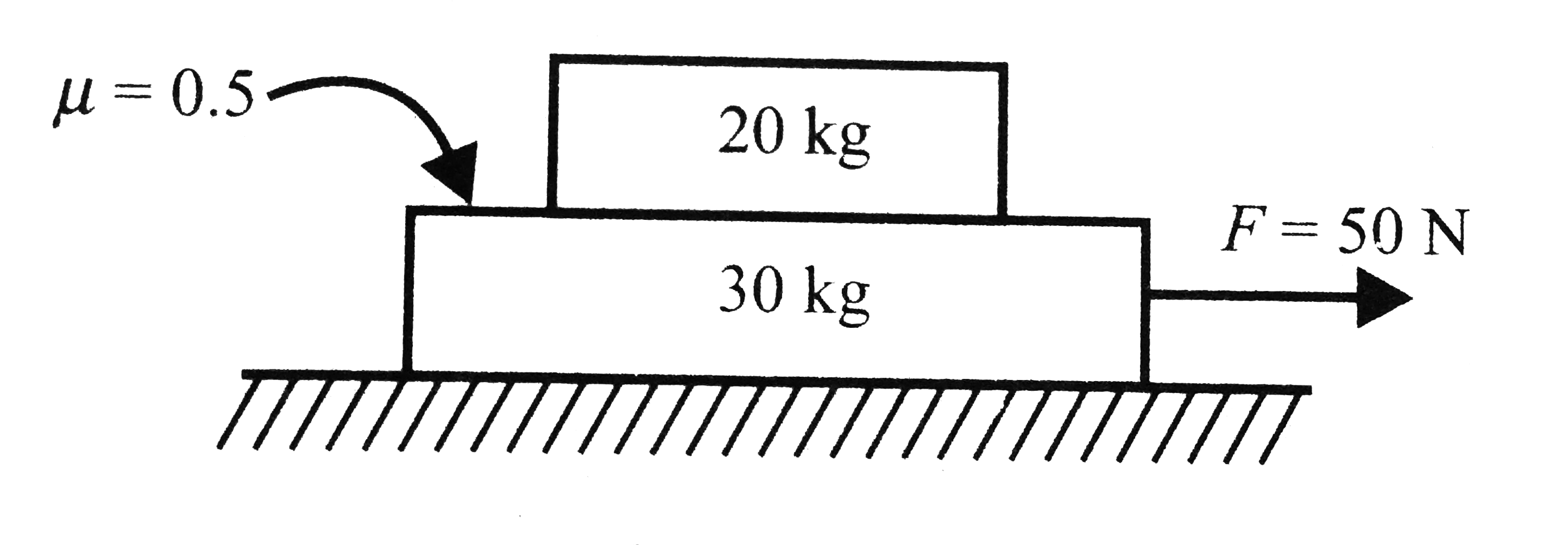
a. Find the work done by fricitonal force on upper block and on the lower block in t=2s.
b. Is the magnitude of work done by the frictional force on upper and lower blocks same?
c. Is the work done by the frictional force on the upper block converted to heat or mechanical energy or both?
View Solution