A block of mass 2kg initially at rest moves under the action of an applied horizontal force of 6 N on a rough horizontal surface. The coefficient of friction between the block and surface is 0.1. the work done by friction in 10 s is
1) 200J
2) −200J
3) 600 J
4) −600J
The correct Answer is:B
To solve the problem step by step, we will follow these calculations:
Step 1: Identify the forces acting on the block
- The block has a mass m=2kg.
- An applied horizontal force Fapplied=6N.
- The coefficient of friction μ=0.1.
- The gravitational acceleration g=10m/s2.
Step 2: Calculate the normal force
Since the block is on a horizontal surface, the normal force N is equal to the weight of the block:
N=mg=2kg×10m/s2=20N
Step 3: Calculate the frictional force
The frictional force Ffriction can be calculated using the formula:
Ffriction=μN=0.1×20N=2N
Step 4: Calculate the net force acting on the block
The net force Fnet acting on the block is given by:
Fnet=Fapplied−Ffriction=6N−2N=4N
Step 5: Calculate the acceleration of the block
Using Newton's second law, we can find the acceleration a:
Fnet=ma⟹4N=2kg×a⟹a=4N2kg=2m/s2
Step 6: Calculate the displacement of the block in 10 seconds
Using the formula for displacement s:
s=12at2=12×2m/s2×(10s)2=12×2×100=100m
Step 7: Calculate the work done by friction
The work done by the frictional force Wfriction is given by:
Wfriction=Ffriction×s×cos(θ)
Since the frictional force acts in the opposite direction to the displacement, θ=180∘ and cos(180∘)=−1:
Wfriction=2N×100m×(−1)=−200J
Final Answer
The work done by friction in 10 seconds is −200J.
---
- The block has a mass m=2kg.
- An applied horizontal force Fapplied=6N.
- The coefficient of friction μ=0.1.
- The gravitational acceleration g=10m/s2.
Since the block is on a horizontal surface, the normal force N is equal to the weight of the block:
N=mg=2kg×10m/s2=20N
The frictional force Ffriction can be calculated using the formula:
Ffriction=μN=0.1×20N=2N
The net force Fnet acting on the block is given by:
Fnet=Fapplied−Ffriction=6N−2N=4N
Using Newton's second law, we can find the acceleration a:
Fnet=ma⟹4N=2kg×a⟹a=4N2kg=2m/s2
Using the formula for displacement s:
s=12at2=12×2m/s2×(10s)2=12×2×100=100m
The work done by the frictional force Wfriction is given by:
Wfriction=Ffriction×s×cos(θ)
Since the frictional force acts in the opposite direction to the displacement, θ=180∘ and cos(180∘)=−1:
Wfriction=2N×100m×(−1)=−200J
The work done by friction in 10 seconds is −200J.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WORK , ENERGY AND POWEREXERCISE - NCERT18videos
WORK , ENERGY AND POWER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WORK , ENERGY AND POWEREXERCISE - ASSERTION & REASON15videos
WORK , ENERGY AND POWER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVESEXERCISE - Assertion And Reason15videos
WAVES
Similar Questions
A body of mass 2 kg initially at rest moves under the action of an applied horizontal force of 7N on a table with coefficient of kinetic friction =0.1. Calculate the
(a) work done by applied force in 10s. (b) work done by friction in 10s.
(c ) work done by the net force on the body in 10s.
(d) change in K.E. of body in 10s, and interpret your result.View SolutionA block of mass m is kept over another block of mass 2 m and the system rests on a smooth horizontal surface. The coefficient of friction between the blocks is 0.50. Find the work done by the force of friction on the smaller block by the bigger block during a displacement d of the system, when a force mg is applied to the lower block.
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass 2 kg initially at rest moves under the action of an applied horizontal force of 6 N on a rough horizontal surface. The coefficient of friction between block and surface is 0.1. The work done by the applied force in 10 s is (Take g=10ms−2)
A200JB−200JC600 JD−600J - Question 2 - Select One
Two blocks A and B of masses 10 kg and 15 kg are placed in contact with each other rest on a rough horizontal surface as shown in the figure. The coefficient of friction between the blocks and surface is 0.2. A horizontal force of 200 N is applied to block A. The acceleration of the system is (Take g=10ms−2)
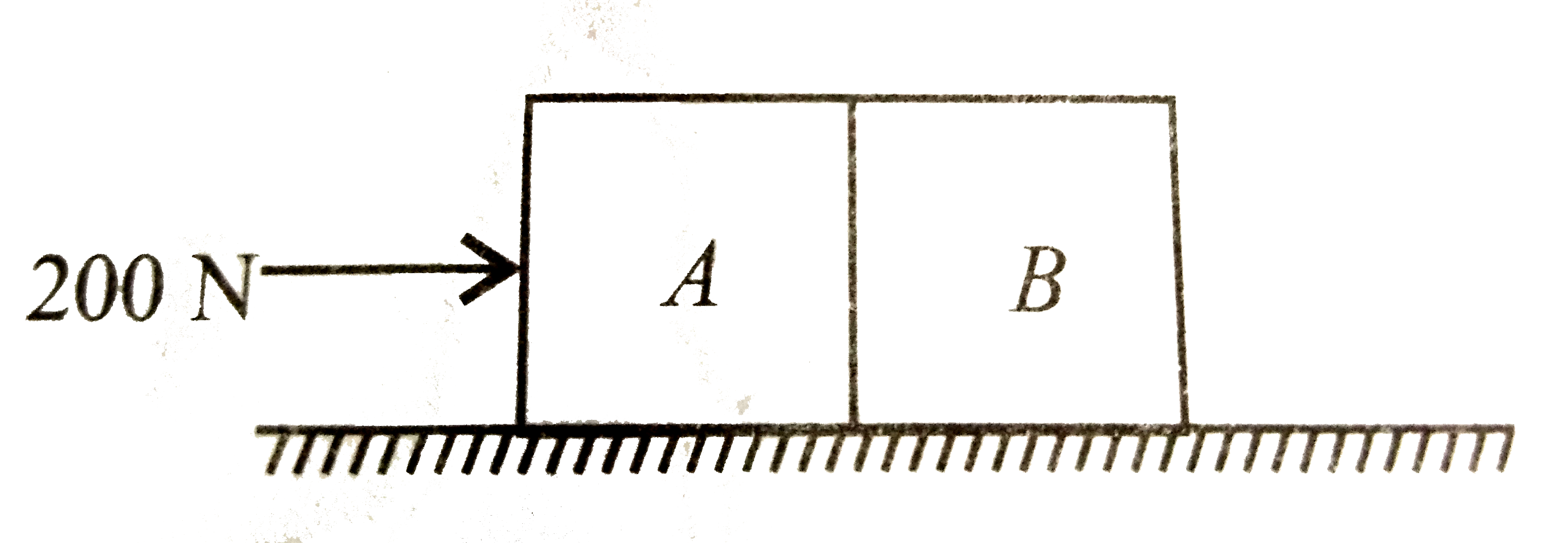 A4ms−2B6ms−2C8ms−2D10ms−2
A4ms−2B6ms−2C8ms−2D10ms−2
A block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
View SolutionA force of 10N is acting on a block of 20kg on horizontal surface with coefficient of friction μ=0.2. Calculate the work done by the force.
View SolutionA block of mass 50 kg slides over a horizontal distance of 1m. If the coefficient of friction between their surface is 0.2, then work done against friction is (take g=9.8m/s2) :
View SolutionA force of 49 N just able to move a block of wood weighing 10 kg on a rough horizontal surface , then coefficient of friction is
View SolutionA block of mass 1 kg is pressed against a wall by applying a horizontal force of 10N on the block. If the coefficient of friction between the block and the wall is 0.5, magnitude of the frictional force acting on the block is
View SolutionA body of mass 10kg is under the action of 138N on the horizontal surface. If coefficient of friction in between the surfaces is one, the distance it travels in 10s in metre is
View Solution

