In the question number 25, if the mass placed at vertex A is doubled, then the force acting on the mass 2m placed at the centroid O is
zero
2Gm2l2
5Gm2l2
6Gm2l2
The correct Answer is:D
To solve the problem, we need to analyze the forces acting on the mass 2m placed at the centroid O of a triangle when the mass at vertex A is doubled.
1. Identify the Initial Setup:
- Let the mass at vertex A be m.
- The masses at vertices B and C remain unchanged.
- The mass at the centroid O is 2m.
2. Determine the Forces Acting on Mass at Centroid:
- The gravitational force acting on the mass at vertex A (now 2m) is given by:
FOA=G⋅2m⋅md2OA
- The distances dOA, dOB, and dOC are the distances from the centroid to the vertices A, B, and C respectively. For an equilateral triangle, these distances can be calculated as:
dOA=L√3,dOB=dOC=L√3
- Thus, the force due to mass at vertex A becomes:
FOA=G⋅2m⋅m(L√3)2=2Gm2⋅3L2=6Gm2L2
3. Calculate Forces from Masses at Vertices B and C:
- The gravitational force due to mass at vertex B and C (both are m) is:
FOB=FOC=G⋅m⋅2m(L√3)2=G⋅2m2⋅3L2=6Gm2L2
4. Determine the Resultant Forces:
- The forces FOB and FOC act in opposite directions to FOA.
- The net force acting on mass 2m at centroid O is:
Fnet=FOA−(FOB+FOC)=6Gm2L2−(6Gm2L2+6Gm2L2)
- Simplifying this gives:
Fnet=6Gm2L2−12Gm2L2=−6Gm2L2
5. Final Result:
- The negative sign indicates that the net force is directed towards the centroid O. Therefore, the force acting on the mass 2m placed at the centroid O is:
Fnet=6Gm2L2
- Let the mass at vertex A be m.
- The masses at vertices B and C remain unchanged.
- The mass at the centroid O is 2m.
- The gravitational force acting on the mass at vertex A (now 2m) is given by:
FOA=G⋅2m⋅md2OA
- The distances dOA, dOB, and dOC are the distances from the centroid to the vertices A, B, and C respectively. For an equilateral triangle, these distances can be calculated as:
dOA=L√3,dOB=dOC=L√3
- Thus, the force due to mass at vertex A becomes:
FOA=G⋅2m⋅m(L√3)2=2Gm2⋅3L2=6Gm2L2
- The gravitational force due to mass at vertex B and C (both are m) is:
FOB=FOC=G⋅m⋅2m(L√3)2=G⋅2m2⋅3L2=6Gm2L2
- The forces FOB and FOC act in opposite directions to FOA.
- The net force acting on mass 2m at centroid O is:
Fnet=FOA−(FOB+FOC)=6Gm2L2−(6Gm2L2+6Gm2L2)
- Simplifying this gives:
Fnet=6Gm2L2−12Gm2L2=−6Gm2L2
- The negative sign indicates that the net force is directed towards the centroid O. Therefore, the force acting on the mass 2m placed at the centroid O is:
Fnet=6Gm2L2
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - The Gravitational constant8videos
GRAVITATION
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Acceleration due to gravity below and above the surface of earth8videos
GRAVITATION
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Assertion And Reason15videos
GRAVITATION
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason10videos
KINETIC THEORY
Similar Questions
Three equal masses 2m each are placed at the vertices an equilateral triangle PQR
(i) What is the force acting on a mass m placed at the centroid G of the triangle ?
(ii) What is the force on mass m if the mass at the vertex P is quadrupled ?
Take PG = QG = RG = 1m
 View Solution
View SolutionThree equal masses of mkg each are fixed at the vertices of an equilateral triangle ABC.
a. What is the force acting on a mass 2m placed at the centroid G of the triangle?
b. What is the force if the mass at the vertex A is doubled? Take AG=BG=CG=1m
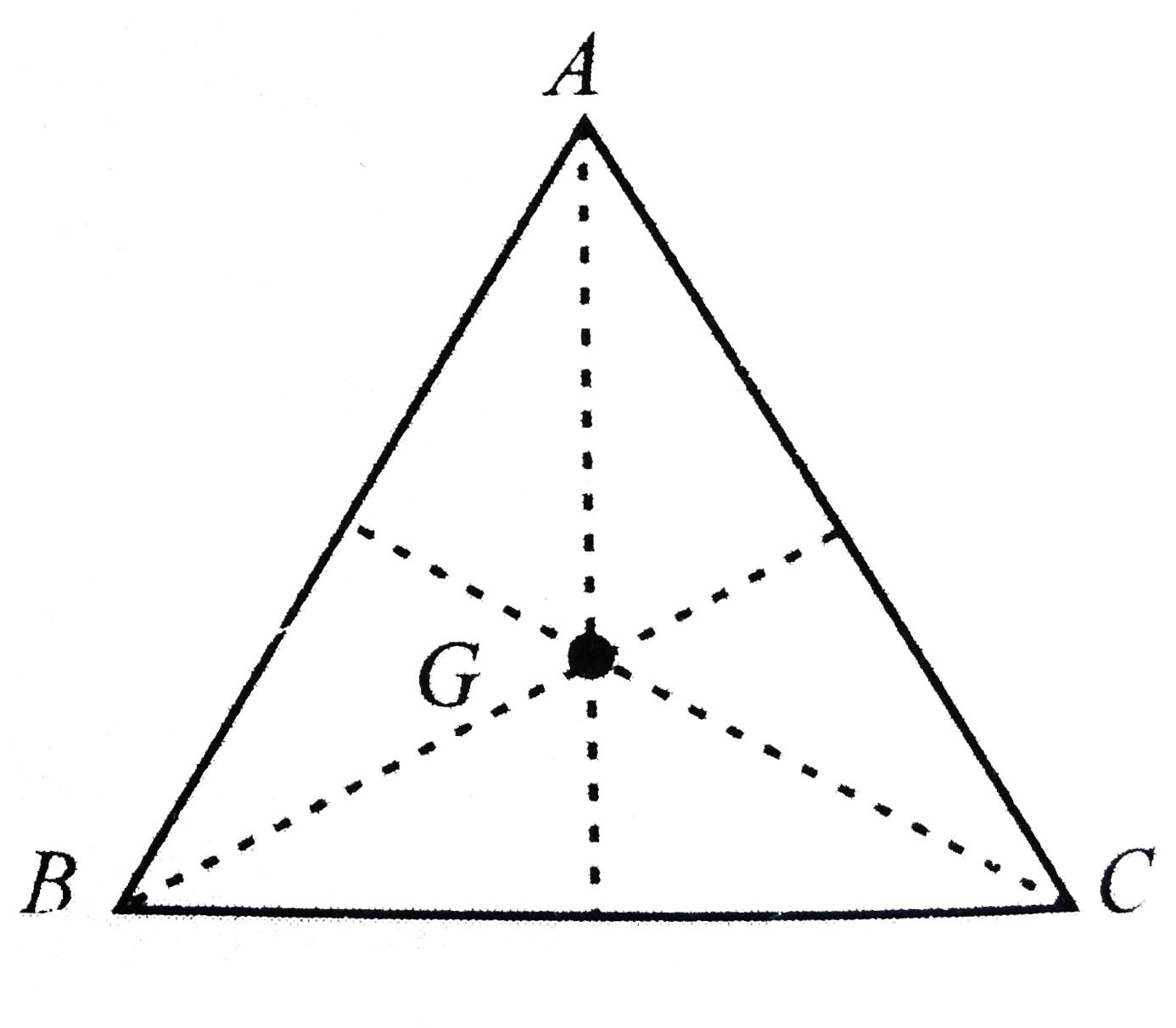 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Three masses each of mass m are palced at the vertices of an equilateral triangles ABC of side l as shown in figure. The force acting on a mass 2m placed at the centroid O of the triangle is
 AzeroB3Gm2l2C5Gm2l2D7Gm2l2
AzeroB3Gm2l2C5Gm2l2D7Gm2l2
Four particles having masses, m, 2m, 3m, and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the center.
View SolutionFour particles having masses, m, 2m, 3m, and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the centre.
View SolutionFour particles having masses, m, 2m, 3m, and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the centre.
View SolutionThree equal masses of 1.5 kg each are fixed at the vertices of an equilateral triangle of side 1 m. What is the force acting on a particle of mass 1 kg placed at its centroid ?
View SolutionThree masses of 1 kg each are kept at the vertices of an equilateral triangle of side 3 m. What is the force acting on a point mass of 5 kg placed at its centroid ?
View SolutionWe know that when two equal masses are placed on a line then, gravitational force on a third mass is zero due to these two masses when the third is placed at the centre of line joining the two masses. But if third mass is placed anywhere else on the x-axis, the gravitational force acts on that mass due to these two masses. Consider a system shown in figure.
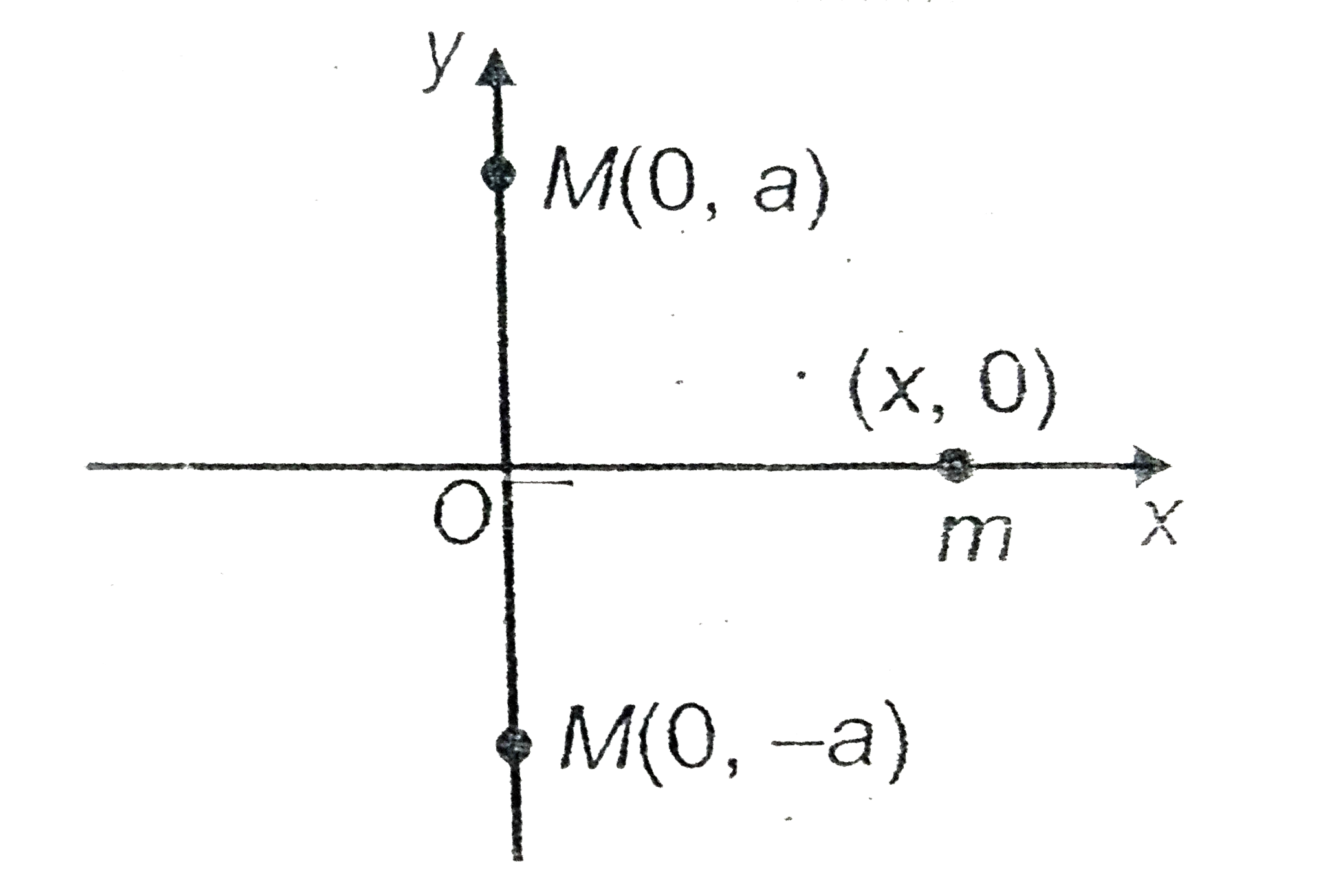
In this system two point masses of mass M each are placed at y-axis at a distance a from origin and these masses are fixed. If a third point mass of mass m is released at a distance x from origin on x-axis, then answer the following questions.
The distance between positions of maximum force on mass m isView SolutionWe know that when two equal masses are placed on a line then, gravitational force on a third mass is zero due to these two masses when the third is placed at the centre of line joining the two masses. But if third mass is placed anywhere else on the x-axis, the gravitational force acts on that mass due to these two masses. Consider a system shown in figure.
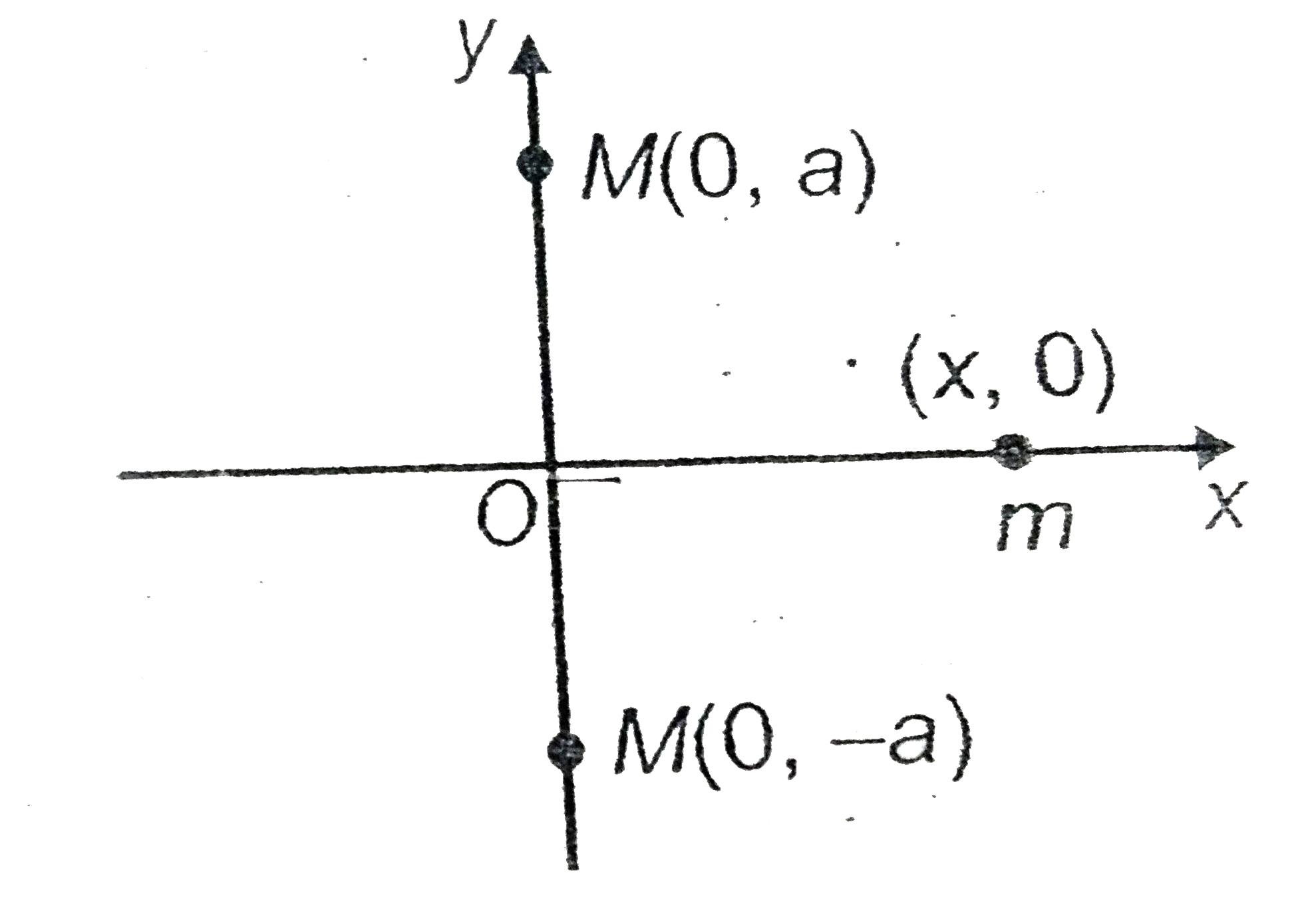
In this system two point masses of mass M each are placed at y-axis at a distance a from origin and these masses are fixed. If a third point mass of mass m is released at a distance x from origin on x-axis, then answer the following questions.
Which of the following graphs best represents the variation of force on mass m with distance x ?View Solution

