To what height should a cyclindrical vessel be filled with a homogeneous liquid to make the force with which the liquid pressure on the sides of the vessel equal to the force exerted by the liquid on the bottom of the vessel ?
equal to the radius
less than radius
more than radius
four times of radius
The correct Answer is:A
To solve the problem of determining the height to which a cylindrical vessel should be filled with a homogeneous liquid so that the force exerted by the liquid on the sides of the vessel equals the force exerted by the liquid on the bottom of the vessel, we can follow these steps:
1. Define Variables:
- Let H be the height of the liquid in the cylinder.
- Let r be the radius of the cylinder.
- Let ρ be the density of the liquid.
- Let g be the acceleration due to gravity.
2. Calculate the Weight of the Liquid:
- The volume of the liquid in the cylindrical vessel is given by V=πr2H.
- The weight of the liquid, W, can be calculated using the formula:
W=Volume×Density×g=V⋅ρ⋅g=πr2Hρg
- Name this equation as Equation 1:
W=πr2Hρg
3. Calculate the Force Exerted by the Liquid on the Bottom:
- The pressure at the bottom of the vessel due to the liquid column is given by:
P=ρgH
- The area of the bottom of the cylinder is A=πr2.
- Therefore, the force Fb exerted by the liquid on the bottom is:
Fb=P⋅A=(ρgH)⋅(πr2)=πr2ρgH
4. Calculate the Force Exerted by the Liquid on the Sides:
- The mean pressure on the sides of the vessel is given by the average pressure, which is ρgH2 (since pressure varies linearly from 0 at the top to ρgH at the bottom).
- The total force Fs exerted by the liquid on the sides of the vessel is:
Fs=Mean Pressure×Area of the sides=(ρgH2)⋅(2πrH)=πrHρgH
- Name this equation as Equation 2:
Fs=πrH2ρg
5. Set the Forces Equal:
- To find the height H such that the force on the sides equals the force on the bottom, we set Fs=W:
πrH2ρg=πr2Hρg
6. Simplify the Equation:
- Cancel out common terms (π, ρ, g, and one r):
H2=rH
7. Solve for Height H:
- Rearranging gives:
H2−rH=0
- Factoring out H:
H(H−r)=0
- This gives us two solutions: H=0 or H=r. Since H=0 is not meaningful in this context, we have:
H=r
Conclusion:
The height to which the cylindrical vessel should be filled with the liquid is equal to the radius of the cylinder:
H=r
- Let H be the height of the liquid in the cylinder.
- Let r be the radius of the cylinder.
- Let ρ be the density of the liquid.
- Let g be the acceleration due to gravity.
- The volume of the liquid in the cylindrical vessel is given by V=πr2H.
- The weight of the liquid, W, can be calculated using the formula:
W=Volume×Density×g=V⋅ρ⋅g=πr2Hρg
- Name this equation as Equation 1:
W=πr2Hρg
- The pressure at the bottom of the vessel due to the liquid column is given by:
P=ρgH
- The area of the bottom of the cylinder is A=πr2.
- Therefore, the force Fb exerted by the liquid on the bottom is:
Fb=P⋅A=(ρgH)⋅(πr2)=πr2ρgH
- The mean pressure on the sides of the vessel is given by the average pressure, which is ρgH2 (since pressure varies linearly from 0 at the top to ρgH at the bottom).
- The total force Fs exerted by the liquid on the sides of the vessel is:
Fs=Mean Pressure×Area of the sides=(ρgH2)⋅(2πrH)=πrHρgH
- Name this equation as Equation 2:
Fs=πrH2ρg
- To find the height H such that the force on the sides equals the force on the bottom, we set Fs=W:
πrH2ρg=πr2Hρg
- Cancel out common terms (π, ρ, g, and one r):
H2=rH
- Rearranging gives:
H2−rH=0
- Factoring out H:
H(H−r)=0
- This gives us two solutions: H=0 or H=r. Since H=0 is not meaningful in this context, we have:
H=r
The height to which the cylindrical vessel should be filled with the liquid is equal to the radius of the cylinder:
H=r
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Higher Order Thinking Skills8videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Exemplar Problems5videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assertion And Reason15videos
LAWS OF MOTION
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assertion And Reason15videos
MECHANICAL PROPERTIES OF SOLIDS
Similar Questions
To what height h should a cylindrical vessel of diameter d be filled with a liquid so that the total force on the vertical surface of the vessel be equal to the force on the bottom-
View SolutionA solid is completely immersed in a liquid. The force exerted by the liquid on the solid will
View Solution_E01_126_Q01.png)
A massless conical flask filled with a liquid is kepth on t a table in a vacuum the force exerted by the liquid on the bse of the flask is W1. Th force exerted by the flask on the table is W2View SolutionFor the arrangement shown in the figure, the force at the bottom of the vessel is
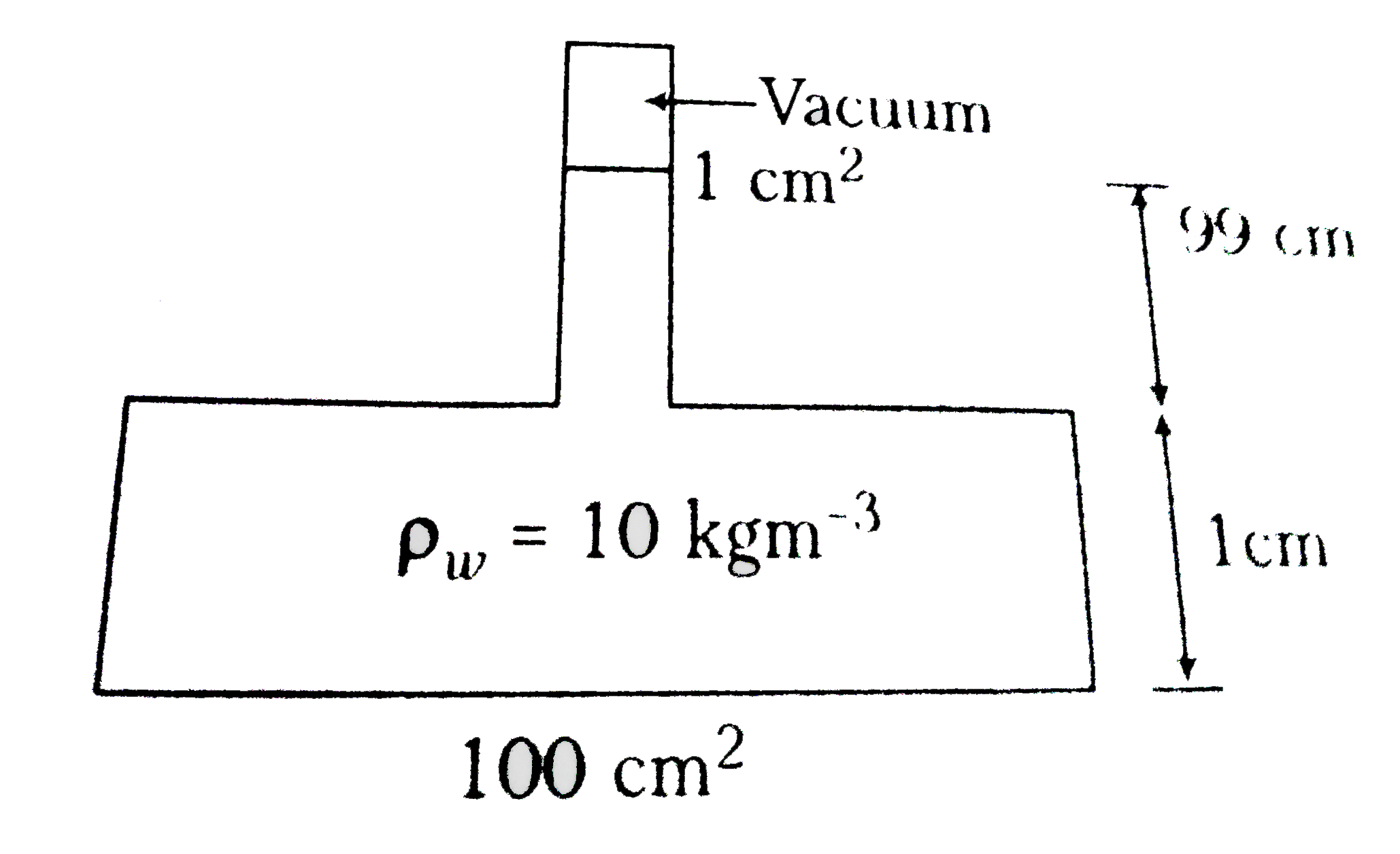 View Solution
View SolutionIn the following figure shown, a liquid is filled into the vessel up to a height h and the forces exerted against the liquid by the walls of the vessel are shown by arrows, the force being everywhere perpendicular to the walls of the vessel. For this situation mark out the correct statement(s).
 View Solution
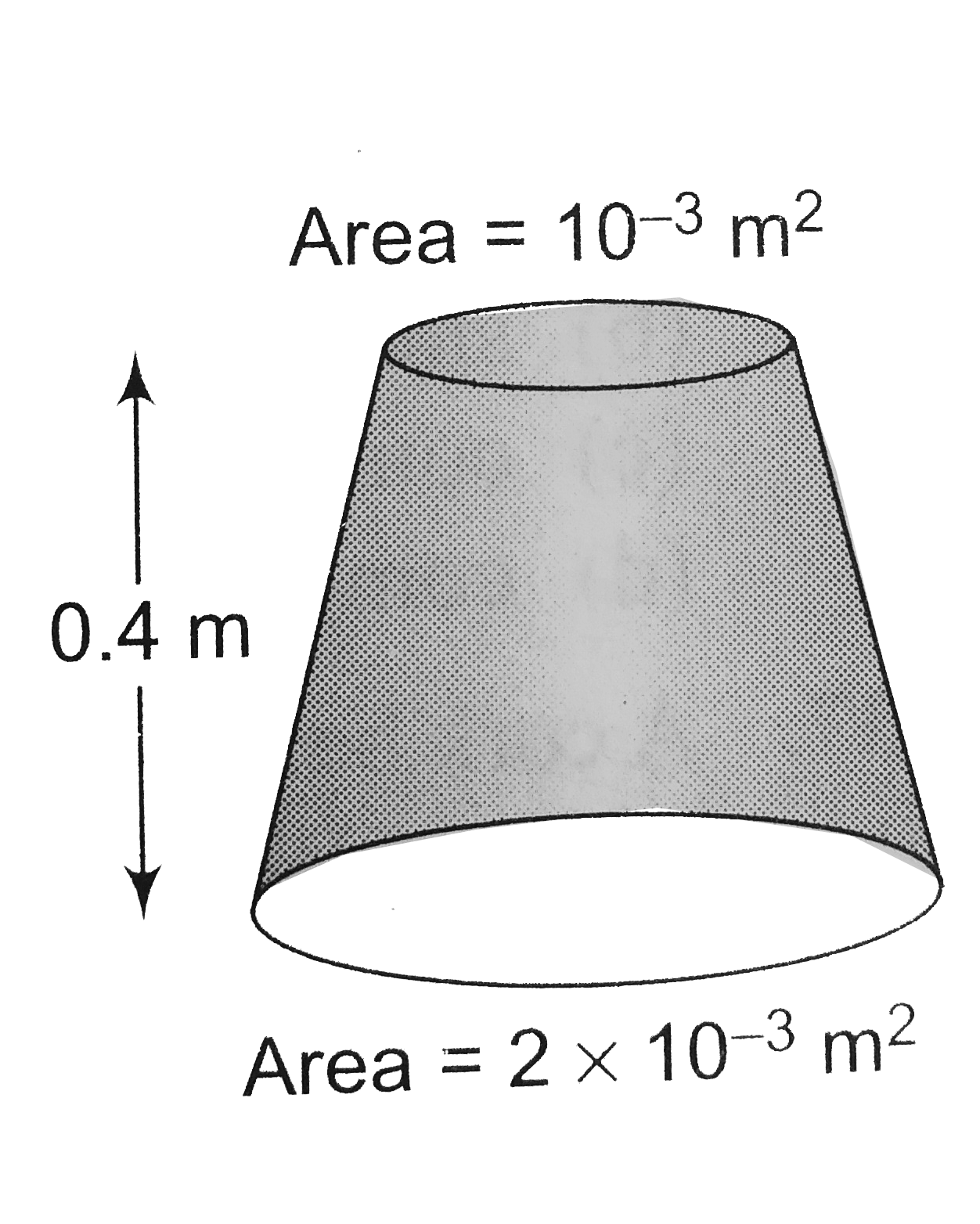
View SolutionA uniformly tapering vessel is filled with a liquid of density 900km/m3. The force that acts on the base of the vessel due to the liquid is (g=10ms−2)
 View Solution
View SolutionThe direction of the force exerted on a surface by a liquid at rest is
View SolutionSome liquid is filled in a cylindrical vessel of radius R. Let F1 be the force applied by the liquid on the bottom of the cylinder. Now the same liquid is poured into a vessel of uniform square cross-section of side R. Let F2 be the force applied by the liquid on the bottom of this new vessel. (Neglect atmosphere pressure). Then
View SolutionA cylindrical vessel is filled with a liquid up to a height H. A small hole is made in the vessel at a distance y below the liquid surface as shown in figure. The liquid emerging from the hole strike the ground at distance x
 View Solution
View SolutionA person just observes the point A on the circumference at the bottom of an empty cylindricla vessel of diameter 10 cm . When the vessel is completely filled with a liquid (μ=√2), he can just see the centre B of the bottom. Then the height of the vessel is
 View Solution
View Solution

