Some liquid is filled in a cylindrical vessel of radius R. Let F1 be the force applied by the liquid on the bottom of the cylinder. Now the same liquid is poured into a vessel of uniform square cross-section of side R. Let F2 be the force applied by the liquid on the bottom of this new vessel. (Neglect atmosphere pressure). Then
F1=πF2
F1=F2π
F1=√πF2
F1=F2
The correct Answer is:D
To solve the problem, we need to analyze the forces exerted by the liquid in both vessels.
1. Identify the Force on the Bottom of the Cylinder (F1):
- The force exerted by the liquid on the bottom of the cylindrical vessel is equal to the weight of the liquid in the cylinder.
- The weight of the liquid can be calculated using the formula:
F1=Weight of liquid=Volume of liquid×Density of liquid×g
- The volume of the liquid in a cylindrical vessel is given by:
V=πR2h
where h is the height of the liquid.
2. Identify the Force on the Bottom of the Square Vessel (F2):
- Similarly, the force exerted by the liquid on the bottom of the square vessel is also equal to the weight of the liquid.
- The volume of the liquid in the square vessel is given by:
V=R2h
- Thus, the force on the bottom of the square vessel can be expressed as:
F2=Weight of liquid=Volume of liquid×Density of liquid×g=R2h×ρ×g
3. Equate the Forces (F1 and F2):
- Since the same amount of liquid is poured into both vessels, the volume of liquid remains constant. Therefore, the weight of the liquid in both cases is the same.
- This means:
F1=F2
4. Conclusion:
- Since F1 is equal to F2, we conclude that:
F1=F2
Final Answer:
Thus, the force applied by the liquid on the bottom of the cylindrical vessel is equal to the force applied by the liquid on the bottom of the square vessel:
F1=F2
- The force exerted by the liquid on the bottom of the cylindrical vessel is equal to the weight of the liquid in the cylinder.
- The weight of the liquid can be calculated using the formula:
F1=Weight of liquid=Volume of liquid×Density of liquid×g
- The volume of the liquid in a cylindrical vessel is given by:
V=πR2h
where h is the height of the liquid.
- Similarly, the force exerted by the liquid on the bottom of the square vessel is also equal to the weight of the liquid.
- The volume of the liquid in the square vessel is given by:
V=R2h
- Thus, the force on the bottom of the square vessel can be expressed as:
F2=Weight of liquid=Volume of liquid×Density of liquid×g=R2h×ρ×g
- Since the same amount of liquid is poured into both vessels, the volume of liquid remains constant. Therefore, the weight of the liquid in both cases is the same.
- This means:
F1=F2
- Since F1 is equal to F2, we conclude that:
F1=F2
Thus, the force applied by the liquid on the bottom of the cylindrical vessel is equal to the force applied by the liquid on the bottom of the square vessel:
F1=F2
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct
21 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Comprehension
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
Similar Questions
To what height h should a cylindrical vessel of diameter d be filled with a liquid so that the total force on the vertical surface of the vessel be equal to the force on the bottom-
View SolutionThe opening near the bottom of the vessel shown in the figure has an area A. A disc is held against the opening keep the liquid from running out. Let F1 be the net forces on the disc applied by liquid and air in this case. Now the disc is moved away from the opening a short distance. The liquid comes out and strikes the disc in elastically. Let F2 be the force exerted by the liquid in this condition. The F1/F2 is

View Solution
Knowledge Check
To what height should a cyclindrical vessel be filled with a homogeneous liquid to make the force with which the liquid pressure on the sides of the vessel equal to the force exerted by the liquid on the bottom of the vessel ?
Aequal to the radiusBless than radiusCmore than radiusDfour times of radius
A liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides. If the radius of the vessel is r and the speed of revolution is n rotations/second, find the difference in height of the liquid at the centre of vessel and its sides.
View SolutionA vessel in the form of a truncated cone has base area a1 and top area a2. It is filled to the brim with a liquid. The force at the bottom of the vessel is
View SolutionThe vessel shown in the figure has two sections of areas of cross-section A1andA2. A liquid of density ρ fills both the section, up to a height h in each. Neglect atmospheric pressure. Choose correct options.
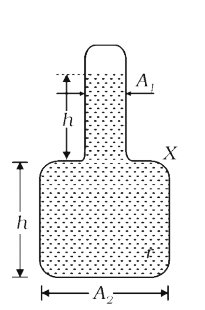
View SolutionA cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is

View SolutionA cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is

View SolutionThe vessel shown in the figure has a two sections of areas of cross-section A1 and A2. A liquid of density ρ fills both th sections, up to a height h in each Neglect atmospheric pressure. Choose the wrong option.
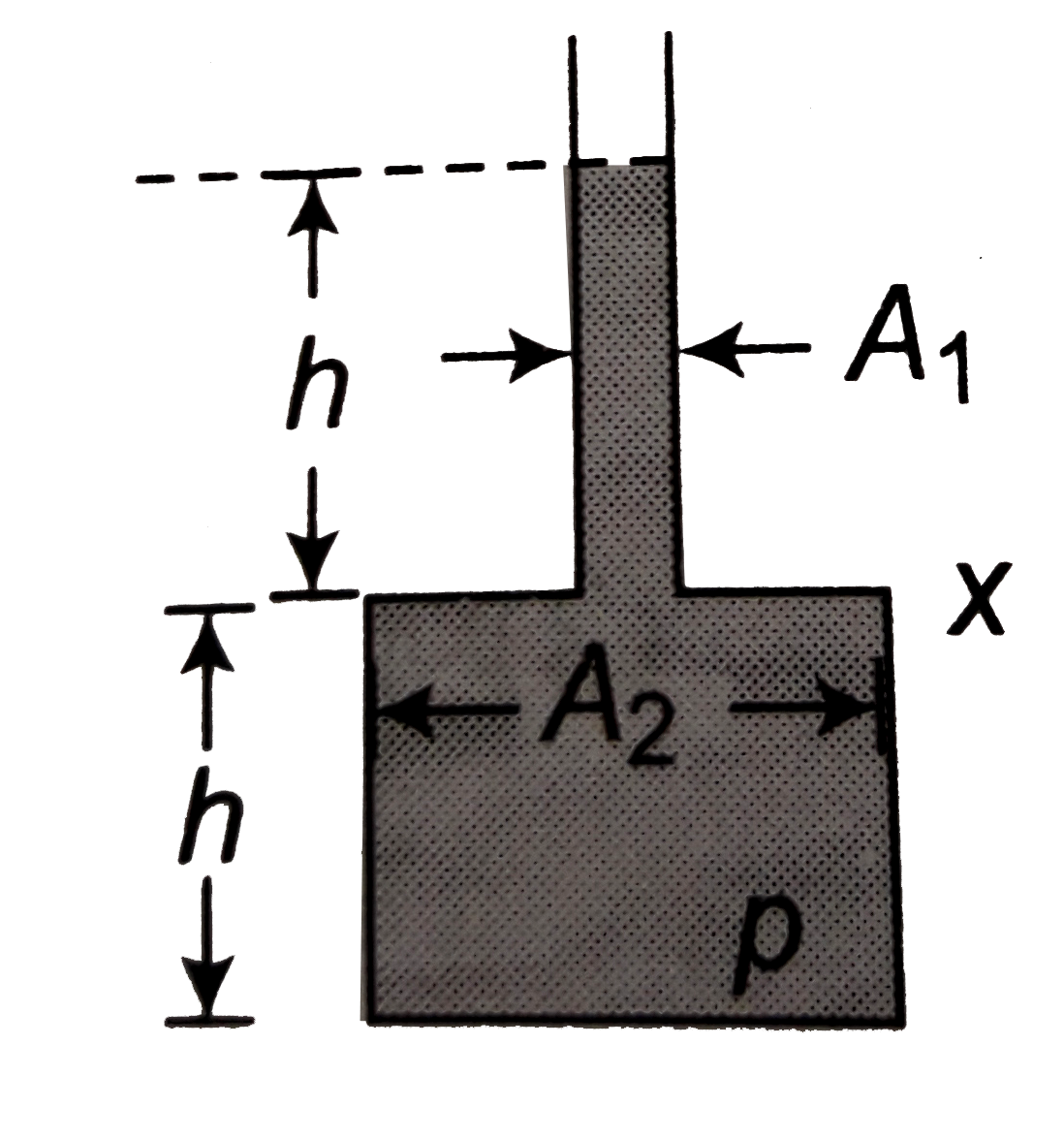 .
.
View SolutionTwo liquid columns of same height 5m and densities ρ and 2ρ are filled in a container of uniform cross sectional area. Then ratio of force exerted by the liquid on upper half of the wall to lower half of the wall is.
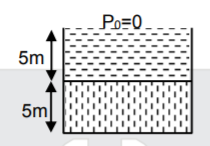
View Solution
