To what height h should a cylindrical vessel of diameter d be filled with a liquid so that the total force on the vertical surface of the vessel be equal to the force on the bottom-
h=d
h=2d
h=3d
h=d/2
The correct Answer is:D
To solve the problem of determining the height h to which a cylindrical vessel of diameter d should be filled with liquid so that the total force on the vertical surface of the vessel equals the force on the bottom, we can follow these steps:
Step 1: Calculate the Force on the Bottom of the Cylinder
The force exerted at the bottom of the cylinder can be calculated using the formula:
Fbottom=P⋅A
where P is the pressure at the bottom and A is the area of the bottom.
The pressure at the bottom of the cylinder is given by:
P=ρgh
where ρ is the density of the liquid, g is the acceleration due to gravity, and h is the height of the liquid.
The area A of the bottom of the cylindrical vessel is:
A=πr2=π(d2)2=πd24
Thus, the force on the bottom is:
Fbottom=ρgh⋅πd24
Step 2: Calculate the Force on the Vertical Surface of the Cylinder
The force exerted by the liquid on the vertical surface of the cylinder can be found by integrating the pressure over the height of the liquid. The pressure at a height y is:
P(y)=ρgy
The differential force dF on a differential area dA at height y is:
dF=P(y)⋅dA=ρgy⋅dA
The differential area dA of the vertical surface at height y is:
dA=2πrdy=2π(d2)dy=πddy
Thus, the total force on the vertical surface from height 0 to h is:
Fvertical=∫h0ρgy⋅πddy
Calculating this integral:
Fvertical=ρgπd∫h0ydy=ρgπd(y22)h0=ρgπd⋅h22
Step 3: Set the Forces Equal
To find the height h such that the total force on the vertical surface equals the force on the bottom, we set:
Fbottom=Fvertical
Substituting the expressions we derived:
ρgh⋅πd24=ρgπd⋅h22
Step 4: Simplify and Solve for h
Canceling ρg and π from both sides:
hd24=h2d2
Rearranging gives:
hd2=2h2
Dividing both sides by h (assuming h≠0):
d2=2h
Thus, we find:
h=d22
Conclusion
The height h to which the cylindrical vessel should be filled is:
h=d2
The force exerted at the bottom of the cylinder can be calculated using the formula:
Fbottom=P⋅A
where P is the pressure at the bottom and A is the area of the bottom.
P=ρgh
where ρ is the density of the liquid, g is the acceleration due to gravity, and h is the height of the liquid.
A=πr2=π(d2)2=πd24
Fbottom=ρgh⋅πd24
The force exerted by the liquid on the vertical surface of the cylinder can be found by integrating the pressure over the height of the liquid. The pressure at a height y is:
P(y)=ρgy
The differential force dF on a differential area dA at height y is:
dF=P(y)⋅dA=ρgy⋅dA
The differential area dA of the vertical surface at height y is:
dA=2πrdy=2π(d2)dy=πddy
Fvertical=∫h0ρgy⋅πddy
Calculating this integral:
Fvertical=ρgπd∫h0ydy=ρgπd(y22)h0=ρgπd⋅h22
To find the height h such that the total force on the vertical surface equals the force on the bottom, we set:
Fbottom=Fvertical
Substituting the expressions we derived:
ρgh⋅πd24=ρgπd⋅h22
Canceling ρg and π from both sides:
hd24=h2d2
Rearranging gives:
hd2=2h2
Dividing both sides by h (assuming h≠0):
d2=2h
Thus, we find:
h=d22
The height h to which the cylindrical vessel should be filled is:
h=d2
Topper's Solved these Questions
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 2 (One or more than one correct answer)
53 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 3 (Assertion & Reason)
32 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Surface Tension)
21 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
Similar Questions
Two identical cylindrical vessels have the same base area but are filled with different volumes of water . The forces on the bases of the two vessels are same ?
View SolutionIf water is ejecting from a hole of radius r at a depth h from the water surface in cylindrical vessel of diameter D, then speed with which the water level in the vessel drops .(Consider area of hole is comparable to area of vessel)
View Solution
Knowledge Check
To what height should a cyclindrical vessel be filled with a homogeneous liquid to make the force with which the liquid pressure on the sides of the vessel equal to the force exerted by the liquid on the bottom of the vessel ?
Aequal to the radiusBless than radiusCmore than radiusDfour times of radius
A person just observes the point A on the circumference at the bottom of an empty cylindricla vessel of diameter 10 cm . When the vessel is completely filled with a liquid (μ=√2), he can just see the centre B of the bottom. Then the height of the vessel is

View SolutionIf for a liquid in a vessel force of cohesion is twice of adhesion
View SolutionA sphere just fits in a cylindrical vessel and the height of the cylindrical vessel is the same as the height of the spere . Show that the curved surface area of the cylinder is the same as the curved surface area of the sphere .
View SolutionA uniformly tapering vessel is filled with a liquid of density 900km/m3. The force that acts on the base of the vessel due to the liquid is (g=10ms−2)
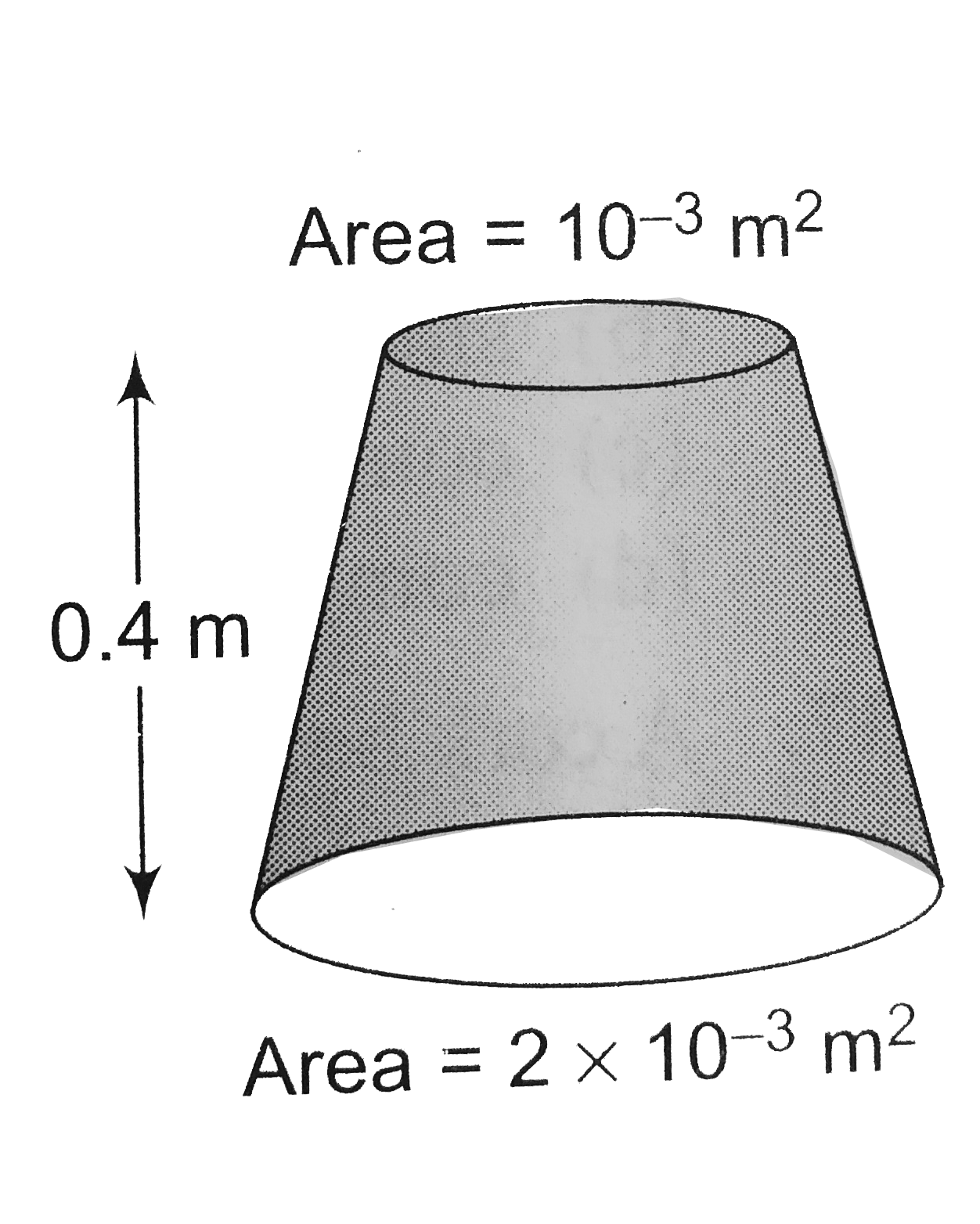
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the side. If the radius of the vessel is 5cm and the speed of rotation is 4rev/s, then the difference in the height of the liquid at the centre of the vessel and its sides is
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides. If the radius of the vessel is r and the speed of revolution is n rotations/second, find the difference in height of the liquid at the centre of vessel and its sides.
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the side. If the radius of the vessel is 5cm and the speed of rotation is 4rev/s, then the difference in the height of the liquid at the centre of the vessel and its sides is
View Solution
