An ideal flow of any fluid must satisfy
1. Pascal law
2. Stokes' law
3. Continuity equation
4. Bernoulli's theorem
The correct Answer is:C
To determine what an ideal flow of any fluid must satisfy, we need to analyze the definitions and implications of the terms involved.
1. Understanding Ideal Flow:
- An ideal flow refers to the flow of an incompressible fluid that flows steadily without any friction. This means that the viscosity (η) of the fluid is considered to be zero.
2. Evaluating the Options:
- Pascal's Law:
- This law states that a pressure change at any point in a static fluid is transmitted undiminished throughout the fluid. Since ideal flow refers to dynamic conditions (not static), Pascal's law does not apply here.
- Stokes' Law:
- Stokes' law describes the drag force experienced by a sphere moving through a viscous fluid. Since ideal flow assumes zero viscosity, Stokes' law is also not applicable.
- Continuity Equation:
- The continuity equation arises from the conservation of mass principle. It states that the mass flow rate must remain constant in a fluid flow. This equation is valid for both ideal and real fluids, making it applicable to ideal flow.
- Bernoulli's Theorem:
- Bernoulli's theorem relates to the conservation of energy in fluid flow. It applies to laminar flow conditions, which typically involve some viscosity. Therefore, it is not applicable to ideal flow where viscosity is zero.
3. Conclusion:
- The only option that satisfies the conditions of an ideal flow is the continuity equation.
Thus, the correct answer is the continuity equation.
- An ideal flow refers to the flow of an incompressible fluid that flows steadily without any friction. This means that the viscosity (η) of the fluid is considered to be zero.
- Pascal's Law:
- This law states that a pressure change at any point in a static fluid is transmitted undiminished throughout the fluid. Since ideal flow refers to dynamic conditions (not static), Pascal's law does not apply here.
- Stokes' Law:
- Stokes' law describes the drag force experienced by a sphere moving through a viscous fluid. Since ideal flow assumes zero viscosity, Stokes' law is also not applicable.
- Continuity Equation:
- The continuity equation arises from the conservation of mass principle. It states that the mass flow rate must remain constant in a fluid flow. This equation is valid for both ideal and real fluids, making it applicable to ideal flow.
- Bernoulli's Theorem:
- Bernoulli's theorem relates to the conservation of energy in fluid flow. It applies to laminar flow conditions, which typically involve some viscosity. Therefore, it is not applicable to ideal flow where viscosity is zero.
- The only option that satisfies the conditions of an ideal flow is the continuity equation.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Higher Order Thinking Skills
8 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Exemplar Problems
5 Videos
- LAWS OF MOTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assertion And Reason
15 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
For total internal reflection to take place, the angle of incidence i and the refractive index μ of the medium must satisfy the inequality
View SolutionAn object is moving towards a converging lens on its axis. The image is also found to be moving towards the lens. Then, the object distance u must satisfy
View Solution
Knowledge Check
Assertion: The flow of fluid is said to be steady if at any given point, the velocity of each passing fluid particle remains constant.
Reason: The path taken by a fluid particle under a steady flow is a streamline.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true and reason is false.DIf both assertion and reason are false.
Assertion: The velocity of flow of a liquid is smaller when pressure is larger and vice versa.
Reason: According to Bernoulli's theorem, for the stream line flow of an ideal liquid, the total energy per unit mass remains constant.
View SolutionWhat is a fluid ?
View SolutionA fluid comparises of
View SolutionIn the given circuit, it is observed that the current I is independent of the value of the resistance R6. Then the resistance values must satisfy
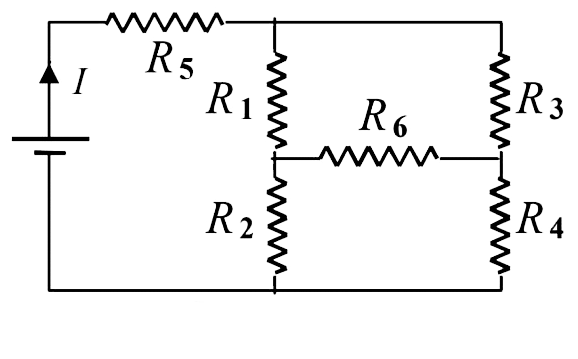 .
.
View SolutionIn the given circuit, it is observed that the current I is independent of the value of the resistance R6. Then the resistance values must satisfy
 .
.
View SolutionFor a stream line flow of water following statements are given below
(a) Two streamlines do not intersect each other.
(b) streamlines must be straight.
(c) streamlines flow is more likely for liquids with low density and height viscosity.
(d) streamlines flow is more likely for liquids with high density and low viscosity.
View SolutionFluid Flows
View Solution
