For total internal reflection to take place, the angle of incidence i and the refractive index μ of the medium must satisfy the inequality
μ=sinc
μ=tanc
(1μ)=sinc
(1μ)=cosc
The correct Answer is:C
To determine the conditions for total internal reflection to occur, we need to analyze the relationship between the angle of incidence (i) and the refractive index (µ) of the medium. Here’s a step-by-step solution:
Step 1: Understand Total Internal Reflection
Total internal reflection occurs when light travels from a denser medium to a rarer medium and the angle of incidence exceeds a certain critical angle (C).
Step 2: Define Critical Angle
The critical angle (C) is defined as the angle of incidence in the denser medium at which the angle of refraction in the rarer medium is 90 degrees.
Step 3: Apply Snell's Law
Using Snell's Law, which states:
μsin(i)=μ1sin(r)
where:
- μ is the refractive index of the denser medium,
- μ1 is the refractive index of the rarer medium (for air, it is approximately 1),
- i is the angle of incidence,
- r is the angle of refraction.
Step 4: Set Up the Equation for Critical Angle
At the critical angle (C), the angle of refraction (r) is 90 degrees. Therefore, we can substitute r=90∘ into Snell's Law:
μsin(C)=μ1sin(90∘)
Since sin(90∘)=1, this simplifies to:
μsin(C)=μ1
Step 5: Solve for the Critical Angle
Rearranging the equation gives us:
sin(C)=μ1μ
For air, where μ1=1:
sin(C)=1μ
Step 6: Establish the Condition for Total Internal Reflection
For total internal reflection to occur, the angle of incidence (i) must be greater than the critical angle (C):
i>C
This means:
i>sin−1(1μ)
Final Conclusion
Thus, the inequality that must be satisfied for total internal reflection to take place is:
i>sin−1(1μ)
Total internal reflection occurs when light travels from a denser medium to a rarer medium and the angle of incidence exceeds a certain critical angle (C).
The critical angle (C) is defined as the angle of incidence in the denser medium at which the angle of refraction in the rarer medium is 90 degrees.
Using Snell's Law, which states:
μsin(i)=μ1sin(r)
where:
- μ is the refractive index of the denser medium,
- μ1 is the refractive index of the rarer medium (for air, it is approximately 1),
- i is the angle of incidence,
- r is the angle of refraction.
At the critical angle (C), the angle of refraction (r) is 90 degrees. Therefore, we can substitute r=90∘ into Snell's Law:
μsin(C)=μ1sin(90∘)
Since sin(90∘)=1, this simplifies to:
μsin(C)=μ1
Rearranging the equation gives us:
sin(C)=μ1μ
For air, where μ1=1:
sin(C)=1μ
For total internal reflection to occur, the angle of incidence (i) must be greater than the critical angle (C):
i>C
This means:
i>sin−1(1μ)
Thus, the inequality that must be satisfied for total internal reflection to take place is:
i>sin−1(1μ)
Topper's Solved these Questions
Similar Questions
Under what conditions is the phenomenon of total internal reflection between the critical angle of incidence and the refractive index of the medium.
View SolutionIn total internal reflection when the angle of incidence is equal to the critical angle for the pair of medium in contact, what will be angle of refraction? In total internal reflection when the angle of incidence is equal to the critical angle for the pair of medium in contact, what will be angle of refraction? In total internal reflection when the angle of incidence is equal to the critical angle for the pair of medium in contact, what will be angle of refraction?
View Solution
Knowledge Check
Select correct options for Total internal reflection in a medium.
Can take place in an optically denser medium as compared to an optically rarer medium.
Takes place for any angle of incidence greater than 42 degree.
This reflection does not obey the laws of reflection.
Can take place if the angle of incidence in a denser medium is more than the critical angle.ACan take place in an optically denser medium as compared to an optically rarer medium.BTakes place for any angle of incidence greater than 42 degree.CThis reflection does not obey the laws of reflection.DCan take place if the angle of incidence in a denser medium is more than the critical angle.
Light travelling through three transparent substances follows the path shown in the figure. Assuming that total internal reflection does take place on the bottom surface of medium 2, arrange the refractive index in the increasing order.

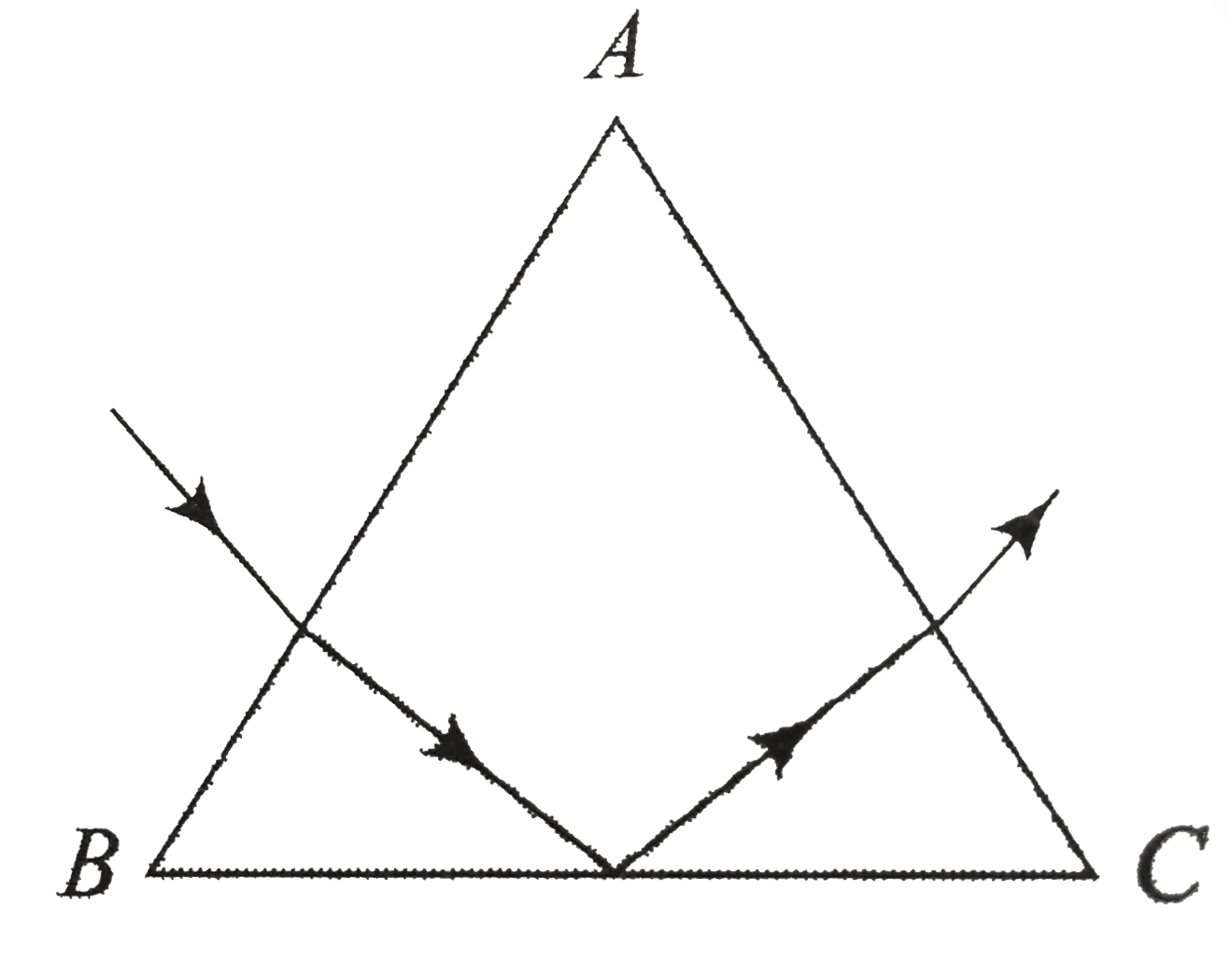
View SolutionThe path of a ray of light passing through an equilateral glass prism ABC is shown in figure. The ray of light is incident on face BC at the critical angle for just total internal reflection. The total internal reflection. The total angle of deviation after the refraction at face AC is 108∘. Calculate the refractive index of the glass.
View SolutionA ray of light travelling in a transparent medium falls on a surface separating the medium from air at an angle of incidence of 45∘. The ray undergoes total internal reflection. If n is the refractive index of the medium with respect to air, select the possible value of n from the following.
View SolutionFor a given incident ray as shown in Fig., the condition of total internal reflection of ray will be satisfied if the refractive index of the block will be.
 .
.
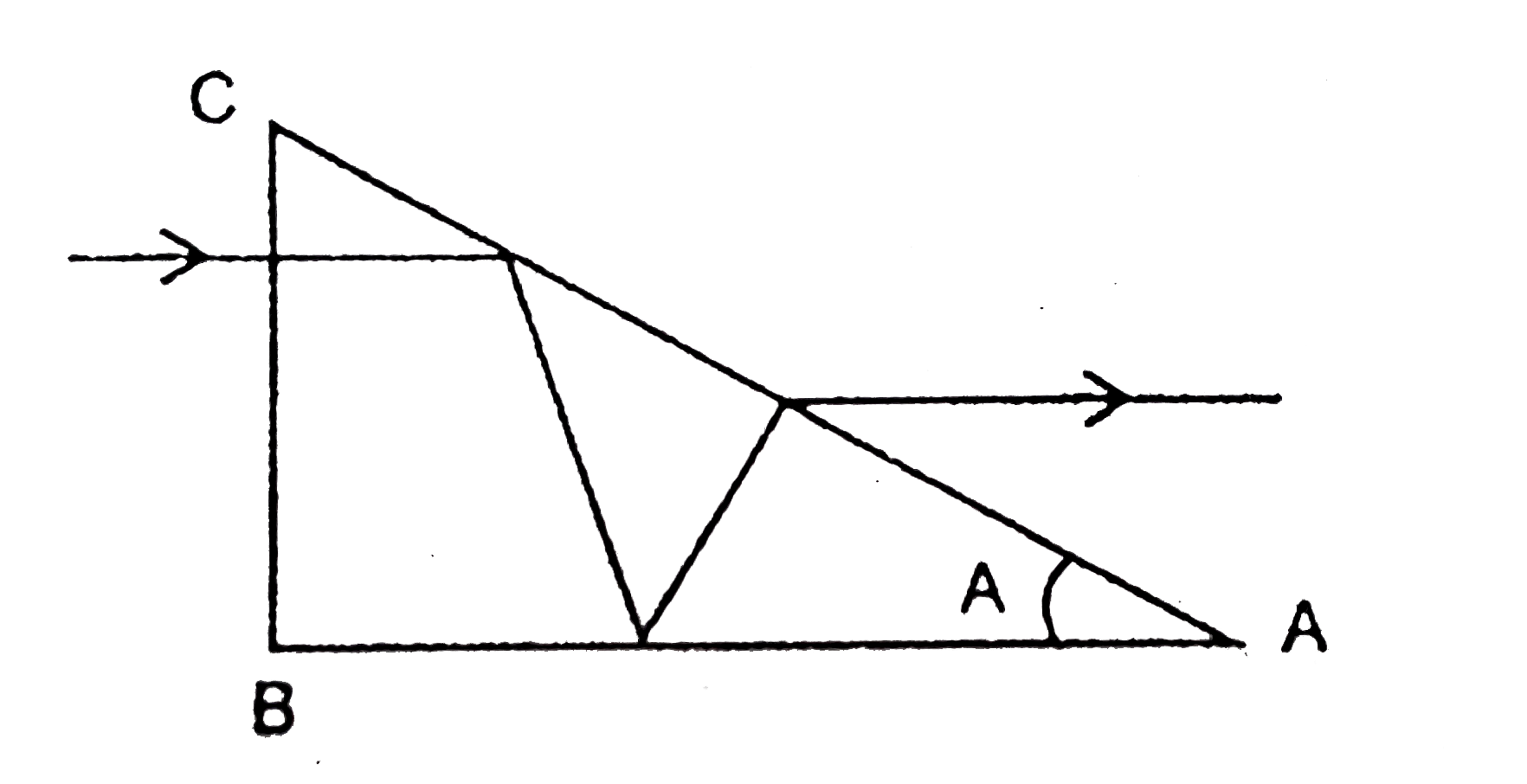
View SolutionA ray of light falls normally on one face of a right angled prims of refracting angle A. It suffers two total internal reflections before coming out of prism parallel to incident ray as shown. Refractive index to prism material will be:
View SolutionA light ray is incident perpendicularly to one face of a 90∘ prism and is totally internally reflected at the glass-air interface. If the angle of reflection is 45∘, we conclude that the refractive index n

View SolutionA ray of light is incident from a denser to a rarer medium. The critical angle for total internal reflection is θic and Brewster's angle of incidence is θiB such that sinθicsinθiB=η=1.28 . The relative refractive index of the two media is
View Solution