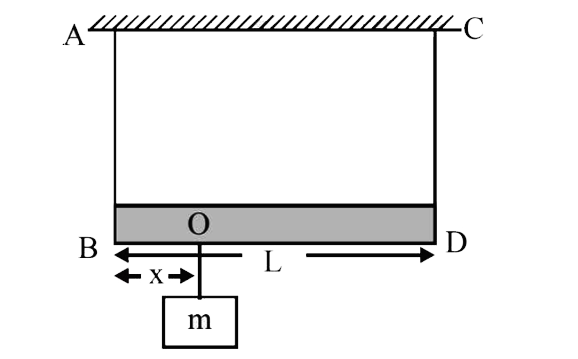
A massless rod of length L is suspened by two identical string AB and CD of equal length. A block of mass m is suspended from point O such that BO is equal to 'x'. Further it is observed that the frequency of 1st harmonic in AB is equal to 2nd harmonic frequency in CD. 'x' is
L5
4L5
3L4
L4
The correct Answer is:A
Frequency of the first harmonic of AB
=12l√TABm, When l is the length of the two strings.
Frequency of the 2nd harmonic of CD
=1l√TCDm
Given that the two frequencies are equal.
∴ 12l√TABm=1l√TCDm⇒TAB4=TCD
⇒ TAB=4TCD ...(ii)
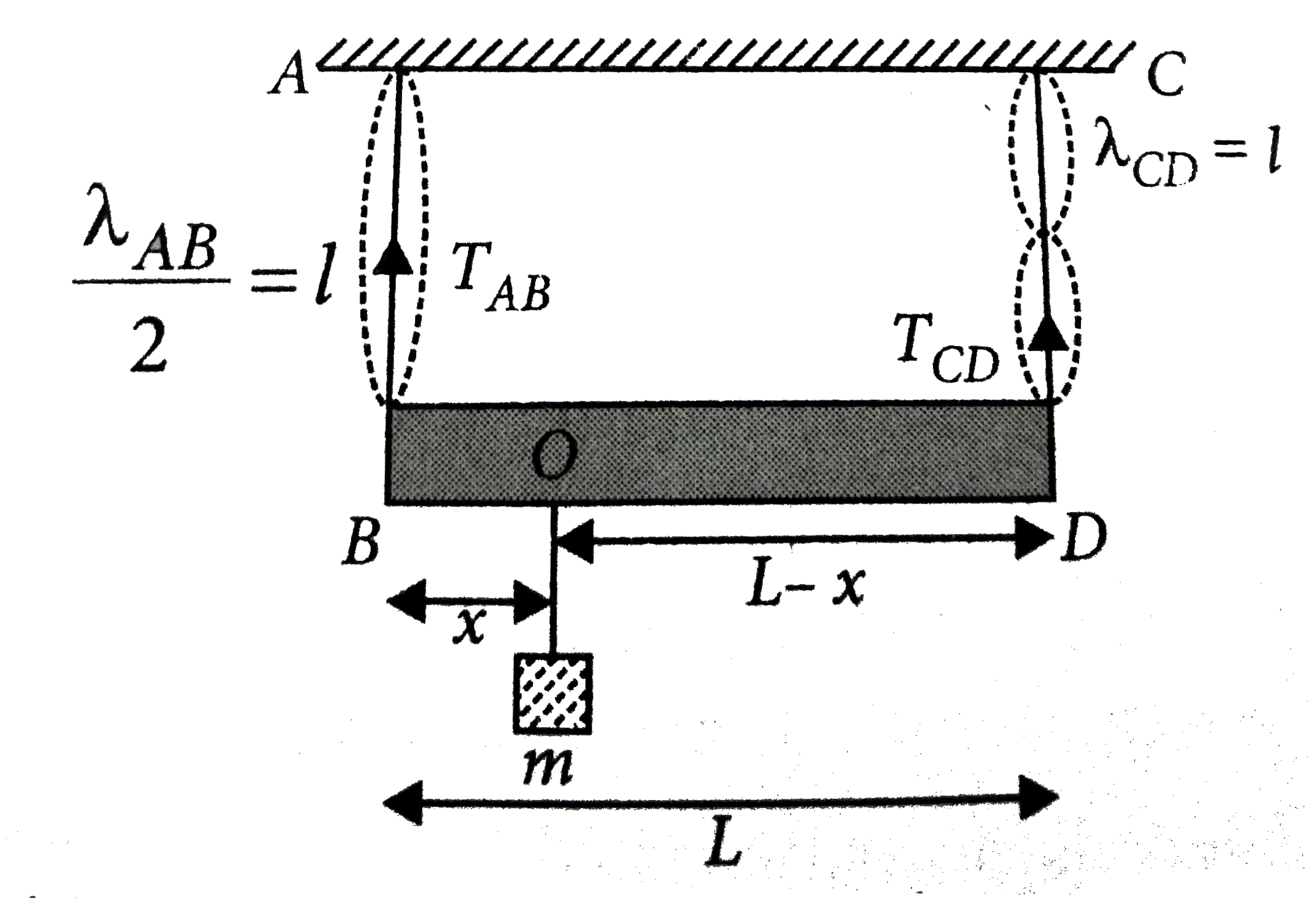
For rotation equilibrium of masscles rod taking torque about point O.
TAB×x=TCD(L−x) ...(iii)
Solve to get, x=L5
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVESEXERCISE - EXEMPLER10videos
WAVES
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVESEXERCISE - ASSERTION15videos
WAVES
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVESEXERCISE - Assertion And Reason15videos
WAVES
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - Assertion And Reason15videos
UNITS AND MEASUREMENTS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WORK , ENERGY AND POWEREXERCISE - Assertion And Reason15videos
WORK , ENERGY AND POWER
Similar Questions
A massless rod BD is suspended by two identical massless strings AB and CD of equal lengths. A block of mass m is suspended at point P such that BP is equal to x, If the fundamental frequency of the left wire is twice the fundamental frequency of right wire, then the value of x is :-
_E01_188_Q01.png) View Solution
View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O
 View Solution
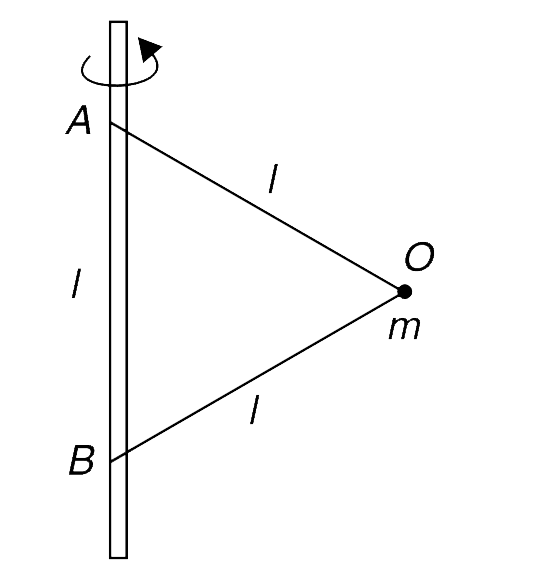
View SolutionA particle of mass m is attached to a vertical rod with two inextensible strings AO and BO of equal lengths l. Distance between A and B is also l. The setup is rotated with angular speed ω with rod as the axis.
 View Solution
View SolutionA rod of length L is composed of a uniform length 1/2 L of wood mass is mw and a uniform length 1/2 L of brass whose mass is mb. The moment of inertia I of the rod about an axis perpendicular to the rod and through its centre is equal to
View Solution
A uniform rod AB is suspended from a point X, at a variable distance x from A, as shown. To make the rod horizontal , a mass m is suspended from its end A. A set of (m,x) value is recorded that give a straight line, when plotted, are :View SolutionA point mass m is suspended at the end of a massless wire of length l and cross section. If Y is the Young's modulus for the wire, obtain the frequency of oscillation for the simple harmonic motion along the vertical line.
View SolutionTwo identical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View SolutionA uniform rod of length l and mass m is hung from, strings of equal length from a ceiling as shown in figure. Determine the tensions in the strings?
 View Solution
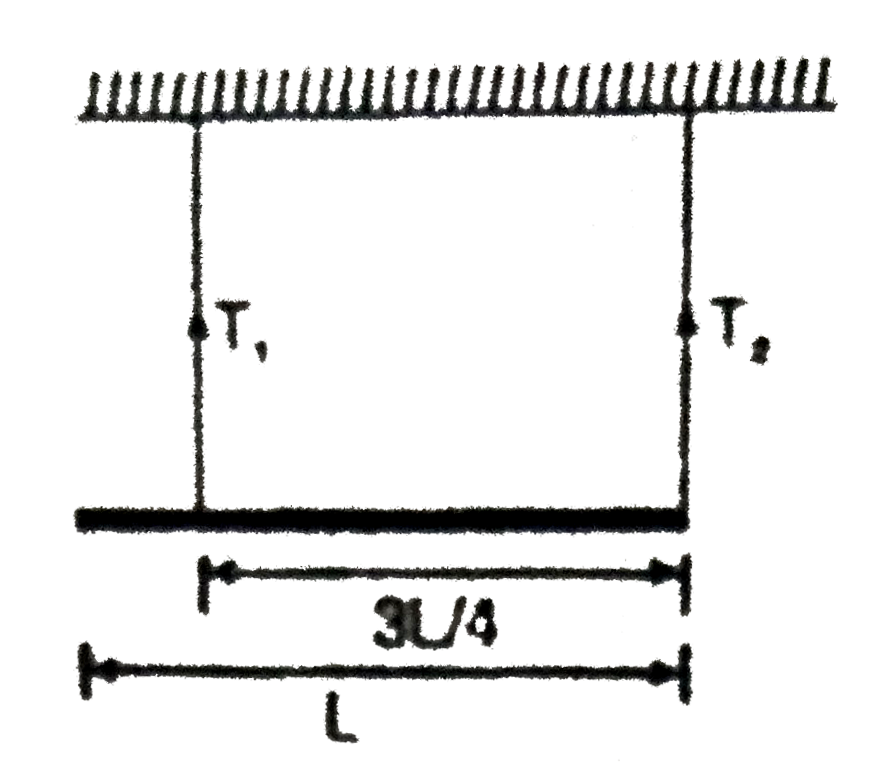
View SolutionA uniform rod of mass m and length L is suspended with two massless strings as shown in the figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings T1T2 is:
 View Solution
View SolutionTwo indentical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View Solution

