For the same total mass, which of the following will have the largest moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of the body a) A disc of radius a b) A ring of radius a c) A square lamina of side a d) Four identical rods forming square of side a
A disc of radius a
A ring of radius a
A square lamina of side a
Four identical rods forming square of side a
The correct Answer is:D
To determine which of the given shapes has the largest moment of inertia about an axis passing through the center of mass and perpendicular to the plane of the body, we will calculate the moment of inertia for each shape.
Step 1: Moment of Inertia of a Disc
For a disc of radius a and mass m, the moment of inertia I about an axis through its center and perpendicular to its plane is given by the formula:
Idisc=12ma2
Step 2: Moment of Inertia of a Ring
For a ring of radius a and mass m, the moment of inertia about an axis through its center and perpendicular to its plane is given by:
Iring=ma2
Step 3: Moment of Inertia of a Square Lamina
For a square lamina of side a and mass m, the moment of inertia about an axis through its center and perpendicular to its plane is given by:
Isquare=16ma2
Step 4: Moment of Inertia of Four Identical Rods Forming a Square
For four identical rods forming a square of side a, the moment of inertia of one rod about its center is 112ma2. Since there are four rods, the total moment of inertia for the square configuration is:
Irods=4×112ma2=13ma2
Step 5: Compare the Moments of Inertia
Now we can summarize the moments of inertia calculated:
- For the disc: Idisc=12ma2
- For the ring: Iring=ma2
- For the square lamina: Isquare=16ma2
- For the four rods: Irods=13ma2
Step 6: Determine the Largest Moment of Inertia
Now we compare the values:
- 12ma2 (disc)
- ma2 (ring)
- 16ma2 (square)
- 13ma2 (four rods)
Clearly, Iring=ma2 is the largest among these values.
Final Answer
Thus, the shape with the largest moment of inertia about an axis passing through the center of mass and perpendicular to the plane of the body is:
Option b) A ring of radius a.
---
For a disc of radius a and mass m, the moment of inertia I about an axis through its center and perpendicular to its plane is given by the formula:
Idisc=12ma2
For a ring of radius a and mass m, the moment of inertia about an axis through its center and perpendicular to its plane is given by:
Iring=ma2
For a square lamina of side a and mass m, the moment of inertia about an axis through its center and perpendicular to its plane is given by:
Isquare=16ma2
For four identical rods forming a square of side a, the moment of inertia of one rod about its center is 112ma2. Since there are four rods, the total moment of inertia for the square configuration is:
Irods=4×112ma2=13ma2
Now we can summarize the moments of inertia calculated:
- For the disc: Idisc=12ma2
- For the ring: Iring=ma2
- For the square lamina: Isquare=16ma2
- For the four rods: Irods=13ma2
Now we compare the values:
- 12ma2 (disc)
- ma2 (ring)
- 16ma2 (square)
- 13ma2 (four rods)
Thus, the shape with the largest moment of inertia about an axis passing through the center of mass and perpendicular to the plane of the body is:
Option b) A ring of radius a.
Topper's Solved these Questions
Similar Questions
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
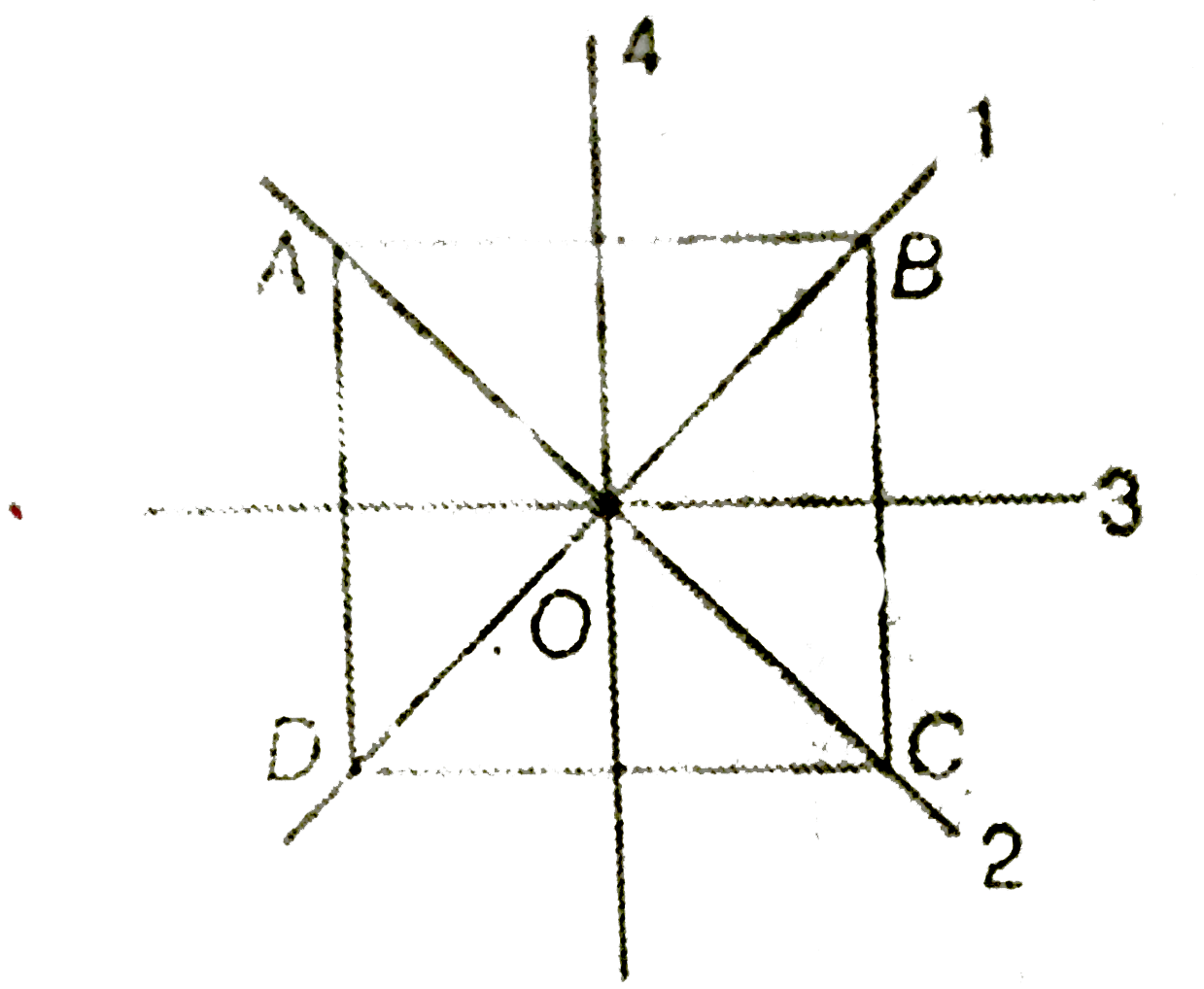
View SolutionThe moment of inertia of a thin square plate ABCD of uniform thickness about an axis passing through the centre O and perpendicular to plate is
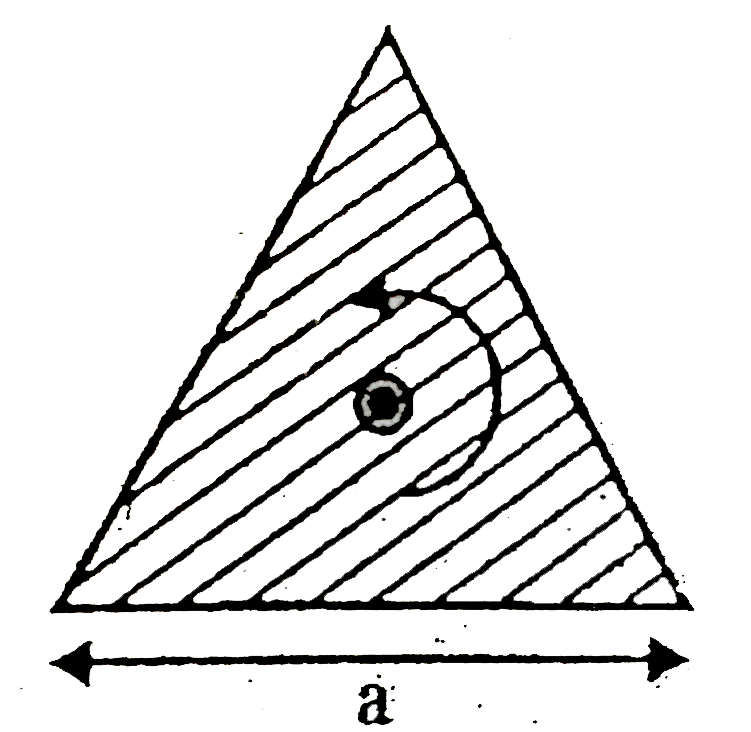
View SolutionA uniform equilateral triangular lamina of side a has mass m. Its moment of inertia about the axis passing through the centroid and prependicular to the plane of the lamina is :-
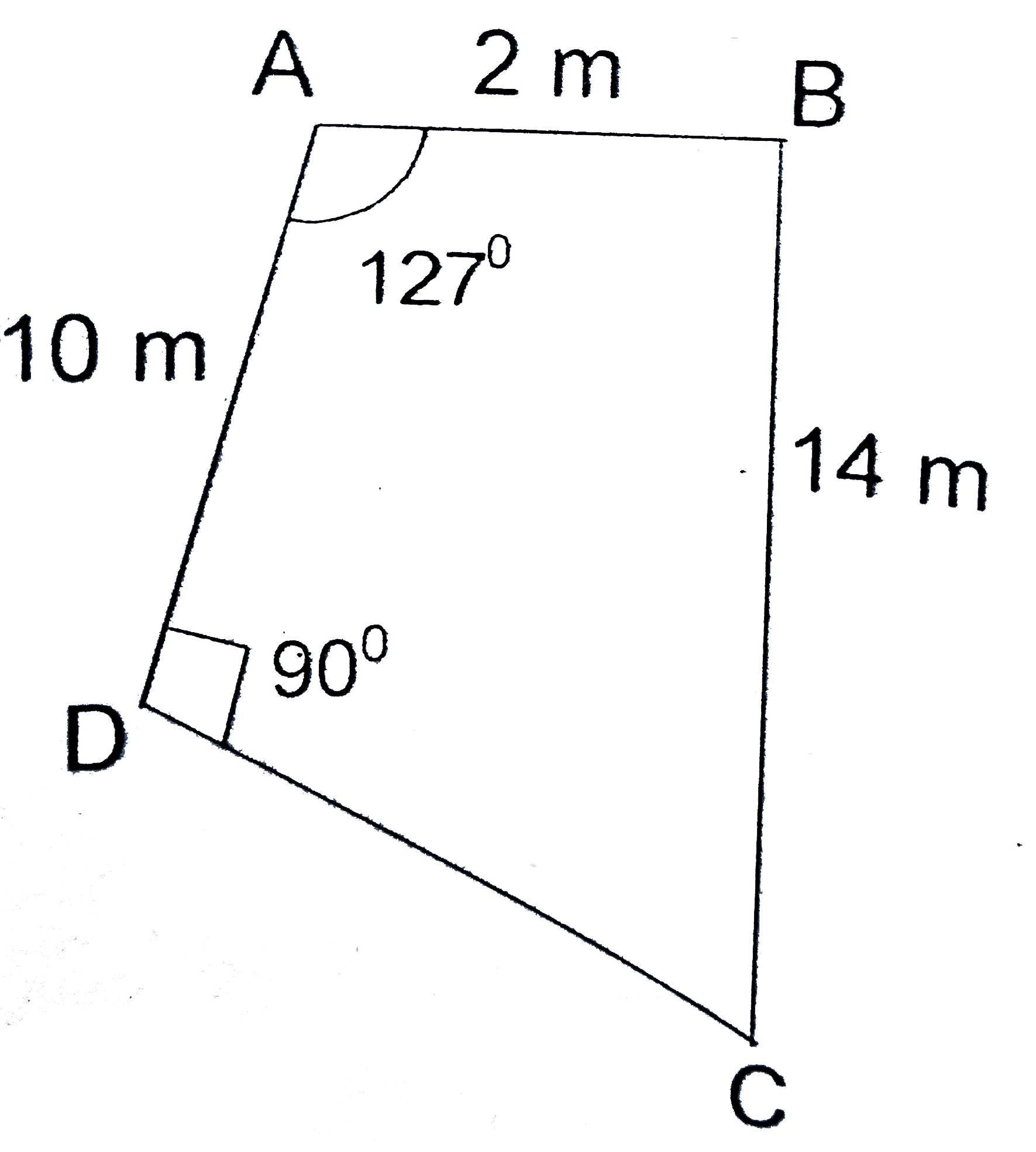
View SolutionIn the figure shown ABCD is a lamina of mass 12kg. The moment of inertia of the given body about an axis passing through D, and perpendicular to the plane of the body is
View SolutionA uniform rod of mass m is bent into the form of a semicircle of radius R. The moment of inertia of the rod about an axis passing through A and perpendicular to the plane of the paper is

View SolutionA uniform rod of mass m is bent into the form of a semicircle of radius R. The moment of inertia of the rod about an axis passing through A and perpendicular to the plane of the paper is

View SolutionThe mass of a disc is 700 gm and its radius of gyration is 20 cm. What is its moment of inertia if it rotates about an axis passing through its centre and perpendicular to the face of the disc?
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View Solution
