A liquid of density ρ0 is filled in a wide tank to a height h. A solid rod of length L, cross-section A and density ρ is suspended freely in the tank. The lower end of the rod touches the base of the tank and h=L/n (where n gt 1). Then the angle of inclination θ of the rod with the horizontal in equilibrium position is
sin−1(√ρ0ρ)
sin−1(n√ρ0ρ)
sin−1(1n√ρ0ρ)
sin−1(1n√ρρ0)
The correct Answer is:C
To solve the problem step by step, we will analyze the forces acting on the rod and use the equilibrium conditions to find the angle of inclination θ.
Step 1: Understand the setup
We have a tank filled with a liquid of density ρ0 to a height h. A solid rod of length L, cross-sectional area A, and density ρ is suspended in the tank such that its lower end touches the base of the tank, and the height of the liquid is given by h=Ln where n>1.
Step 2: Identify the forces acting on the rod
The forces acting on the rod are:
1. The weight of the rod W acting downwards at its center of gravity.
2. The buoyant force FB acting upwards at the center of the submerged part of the rod.
Step 3: Calculate the weight of the rod
The weight W of the rod can be expressed as:
W=ρ⋅A⋅L⋅g
where g is the acceleration due to gravity.
Step 4: Calculate the buoyant force
The buoyant force FB is given by Archimedes' principle:
FB=ρ0⋅A⋅Vimmersed⋅g
The volume of the rod that is immersed in the liquid can be calculated as:
Vimmersed=A⋅h
Given h=Ln, we have:
Vimmersed=A⋅Ln
Thus, the buoyant force becomes:
FB=ρ0⋅A⋅(A⋅Ln)⋅g=ρ0⋅A2⋅Ln⋅g
Step 5: Set up the equilibrium condition
For the rod to be in equilibrium, the sum of torques about any point must be zero. We can choose the lower end of the rod as the pivot point. The torques due to the weight and buoyant force must balance each other.
Let’s denote the length of the rod submerged in the liquid as Limmersed. The center of gravity of the rod is located at L2 from the bottom, and the center of buoyancy is at Limmersed2.
The torque due to the weight W is:
τW=W⋅(L2cosθ)
The torque due to the buoyant force FB is:
τB=FB⋅(Limmersed2cosθ)
Setting the torques equal for equilibrium:
W⋅(L2cosθ)=FB⋅(Limmersed2cosθ)
Step 6: Substitute the expressions for weight and buoyant force
Substituting the expressions for W and FB:
ρ⋅A⋅L⋅g⋅(L2cosθ)=ρ0⋅A2⋅Ln⋅g⋅(Limmersed2cosθ)
Step 7: Cancel common terms and simplify
Canceling g, A, and 12:
ρ⋅L=ρ0⋅Limmersedn
Step 8: Relate Limmersed to L
Since Limmersed=Ln:
ρ⋅L=ρ0⋅Ln2
Step 9: Solve for sinθ
From the geometry of the setup, we can relate sinθ to the height of the liquid:
sinθ=hL=L/nL=1n
Step 10: Final expression for the angle of inclination
Using the relationship derived earlier:
sinθ=1n√ρ0ρ
Thus, the angle of inclination θ is given by:
θ=sin−1(1n√ρ0ρ)
We have a tank filled with a liquid of density ρ0 to a height h. A solid rod of length L, cross-sectional area A, and density ρ is suspended in the tank such that its lower end touches the base of the tank, and the height of the liquid is given by h=Ln where n>1.
The forces acting on the rod are:
1. The weight of the rod W acting downwards at its center of gravity.
2. The buoyant force FB acting upwards at the center of the submerged part of the rod.
The weight W of the rod can be expressed as:
W=ρ⋅A⋅L⋅g
where g is the acceleration due to gravity.
The buoyant force FB is given by Archimedes' principle:
FB=ρ0⋅A⋅Vimmersed⋅g
The volume of the rod that is immersed in the liquid can be calculated as:
Vimmersed=A⋅h
Given h=Ln, we have:
Vimmersed=A⋅Ln
Thus, the buoyant force becomes:
FB=ρ0⋅A⋅(A⋅Ln)⋅g=ρ0⋅A2⋅Ln⋅g
For the rod to be in equilibrium, the sum of torques about any point must be zero. We can choose the lower end of the rod as the pivot point. The torques due to the weight and buoyant force must balance each other.
τW=W⋅(L2cosθ)
The torque due to the buoyant force FB is:
τB=FB⋅(Limmersed2cosθ)
W⋅(L2cosθ)=FB⋅(Limmersed2cosθ)
Substituting the expressions for W and FB:
ρ⋅A⋅L⋅g⋅(L2cosθ)=ρ0⋅A2⋅Ln⋅g⋅(Limmersed2cosθ)
Canceling g, A, and 12:
ρ⋅L=ρ0⋅Limmersedn
Since Limmersed=Ln:
ρ⋅L=ρ0⋅Ln2
From the geometry of the setup, we can relate sinθ to the height of the liquid:
sinθ=hL=L/nL=1n
Using the relationship derived earlier:
sinθ=1n√ρ0ρ
Thus, the angle of inclination θ is given by:
θ=sin−1(1n√ρ0ρ)
Topper's Solved these Questions
Similar Questions
The density of a rod of length L varies as ρ=A+Bx where x is the distance from the left end. Locate the centre of mass.
 View Solution
View SolutionTwo non-mixing liquids of densities ρ and nρ (n>1) are put in a container. The height of each liquid is h. A solid cylinder of length L and density d is put in this container. The cylinder floats with its axis vertical and length pL(p<1) in the denser liquid. The density d is equal to :
View SolutionTwo immiscible liquid of densities rho and 3ρ are put in a container. The height of each liquid is h. A solid cylinder of length L and density d is put in this container. The cylinder floats completely inside liquids with its axis vertical and length L3 in the denser liquid. The density d is equal to
View SolutionA rod of length L and cross section area A has variable density according to the relation ρ(x)=ρ0+kx for 0≤x≤L2 and ρ(x)=2x2 for L2≤x≤L where ρ0 and k are constants. Find the mass of the rod.
View SolutionA liquid of density ρ is filled in a U-tube is accelerated with an acceleration a so that the height of liquid in its two vertical arms are h1andh2 as shown in the figure. If l is the length of horizontal arm of the tube, the acceleration a is
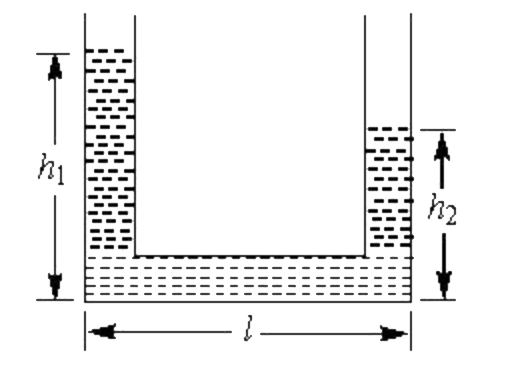 View Solution
View SolutionA wooden plank of length 1m and uniform cross-section is hinged at one end to the bottom of a tank as shown in fig. The tank is filled with water upto a hight 0.5m. The specific gravity of the plank is 0.5. Find the angle θ that the plank makes with the vertical in the equilibrium position. (Exclude the case θ=θ∘)
 View Solution
View SolutionA uniform rod of length L and weight WR is suspended as shown in the accompanying figure. A weight W is added to the end of the rod. The rod rests in horizontal position and is hinged at O. the support wire is at an angle θ to the rod. What is the tension T in the wire ?
 View Solution
View SolutionConsider a regular tank of size (l×b) filled with a liquid of density ρ to a height H as shown in figure. Find the force at the base and on the wall of the tank.
 View Solution
View SolutionA rod of length L, cross sectional area A and density ρ is hanging from a rigid support by spring of stiffries k. A very small sphere of mass m is rigidly attached at the bottom of the rod. The rod is partially immersed in a liquid of density ρ. Find the period of small oscillations.
View SolutionA uniform rod of length L and mass M is pivoted freely at one end and placed in vertical position.
a. What is angular acceleration of the rod when it is at ann angle θ with the vertical?
b. What is the tangential linear acceleration of the free end when the rod is horizontal?View Solution

